
- •Глава 3 Предельное значение функции. Непрерывность § 1. Предел функции
- •§ 2. Односторонние пределы функции
- •§ 3. Предел отношения синуса к своей дуге
- •§ 4. Число e
- •§ 5. Предел функции при
- •§ 6. Натуральные логарифмы. Показательная функция . Гиперболические функции
- •§ 7. Бесконечно малые и бесконечно большие функции
- •§ 8. Свойства конечных пределов, связанные с арифметическими действиями над функциями
- •§ 9. Сравнение бесконечно малых функций
- •§ 10. Непрерывность функций
- •§ 11. Свойства непрерывных функций
- •2. Арифметические операции над непрерывными функциями.
- •3. Непрерывность сложной функции.
- •§ 12. Непрерывность элементарных функций
- •§ 13. Свойства функций, непрерывных в замкнутом промежутке
- •§ 14. Понятие обратной функции
- •§ 15. Непрерывность элементарных функций (продолжение)
- •§ 16. Три важных предела
- •§ 17. Степенно-показательные выражения
- •§ 18. Теоремы Вейерштрасса
- •§ 19. Понятие равномерной непрерывности функции. Теорема Кантора
- •§ 20. Точки разрыва функций и их классификация
§ 14. Понятие обратной функции
Определение.
Функция
![]() ,
заданная на множестве
,
заданная на множестве
![]() ,
называется обратимой,
если неравным значениям аргумента
отвечают неравные же значения функции,
т. е. если
,
называется обратимой,
если неравным значениям аргумента
отвечают неравные же значения функции,
т. е. если
![]() ,
то и
,
то и
![]() .(Здесь
.(Здесь
![]() и
и
![]() — любые две точки из
— любые две точки из
![]() ).
).
Пусть функция
![]() — обратимая, заданная на множестве
— обратимая, заданная на множестве
![]() ,
и пусть
,
и пусть
![]() — множество всех значений этой функции.
— множество всех значений этой функции.
Возьмем любое
![]() .
Ясно, что на множестве
.
Ясно, что на множестве
![]() найдется одно
и только одно значение
найдется одно
и только одно значение
![]() такое, что
такое, что
![]() .
Таким образом, каждому значению
.
Таким образом, каждому значению
![]() из множества
из множества
![]() отвечает совершенно определенное
значение
отвечает совершенно определенное
значение
![]() (
(![]() и такое, что
и такое, что
![]() ).
Это означает, что
).
Это означает, что
![]() есть функция от
есть функция от
![]() ,
определенная на множестве
,
определенная на множестве
![]() ,
т. е.
,
т. е.
![]() ,
,
![]() .
Функция
.
Функция
![]() ,
определенная на множестве
,
определенная на множестве
![]() ,
называется обратной
функцией
для функции
,
называется обратной
функцией
для функции
![]() ,
определенной на множестве X.
,
определенной на множестве X.
Определение.
Пусть функция
![]() задана на промежутке X.
Если из неравенства:
задана на промежутке X.
Если из неравенства:
![]() ,
где
,
где
![]() и
и
![]() — любые две точки из
— любые две точки из
![]() ,
следует неравенство:
,
следует неравенство:
![]() ,
то функция
,
то функция
![]() называется строго
возрастающей
в промежутке X.
называется строго
возрастающей
в промежутке X.
Если же из
неравенства:
![]() ,
где
,
где
![]() и
и
![]() — любые две точки из
— любые две точки из
![]() ,
следует неравенство:
,
следует неравенство:
![]() ,
то функция
,
то функция
![]() называется строго
убывающей
в промежутке X.
называется строго
убывающей
в промежутке X.
Отметим, что функции строго возрастающие и строго убывающие являются обратимыми.
Теорема.
Пусть функция
![]() определена в промежутке
определена в промежутке
![]() (
(![]() )
и является там строго возрастающей и
непрерывной. Тогда у функции
)
и является там строго возрастающей и
непрерывной. Тогда у функции
![]() имеется обратная функция
имеется обратная функция
![]() ,
определенная в промежутке
,
определенная в промежутке
![]() ,
где
,
где
![]() ,
,
![]() ,
причем эта функция строго возрастающая
и непрерывная в промежутке
,
причем эта функция строго возрастающая
и непрерывная в промежутке
![]() .
.
► Функция
![]() строго возрастающая в
строго возрастающая в
![]() ,
следовательно, она обратима и потому у
нее существует обратная функция
,
следовательно, она обратима и потому у
нее существует обратная функция
![]() .
Как всегда, эта обратная функция
определена на множестве
.
Как всегда, эта обратная функция
определена на множестве
![]() ,
состоящем из всех значений функции
,
состоящем из всех значений функции
![]() .
.
1.
Покажем, что
![]() .
Для этого докажем, что: 1)
.
Для этого докажем, что: 1)
![]() и 2)
и 2) ![]() .
.
Пусть
![]() — любое, принадлежащее
— любое, принадлежащее
![]() (
(![]() ).
Это значит, что
).
Это значит, что
![]() — одно из значений, принимаемых функцией
— одно из значений, принимаемых функцией
![]() в промежутке
в промежутке
![]() .
Следовательно, в промежутке
.
Следовательно, в промежутке
![]() имеется
имеется
![]() такое, что
такое, что
![]() .
.
Так как
![]() и так как функция
и так как функция
![]() строго возрастающая, то
строго возрастающая, то
![]() ,
т. е.
,
т. е.
![]() ,
а значит,
,
а значит,
![]() .
.
Итак, из того, что
![]() ,
следует:
,
следует:
![]() .
Так как
.
Так как
![]() — любой элемент из
— любой элемент из
![]() ,
то заключаем, что
,
то заключаем, что
![]() .
(*)
.
(*)
Пусть теперь
![]() — любое, принадлежащее
— любое, принадлежащее
![]() (
(![]() ).
Покажем, что
).
Покажем, что
![]() .
Для этого надо показать, что в промежутке
.
Для этого надо показать, что в промежутке
![]() обязательно найдется
обязательно найдется
![]() такое, что
такое, что
![]() .
Если
.
Если
![]() (у нас
(у нас
![]() ),
то таким
),
то таким
![]() является
является
![]() .
Если
.
Если
![]() (у нас
(у нас
![]() ),
то таким
),
то таким
![]() является
является
![]() .
Если же
.
Если же
![]() ,
то существование требуемого
,
то существование требуемого
![]() в промежутке
в промежутке
![]() вытекает из второй теоремы Больцано-Коши.
вытекает из второй теоремы Больцано-Коши.
Итак, из того, что
![]() ,
следует, что
,
следует, что
![]() .
Так как
.
Так как
![]() — любой элемент из
— любой элемент из
![]() ,
то это означает, что
,
то это означает, что
![]() .
(**)
.
(**)
Из того, что
![]() и
и
![]() следует, что
следует, что
![]() .
.
2.
Покажем теперь, что функция
![]() строго возрастает в
строго возрастает в
![]() .
Для этого в промежутке
.
Для этого в промежутке
![]() возьмем
возьмем
![]() и
и
![]() — любые, но такие, что
— любые, но такие, что
![]() .
Положим
.
Положим
![]() ,
,
![]() .
Ясно, что
.
Ясно, что
![]() и
и
![]() и что
и что
![]() ,
,
![]() .
Так как
.
Так как
![]() и
и
![]() — вещественные числа, то, по свойству
упорядоченности системы W,
обязательно имеет место одно и только
одно из трех соотношений:
— вещественные числа, то, по свойству
упорядоченности системы W,
обязательно имеет место одно и только
одно из трех соотношений:
![]() .
.
Если бы было:
![]() ,
то тогда оказалось бы:
,
то тогда оказалось бы:
![]() ,
т. е.
,
т. е.
![]() ,
а это не так. Значит, соотношение
,
а это не так. Значит, соотношение
![]() исключается. Если бы было:
исключается. Если бы было:
![]() ,
то тогда оказалось бы:
,
то тогда оказалось бы:
![]() ,
т. е.
,
т. е.
![]() ,
а это не так. Значит, соотношение
,
а это не так. Значит, соотношение
![]() исключается. Так как соотношения
исключается. Так как соотношения
![]() и
и
![]() исключены, то остается только соотношение
исключены, то остается только соотношение
![]() ,
а значит,
,
а значит,
![]() .
Таким образом, получили: из того, что
.
Таким образом, получили: из того, что
![]() ,
где
,
где
![]() и
и
![]() — любые две точки из
— любые две точки из
![]() ,
следует, что
,
следует, что
![]() .
А это означает, что функция
.
А это означает, что функция
![]() — строго возрастающая в
— строго возрастающая в
![]() .
.
3.
Остается доказать непрерывность функции
![]() в
в
![]() .
Возьмем любую точку
.
Возьмем любую точку
![]() и установим непрерывность функции
и установим непрерывность функции
![]() в этой точке. Тем самым будет установлена
непрерывность функции
в этой точке. Тем самым будет установлена
непрерывность функции
![]() в промежутке
в промежутке
![]() .
.
Пусть для
определенности:
![]() .
Положим
.
Положим
![]() (
(![]() ).
Возьмем
).
Возьмем
![]() — любое, но такое, чтобы было:
— любое, но такое, чтобы было:
![]() и
и
![]()
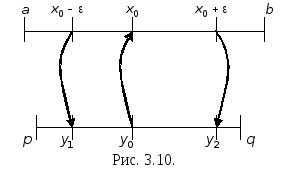 .
Положим
.
Положим
![]() ,
,
![]() .
Ясно, что точки
.
Ясно, что точки
![]() и
и
![]() .
Пусть
.
Пусть
![]() ,
,
![]() .
Ясно, что точки
.
Ясно, что точки
![]() и
и
![]() принадлежат
принадлежат
![]() и
и
![]() (см. рис. 3.10).
(см. рис. 3.10).
Возьмем
![]() — любое, удовлетворяющее неравенству:
— любое, удовлетворяющее неравенству:
![]() (4)
(4)
Так как функция
![]() — строго возрастающая, то из неравенства
(4) вытекает неравенство
— строго возрастающая, то из неравенства
(4) вытекает неравенство
![]() ,
(5)
,
(5)
т. е.
![]()
![]()
![]() .
.
Подчеркнем еще
раз, что неравенство
![]() е выполняется для всех
е выполняется для всех
![]() ,
удовлетворяющих неравенству:
,
удовлетворяющих неравенству:
![]() .
Заметив это, положим
.
Заметив это, положим
![]() .
Ясно, что
.
Ясно, что
![]() ,
ибо разности
,
ибо разности
![]() и
и
![]() положительные. А тогда всякое
положительные. А тогда всякое
![]() ,
удовлетворяющее условию
,
удовлетворяющее условию
![]() ,
будет удовлетворять неравенству (4) и,
следовательно, для всякого
,
будет удовлетворять неравенству (4) и,
следовательно, для всякого
![]() ,
удовлетворяющего условию
,
удовлетворяющего условию
![]() ,
будет:
,
будет:
![]() .
А это означает,
что функция
.
А это означает,
что функция
![]() непрерывна в точке
непрерывна в точке
![]() .
◄
.
◄
Замечание 1. Аналогичная теорема имеет место для строго убывающих функций. Именно.
Пусть функция
![]() определена в промежутке
определена в промежутке
![]() (
(![]() )
и является там строго убывающей и
непрерывной. Тогда у функции
)
и является там строго убывающей и
непрерывной. Тогда у функции
![]() имеется обратная функция
имеется обратная функция
![]() ,
определенная в промежутке
,
определенная в промежутке
![]() ,
где
,
где
![]() ,
,
![]() ,
причем эта функция строго убывающая и
непрерывная в промежутке
,
причем эта функция строго убывающая и
непрерывная в промежутке
![]() .
.
Замечание 2. Справедливы также следующие утверждения.
I.
Пусть функция
![]() определена в промежутке
определена в промежутке
![]() (
(![]() )
и является там строго возрастающей и
непрерывной. Тогда у функции
)
и является там строго возрастающей и
непрерывной. Тогда у функции
![]() имеется обратная функция
имеется обратная функция
![]() ,
определенная в промежутке
,
определенная в промежутке
![]() ,
где
,
где
![]() ,
,
![]() ,
причем эта функция строго возрастающая
и непрерывная в промежутке
,
причем эта функция строго возрастающая
и непрерывная в промежутке
![]() .
.
II.
Пусть функция
![]() определена в промежутке
определена в промежутке
![]() (
(![]() )
и является там строго убывающей и
непрерывной. Тогда у функции
)
и является там строго убывающей и
непрерывной. Тогда у функции
![]() имеется обратная функция
имеется обратная функция
![]() ,
определенная в промежутке
,
определенная в промежутке
![]() ,
где
,
где
![]() ,
,
![]() ,
причем эта функция строго возрастающая
и непрерывная в промежутке
,
причем эта функция строго возрастающая
и непрерывная в промежутке
![]() .
.
Заметим, что
некоторые из чисел
![]() могут быть несобственными.
могут быть несобственными.
