§ 15. Непрерывность элементарных функций (продолжение)

1. .

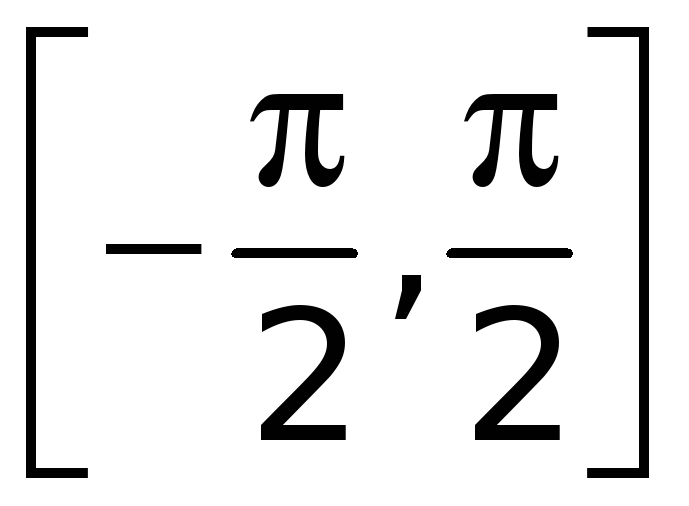Рассмотрим функцию . Эта функция определена и непрерывна на всей оси, а на промежутке она еще и строго возрастающая. значит, рассматривая ее для 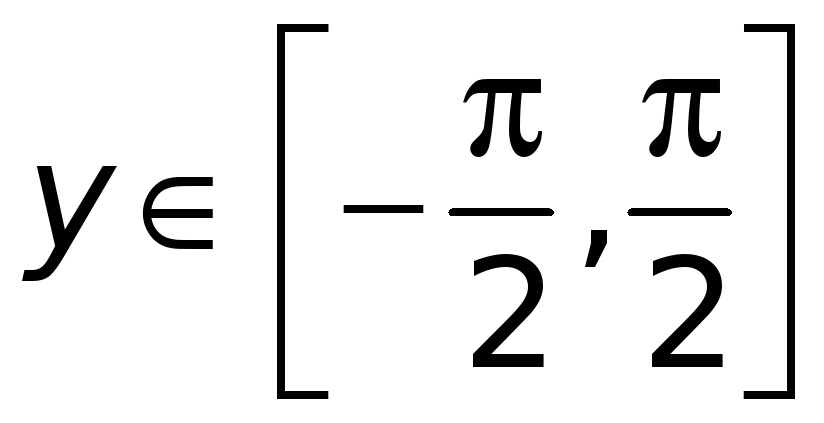мы можем применить к ней теорему об обратной функции. По теореме об обратной функции, функция будет определена на промежутке и будет строго возрастающей и непрерывной на этом промежутке.

2. .

Рассмотрим функцию . Эта функция определена и непрерывна на всей оси, а на промежутке она еще и строго убывающая. Значит, рассматривая ее для , мы можем применить к ней теорему об обратной функции. По теореме об обратной функции, функция будет определена на промежутке и будет строго убывающей и непрерывной на этом промежутке.

3. .

Рассмотрим функцию . Эта функция определена на промежутке , строго возрастает и непрерывна там. Имеем , . Рассматривая функцию для 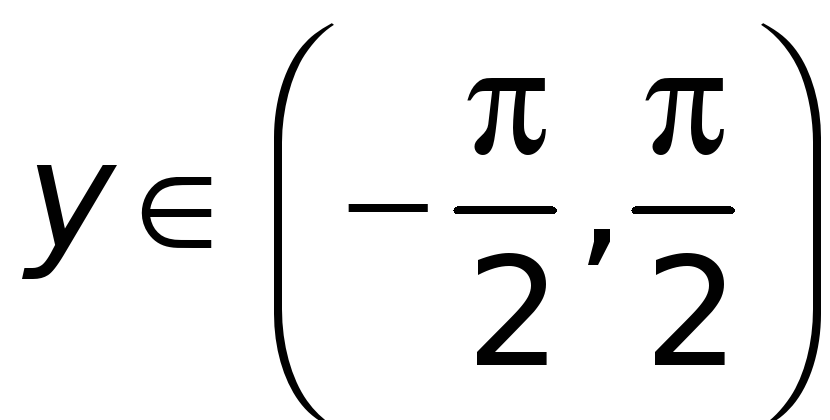, приходим к выводу, что функция определена в промежутке , строго возрастает и непрерывна на этом промежутке.

4. .

Рассмотрим функцию . Эта функция на промежутке определена, строго убывает и непрерывна. Имеем , . Рассматривая функцию для , приходим к выводу, что функция определена в промежутке , строго убывает и непрерывна на этом промежутке.

5. Логарифмическая функция (). Логарифмическая функция является обратной для показательной функции: , .

α) Пусть . В этом случае функция — строго возрастающая и непрерывная в промежутке . Имеем ; . Следовательно, если , то функция определена в промежутке , строго возрастающая и непрерывная в этом промежутке.

β) Пусть . В этом случае функция — строго убывающая и непрерывная в промежутке . Имеем , . Следовательно, если , то функция определена в промежутке , строго убывающая и непрерывная в этом промежутке.

6. Общая степенная функция , где — любое вещественное число ().

В качестве определения общей степенной функции при любом вещественном и принимаем выражение: , . Имеем , где . Видим, что функция , , — любое вещественное число, будет непрерывна на промежутке как суперпозиция непрерывных функций.

Итак, мы рассмотрели основные (простейшие) элементарные функции и показали, что каждая простейшая элементарная функция непрерывна в каждой точке области своего существования.

Введем понятие класса элементарных функций. К классу элементарных функций относят прежде всего основные (простейшие) элементарные функции, а также все функции, получающиеся из основных с помощью первых четырех арифметических действий и операций суперпозиций, последовательно примененных конечное число раз.

Было установлено выше, что любая арифметическая операция над непрерывными функциями приводит к функции, непрерывной в каждой точке области ее существования. Было установлено также, что суперпозиция непрерывных функций есть функция непрерывная. Поэтому можно сделать общий вывод: всякая элементарная функция непрерывна в каждой точке области своего существования.

§ 16. Три важных предела

1. Предел функци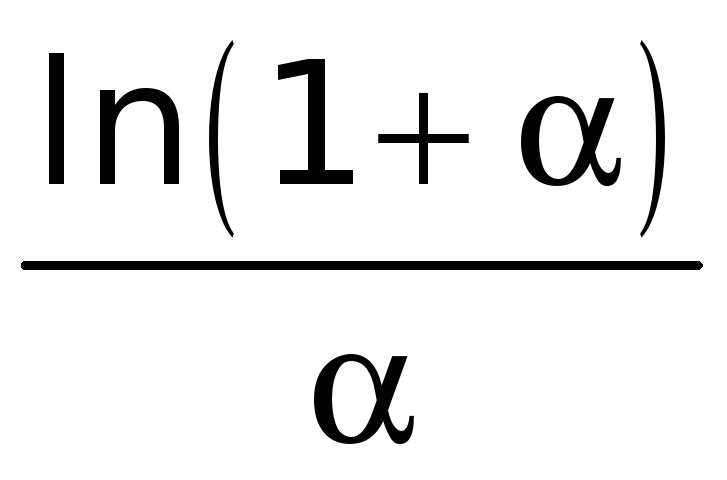и при .

Установим, что .

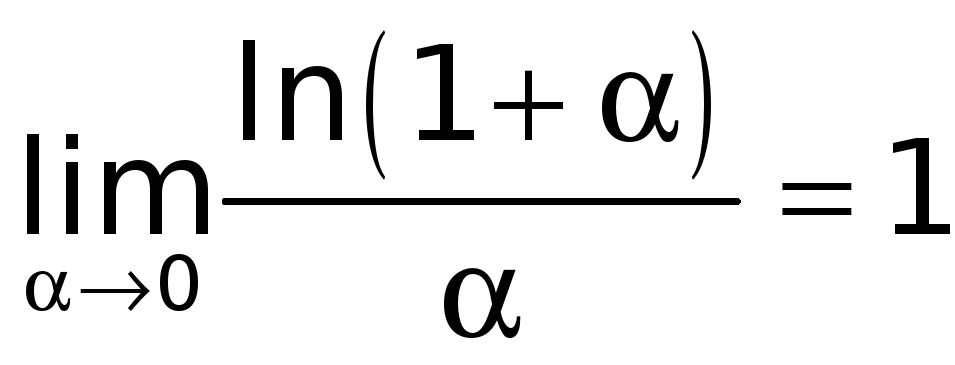► Имеем 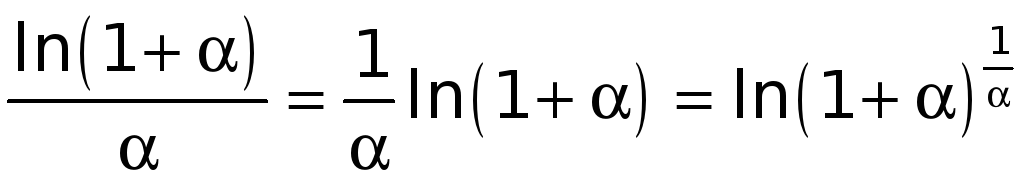. Перейдем в этом равенстве к пределу при . Так как логарифмическая функция есть функция непрерывная, то 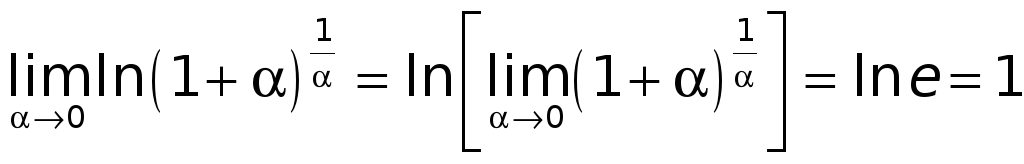. Следовательно,

. ◄

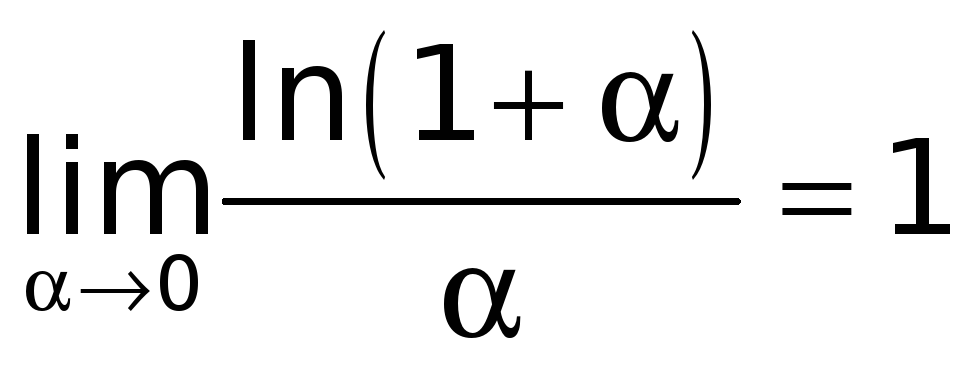2. Предел функци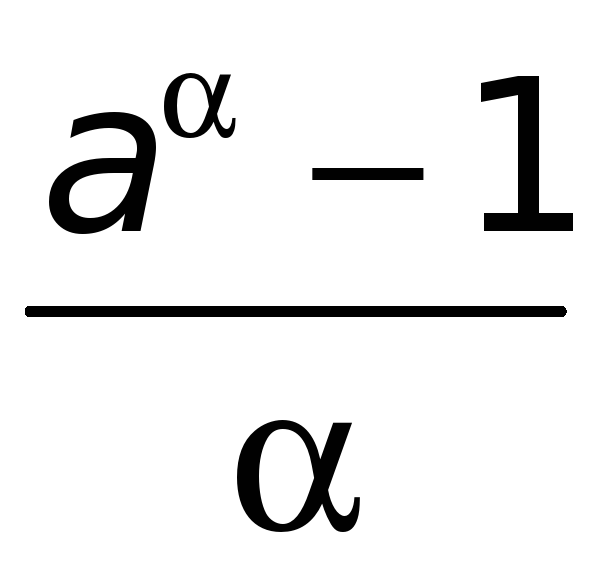и при .

Установим, что .

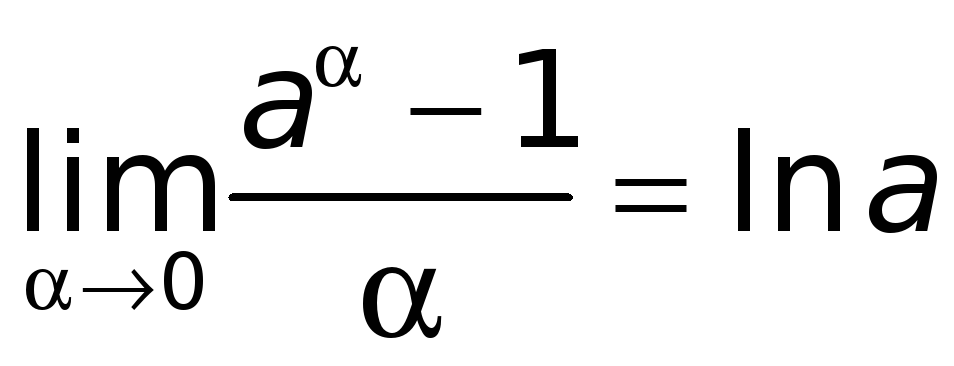► Положим

. (6)

Заметим, что , если (ибо ). Из равенства (6) находим . Имеем .

Перейдем в этом равенстве к пределу при . Будем иметь

. ◄

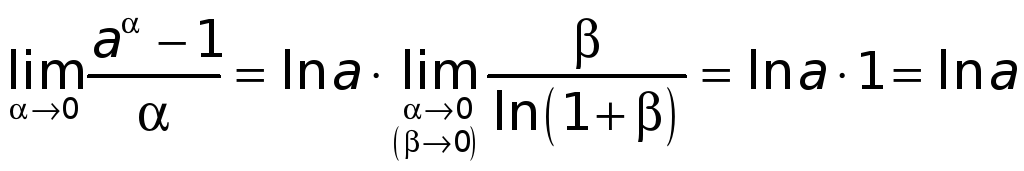3. Предел функци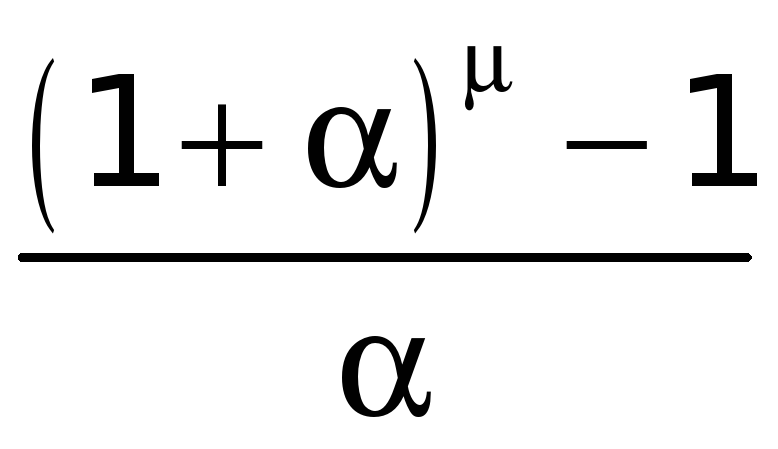и при .

Установим, что .

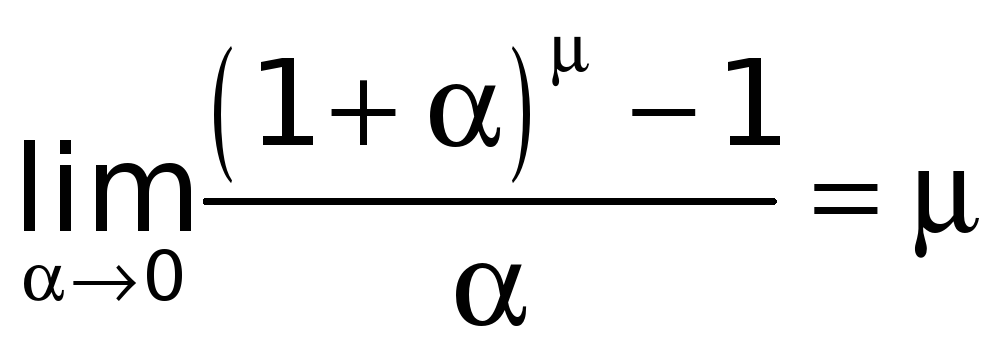► Положим

. (7)

Заметим, что , если (ибо ). Имеем

.

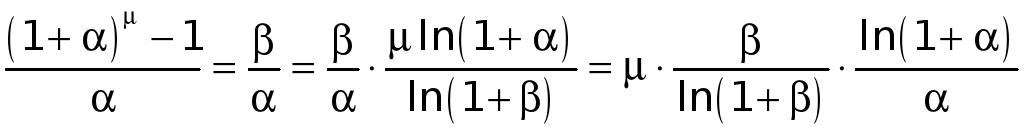Перейдем в этом равенстве к пределу при (а, следовательно, и ). Получим

. ◄
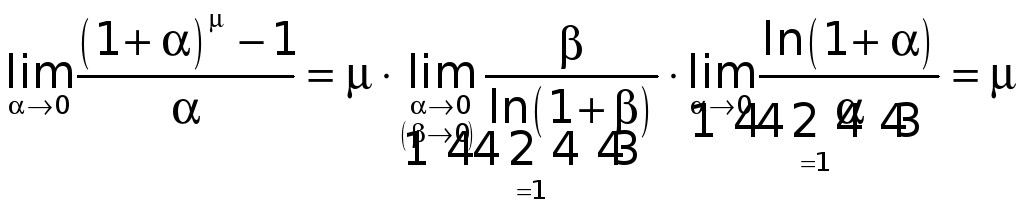