§ 10. Непрерывность функций

Станем рассматривать функцию , определенную на некотором множестве , и точку . Точка и обладает свойством: в любой окрестности точки имеются точки множества X, отличные от .

Отметим, что, так как точка принадлежит области определения функции, то в этой точке функция имеет определенное значение . Дадим определение непрерывности функции в точке следующими равносильными способами.

I. Функция называется непрерывной в точке , если

. (1)

Так как , то равенству (1) можно придать такую форму:

,

что кратко выражают словами: предел функции равен значению функции от предела аргумента.

II. Функция называется непрерывной в точке , если для любой последовательности значений аргумента : такой, что и , оказывается, что соответствующая последовательность значений функции: сходится к . Обращаем внимание на тот факт, что здесь нет запрета: .

III. Функция называется непрерывной в точке , если любому, сколь угодно малому, отвечает число такое, что как только и , так сейчас же . (Здесь нет запрета: .)

Замечание 1. Пусть , и пусть . Величина называется приращением независимой переменной. Отметим, что может быть больше нуля, а может быть и меньше нуля.

Пусть , . Величина

называется приращением функции в точке , соответствующим приращению аргумента (отметим, что может быть больше нуля, а может быть и меньше нуля и даже равно нулю).

Предположим теперь, что функция непрерывна в точке . Это означает, что , или , или . Следовательно, можно сказать: функция будет непрерывной в точке тогда и только тогда, когда бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции .

Замечание 2. Подобно тому как определялись правосторонние и левосторонние пределы функции в некоторой точке , можно определить правостороннюю и левостороннюю непрерывность функции в точке .

Определение. 1) Функция называется непрерывной справа в точке , если .

2) Функция называется непрерывной слева в точке , если .

Отметим, что если функция непрерывна в точке в обычном смысле, то она непрерывна в этой точке одновременно и справа, и слева; если функция непрерывна в точке одновременно и справа и слева, то она непрерывна в этой точке и в обычном смысле.

Замечание 3. Пусть функция определена в замкнутом промежутке . Говорят, что функция непрерывна в замкнутом промежутке , если она непрерывна в обычном смысле в каждой внутренней точке этого промежутка и если она непрерывна справа в точке и непрерывна слева в точке .

Замечание 4. В дальнейшем будем рассматривать, как правило, функции, для которых областью определения является промежуток. В этом случае любая точка обладает свойством: в любой окрестности точки имеются точки множества , отличные от точки .

§ 11. Свойства непрерывных функций

1. Теорема (о стабильности знака). Пусть функция определена в промежутке и точка . Если и непрерывна в точке , то существует такое, что для всех из , удовлетворяющих неравенству , будет: .

► Положим ( по условию). Так как непрерывна в точке , то любому (в частности ) отвечает число такое, что как только и , так сейчас же . В частности,

,

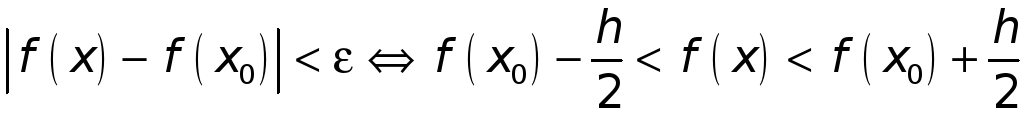откуда .

Таким образом, получено: для и удовлетворяющих неравенству , будет . ◄

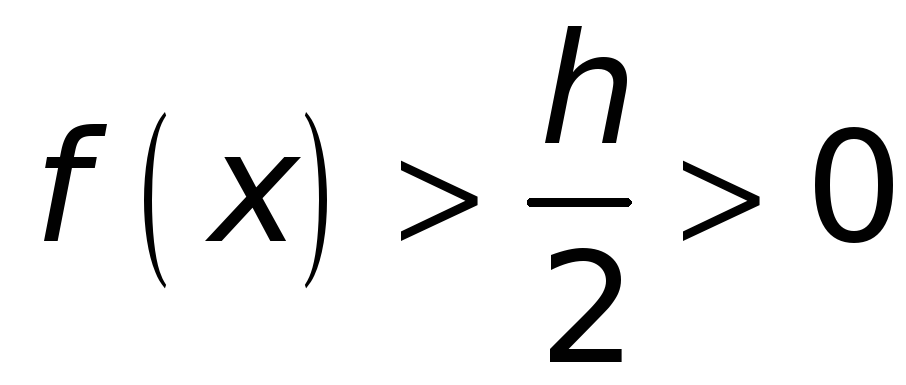Замечание. Справедливо также утверждение: если и непрерывна в точке , то существует такое, что для всех из , удовлетворяющих неравенству , будет: .