- •Глава 3 Предельное значение функции. Непрерывность § 1. Предел функции
- •§ 2. Односторонние пределы функции
- •§ 3. Предел отношения синуса к своей дуге
- •§ 4. Число e
- •§ 5. Предел функции при
- •§ 6. Натуральные логарифмы. Показательная функция . Гиперболические функции
- •§ 7. Бесконечно малые и бесконечно большие функции
- •§ 8. Свойства конечных пределов, связанные с арифметическими действиями над функциями
- •§ 9. Сравнение бесконечно малых функций
- •§ 10. Непрерывность функций
- •§ 11. Свойства непрерывных функций
- •2. Арифметические операции над непрерывными функциями.
- •3. Непрерывность сложной функции.
- •§ 12. Непрерывность элементарных функций
- •§ 13. Свойства функций, непрерывных в замкнутом промежутке
- •§ 14. Понятие обратной функции
- •§ 15. Непрерывность элементарных функций (продолжение)
- •§ 16. Три важных предела
- •§ 17. Степенно-показательные выражения
- •§ 18. Теоремы Вейерштрасса
- •§ 19. Понятие равномерной непрерывности функции. Теорема Кантора
- •§ 20. Точки разрыва функций и их классификация
§ 2. Односторонние пределы функции
Пусть а и А — конечные числа.
Определение.
Число А
называют правым
пределом
функции
![]() при
при
![]() и пишут:
и пишут:
![]() или
или
![]() ,
если для любого, сколь угодно малого,
числа
,
если для любого, сколь угодно малого,
числа
![]() можно указать число
можно указать число
![]() такое, что как только
такое, что как только
![]() и
и
![]() ,
так сейчас же
,
так сейчас же
![]() (т. е. для всех
(т. е. для всех
![]() оказывается
оказывается
![]() ;
здесь
;
здесь
![]() — правая полуокрестность точки а).
— правая полуокрестность точки а).
Определение.
Число А
называют левым
пределом
функции
![]() при
при
![]() и пишут:
и пишут:
![]() или
или
![]() ,
если для любого, сколь угодно малого,
числа
,
если для любого, сколь угодно малого,
числа
![]() можно указать число
можно указать число
![]() такое, что как только
такое, что как только
![]() и
и
![]() ,
так сейчас же
,
так сейчас же
![]() (т. е. для всех
(т. е. для всех
![]() оказывается
оказывается
![]() ;
здесь
;
здесь
![]() — левая полуокрестность точки а).
— левая полуокрестность точки а).
Замечание 1. Справедливы утверждения:
1) если у функции
![]() при
при
![]() существует предел А
в обычном смысле, т. е. двусторонний, то
существуют оба односторонних предела:
существует предел А
в обычном смысле, т. е. двусторонний, то
существуют оба односторонних предела:
![]() и
и
![]() ,
причем оба они равны А;
,
причем оба они равны А;
2) если у функции
![]() при
при
![]() существуют оба односторонних предела:
существуют оба односторонних предела:
![]() и
и
![]() и оба они равны числу А,
то у
и оба они равны числу А,
то у
![]() при
при
![]() существует двусторонний предел, равный
указанным односторонним пределам, т.
е. числу А.
существует двусторонний предел, равный
указанным односторонним пределам, т.
е. числу А.
В качестве упражнения утверждения 1) и 2) предлагается доказать самостоятельно.
Замечание 2.
В определении односторонних пределов
функции
![]() при
при
![]() число А
предполагалось конечным. Отметим, что
А
может быть и числом несобственным:
число А
предполагалось конечным. Отметим, что
А
может быть и числом несобственным:
![]() или
или
![]() .
.
§ 3. Предел отношения синуса к своей дуге
Установим, что
![]() .
(1)
.
(1)
► Так как
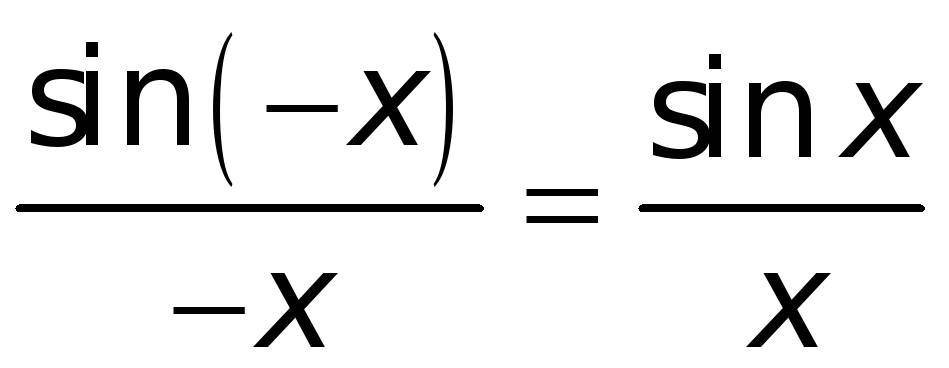 ,
то
,
то
![]() ,
если эти пределы существуют.Поэтому,
чтобы установить (1), достаточно доказать,
что существует и равен 1 хотя бы один
односторонний предел функции
,
если эти пределы существуют.Поэтому,
чтобы установить (1), достаточно доказать,
что существует и равен 1 хотя бы один
односторонний предел функции
![]() при
при
![]() ,
например, правый, т. е. достаточно
доказать, что
,
например, правый, т. е. достаточно
доказать, что
![]() .
(2)
.
(2)
Так как мы станем
устанавливать справедливость соотношения
(2), то можно рассматривать лишь значения
![]() ,
удовлетворяющие неравенству:
,
удовлетворяющие неравенству:
![]() .
В круге радиуса
.
В круге радиуса
![]() рассмотрим угол
рассмотрим угол
![]() ,
радианная мера которого
,
радианная мера которого
![]()
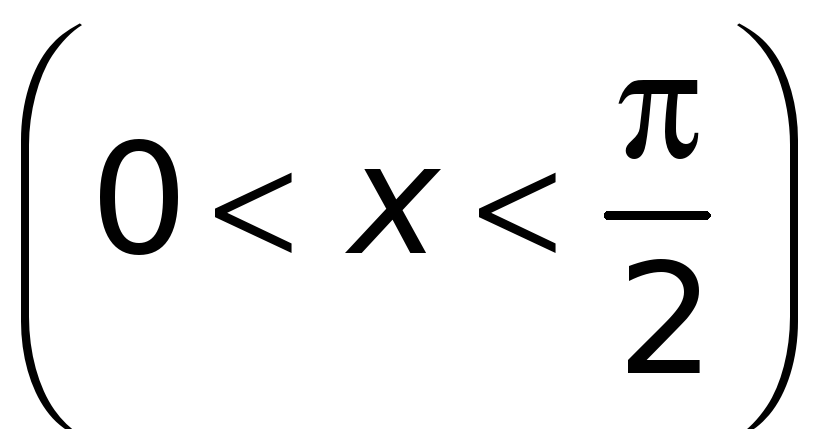 ;
хорду
;
хорду
![]() и касательную
и касательную
![]() к окружности в точке А
(см. рис. 3.1). Имеем очевидные неравенства:
площадь
к окружности в точке А
(см. рис. 3.1). Имеем очевидные неравенства:
площадь
![]() < площади сектора
< площади сектора
![]() < площади
< площади
![]() (при этом мы пользуемся теми сведениями
о площадях элементарных фигур, которые
известны из школьного курса), или
(при этом мы пользуемся теми сведениями
о площадях элементарных фигур, которые
известны из школьного курса), или
![]() ,
,
откуда
 .
(3)
.
(3)
|
Рис. 3.1. К выводу формулы (1) |
![]() .
.
Вычитая из 1 каждый из членов последнего неравенства, будем иметь
![]() .
(4)
.
(4)
Но
![]() (в силу(3)). Следовательно, вместо
неравенства (4) будем иметь
(в силу(3)). Следовательно, вместо
неравенства (4) будем иметь
![]() .
(5)
.
(5)
Возьмем
![]() — любое, сколь угодно малое (можно
считать, что
— любое, сколь угодно малое (можно
считать, что
![]() ).
Ясно, что если положить
).
Ясно, что если положить
![]() (
(![]() ),
то для всех
),
то для всех
![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
![]() ,
будет
,
будет
![]() ,
,
ибо если
![]() ,
то
,
то
![]() .
Значит,
.
Значит,
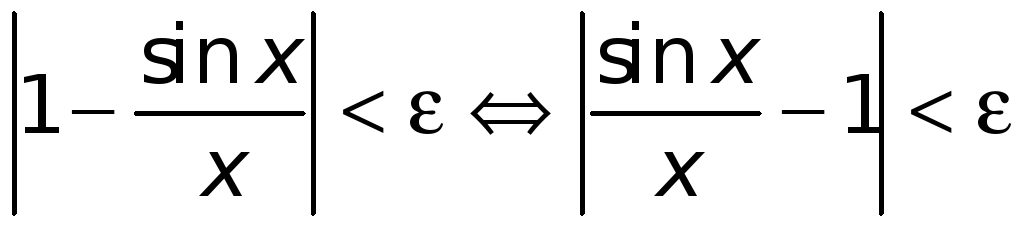 ,
если
,
если
![]() .
Последнее означает, что
.
Последнее означает, что
![]() .
Видим, что соотношение (2)
установлено, а значит, доказано и
соотношение (1). ◄
.
Видим, что соотношение (2)
установлено, а значит, доказано и
соотношение (1). ◄
§ 4. Число e
Определение. Числом е называется предел переменной
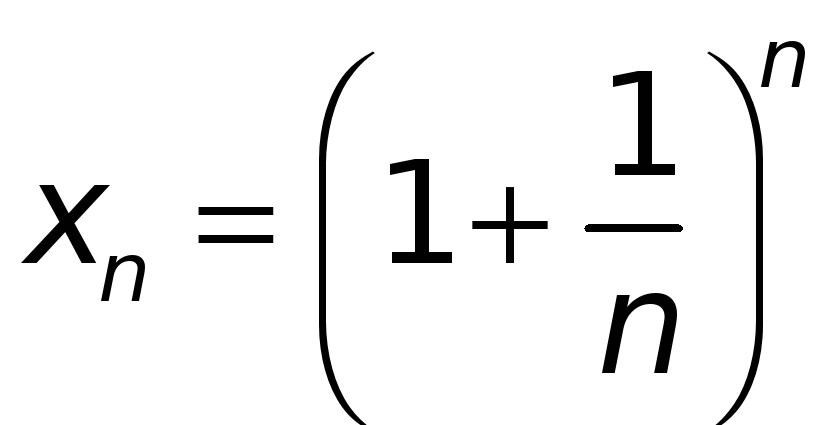
при
![]() натуральном, стремящемся к бесконечности.
натуральном, стремящемся к бесконечности.
Чтобы оправдать
это определение, надо установить, что
у переменной
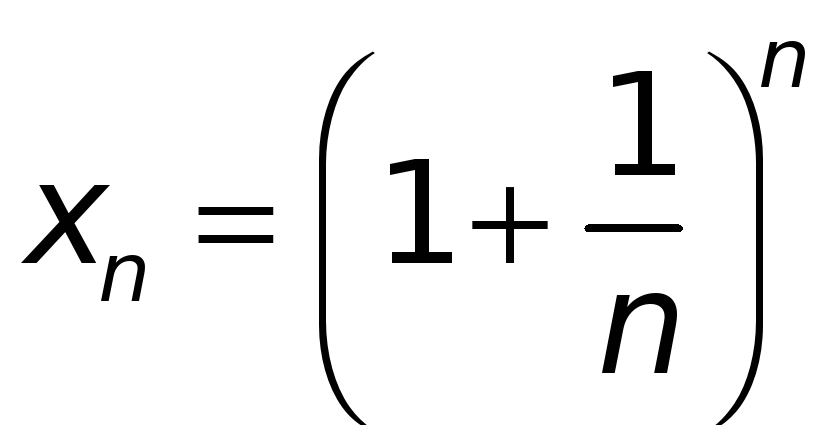 существует конечный предел при
существует конечный предел при
![]() .
Мы установим, что
.
Мы установим, что
![]() существует, конечный, если покажем, что
переменная
существует, конечный, если покажем, что
переменная
![]() — возрастающая и ограниченная сверху.
— возрастающая и ограниченная сверху.
► 1.
Покажем, что переменная
![]() — возрастающая.
— возрастающая.
Применяя формулу
бинома Ньютона,
![]() -й
член последовательности
-й
член последовательности
![]() можно написать в виде
можно написать в виде


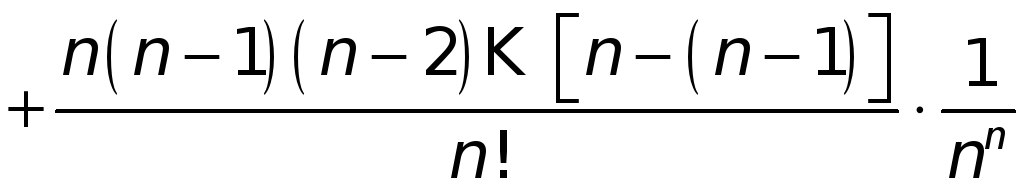 ,
,
или
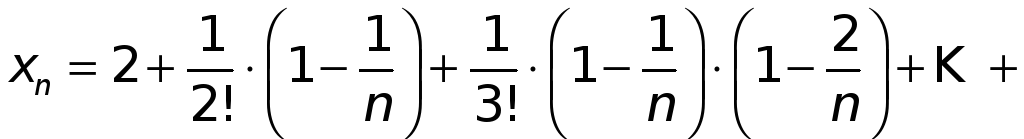

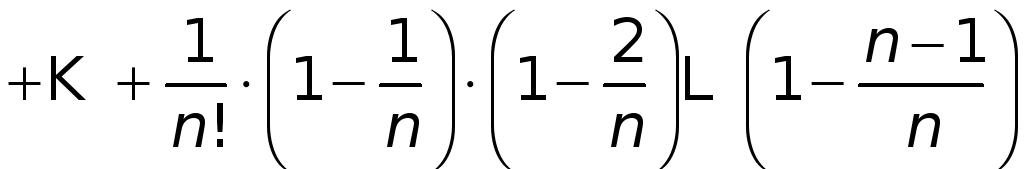 .
(2)
.
(2)
Аналогично, для
![]() -го
члена последовательности
-го
члена последовательности
![]() находим
находим
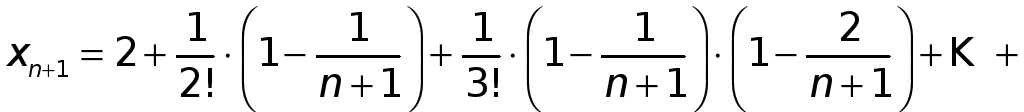
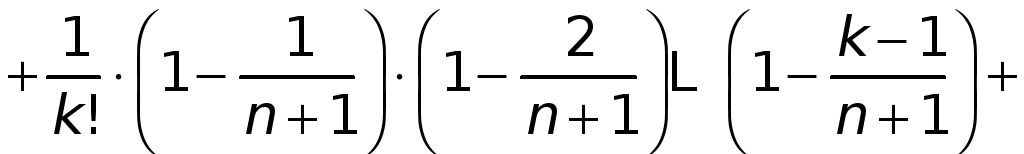
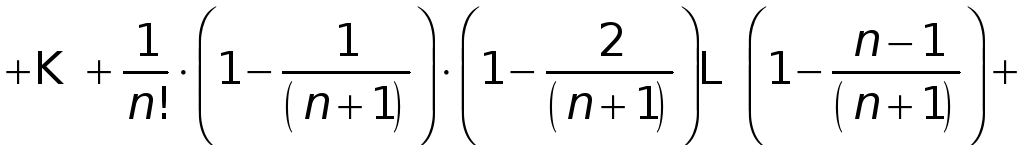
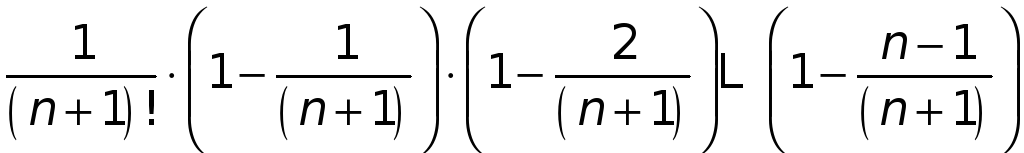 .
(3)
.
(3)
Заметим, что правая
часть соотношения (2) имеет
![]() слагаемых, а правая часть (3) имеет
слагаемых, а правая часть (3) имеет
![]() слагаемых.
слагаемых.
Сравнивая
![]() и
и
![]() ,
видим, что первые слагаемые в правых
частях (2) и (30 одинаковы, второе, третье
и т д.
,
видим, что первые слагаемые в правых
частях (2) и (30 одинаковы, второе, третье
и т д.
![]() -е
слагаемое у
-е
слагаемое у
![]() больше, чем у
больше, чем у
![]() ,
ибо
,
ибо
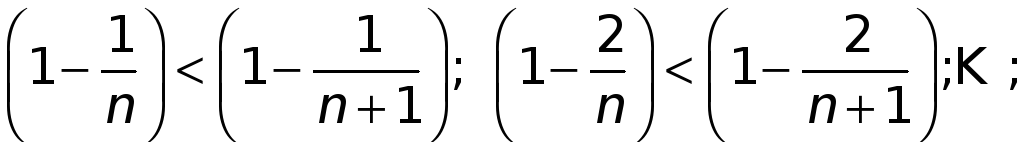
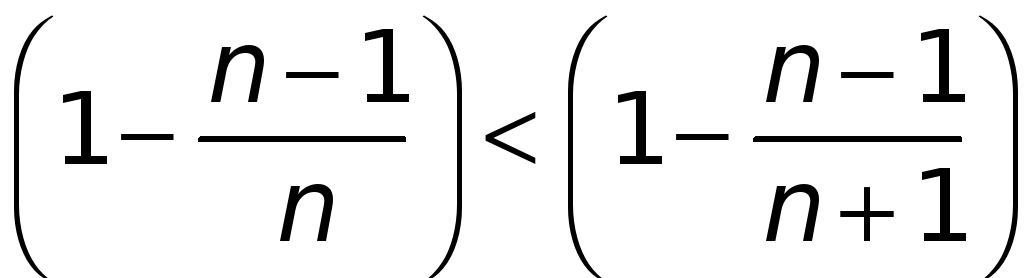 .
.
Кроме того, в
составе
![]() имеется еще
имеется еще
![]() -е
слагаемое, которого в составе
-е
слагаемое, которого в составе
![]() нет и которое является числом положительным.
Значит
нет и которое является числом положительным.
Значит
![]() ,
для любого
,
для любого
![]() ,
и, следовательно, переменная
,
и, следовательно, переменная
![]() — возрастающая.
— возрастающая.
2.
Покажем теперь, что переменная
![]() ограничена сверху. Для этого снова
воспользуемся формулой (2). Заменим все
разности, стоящие в скобках в правой
части этой формулы, на единицы, отчего
правая часть увеличится (ведь каждая
такая разность меньше единицы). Получим
ограничена сверху. Для этого снова
воспользуемся формулой (2). Заменим все
разности, стоящие в скобках в правой
части этой формулы, на единицы, отчего
правая часть увеличится (ведь каждая
такая разность меньше единицы). Получим
![]() .
.
Но
![]()
![]() .
.
Поэтому и подавно
![]() .
.
Так как
![]() ,
,
то получаем
![]() ,
для любого
,
для любого
![]() ,
т. е. переменная
,
т. е. переменная
![]() ограничена сверху. (Из формулы (2) видно,
что
ограничена сверху. (Из формулы (2) видно,
что
![]() и, следовательно,
и, следовательно,
![]() при всех
при всех
![]() .)
.)
Итак, показано,
что переменная
![]() монотонно
возрастает и ограничена сверху. Поэтому
существует конечный
монотонно
возрастает и ограничена сверху. Поэтому
существует конечный
![]() ,
величина которого заключена между
числами 2 и 3. Этот предел обозначается
буквой e.
◄
,
величина которого заключена между
числами 2 и 3. Этот предел обозначается
буквой e.
◄
Число е играет большую роль в математическом анализе и его приложениях. Доказано, что е — число иррациональное. Имеются приемы, позволяющие вычислить любое число знаков в его представлении бесконечной десятичной дробью. При этом установлено, что
е = 2,718281828459045... .
Рассмотрим теперь
переменную
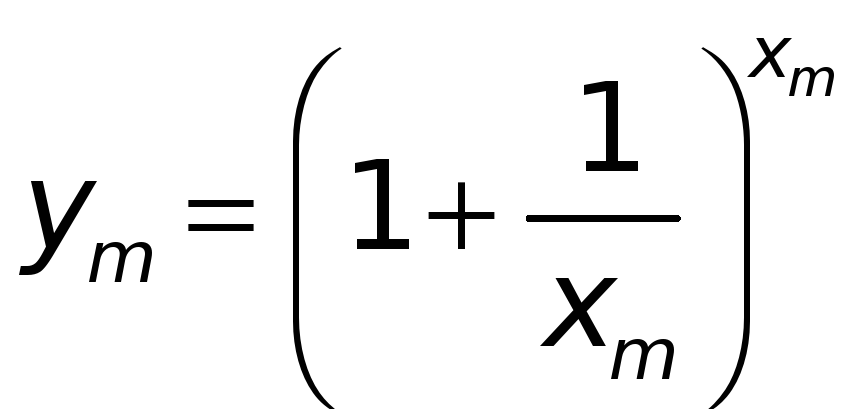 ,
где
,
где
![]() — положительные числа, большие 2 (
— положительные числа, большие 2 (![]() — не обязательно целые).
— не обязательно целые).
Справедливо
утверждение:
если
![]() ,
то
,
то
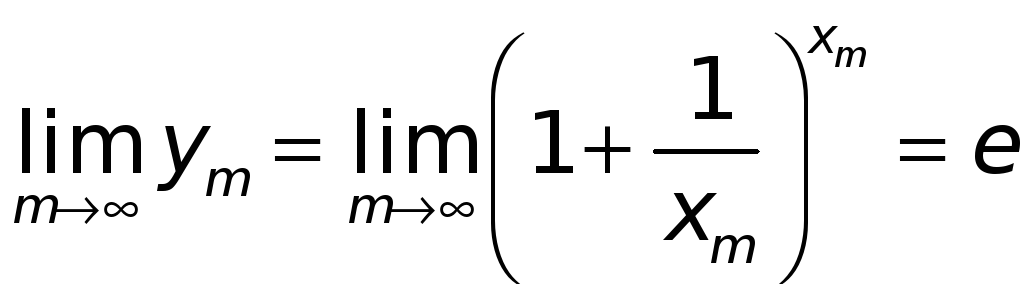 .
.
► 1.
Рассмотрим сначала случай, когда все
значения переменной
![]() являются целыми положительными числами.
Возьмем
являются целыми положительными числами.
Возьмем
![]() — любое, сколь угодно малое.
— любое, сколь угодно малое.
Мы знаем, что
 .
Значит, взятому
.
Значит, взятому
![]() отвечает номер
отвечает номер
![]() такой, что для всех
такой, что для всех
![]() будет
будет
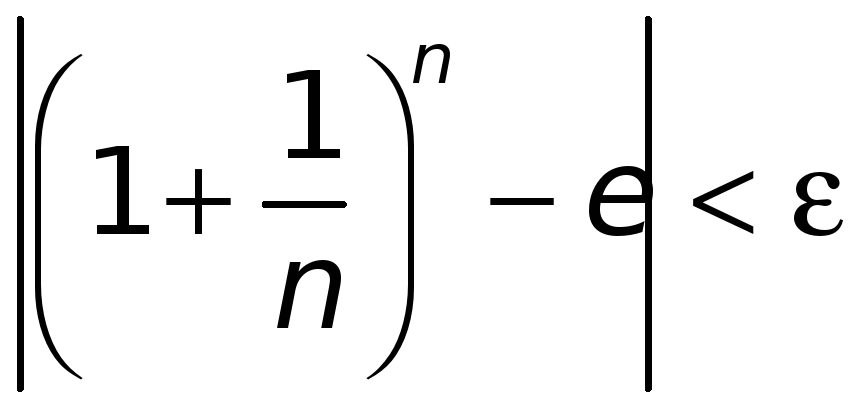 .
.
По условию
![]() .
Поэтому можно утверждать, что, начиная
с некоторого места, т. е. при
.
Поэтому можно утверждать, что, начиная
с некоторого места, т. е. при
![]() (
(![]() )
будет:
)
будет:
![]() .
У нас, по предположению, все значения
переменной
.
У нас, по предположению, все значения
переменной
![]() — целые положительные числа. Поэтому
при всех
— целые положительные числа. Поэтому
при всех
![]() будет иметь место неравенство
будет иметь место неравенство
 .
.
А это означает,
что
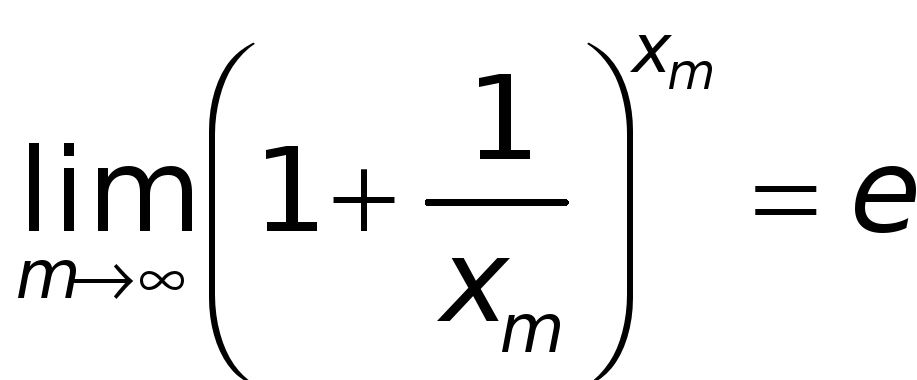 .
.
Отметим, что даже
в рассмотренном случае переменная
![]() не обязательно монотонно возрастающая.
не обязательно монотонно возрастающая.
2.
Пусть теперь значения переменной
![]() — положительные числа, большие 2, не
обязательно целые.
— положительные числа, большие 2, не
обязательно целые.
Пусть
![]() (
(![]() — наибольшее натуральное число,
удовлетворяющее неравенству:
— наибольшее натуральное число,
удовлетворяющее неравенству:
![]() ).
Ясно, что
).
Ясно, что
![]() ;
;
![]() ,
если
,
если
![]() .
Имеем
.
Имеем
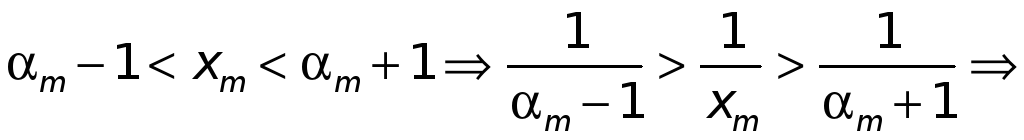
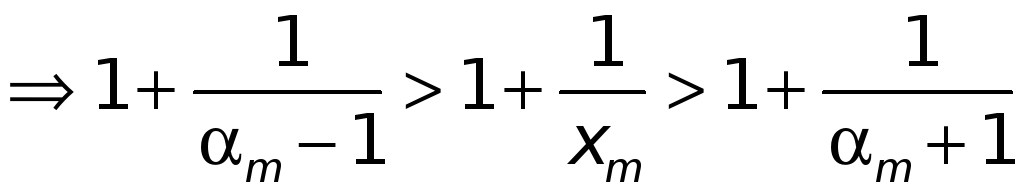 .
.
А тогда
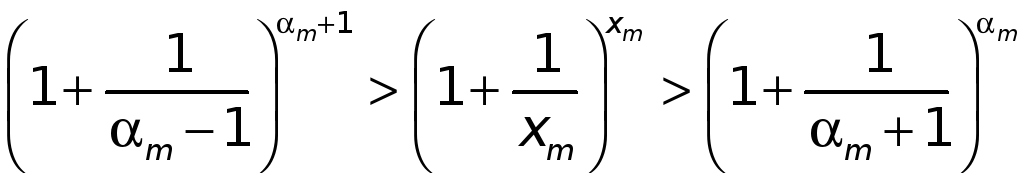 (4)
(4)
Имеем
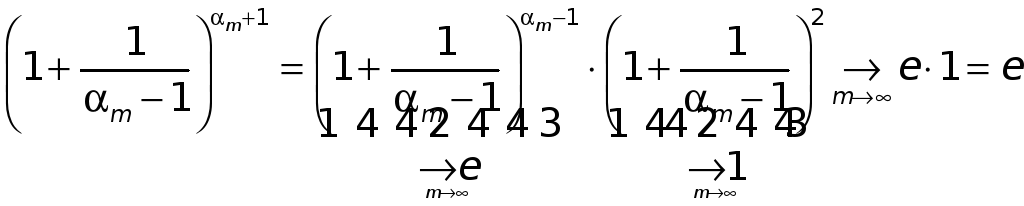 ;
;
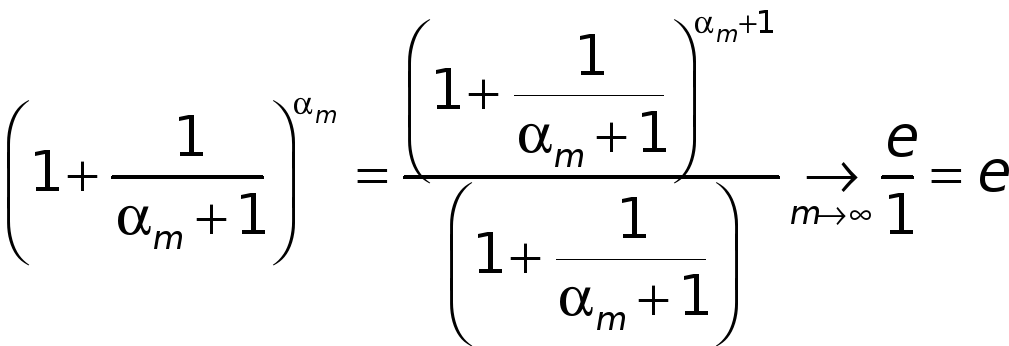 .
.
А тогда из (4), по теореме о сжатой переменной, находим
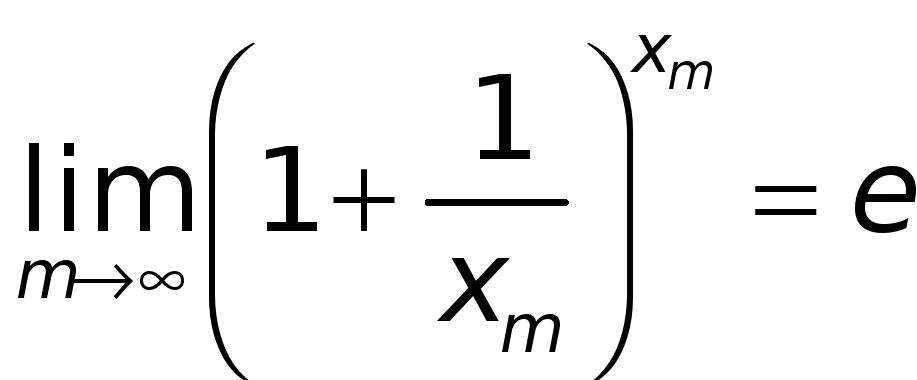 .
.
Подчеркнем еще
раз, что здесь переменная
![]() — любая стремящаяся к
— любая стремящаяся к
![]() .
(
.
(![]() может и не быть монотонной). ◄
может и не быть монотонной). ◄