§ 9. Сравнение бесконечно малых функций

Пусть имеются две функции и , определенные в некоторой окрестности точки , за исключением, быть может, самой точки . Пусть и есть бесконечно малые функции при , т. е. и . Кроме того, предполагаем, что для , где — проколотая окрестность точки (окрестность точки , за исключением самой точки ). Составим отношение .

1. Если 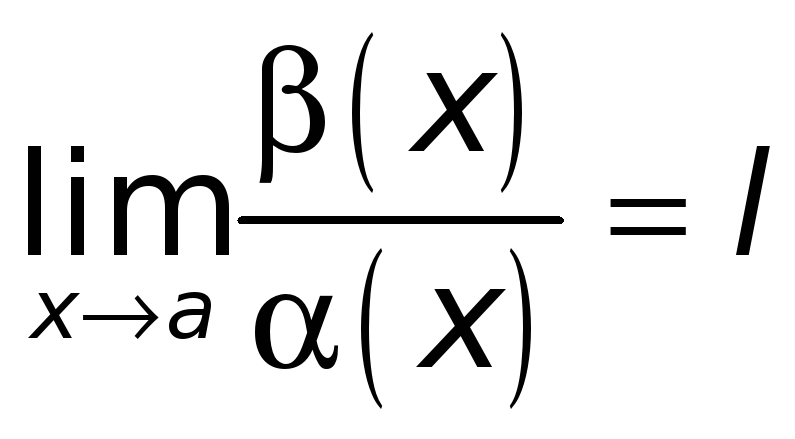, где и , то функции и называют бесконечно малыми одного порядка при .

1а. Если 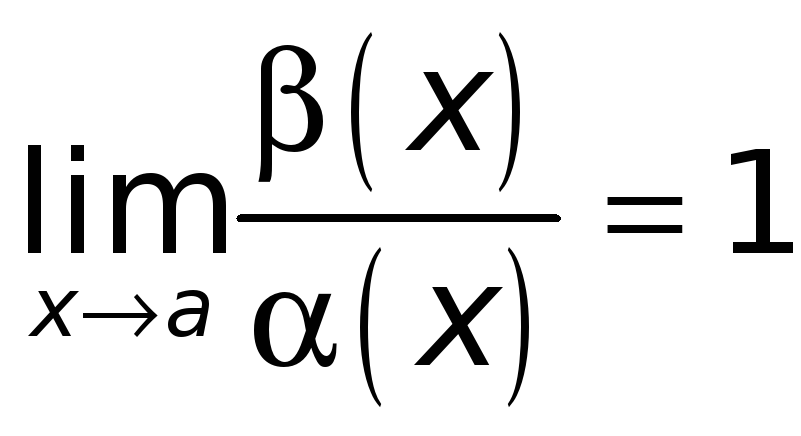, где и , то функции и называют эквивалентными бесконечно малыми при и пишут при .

2. Если 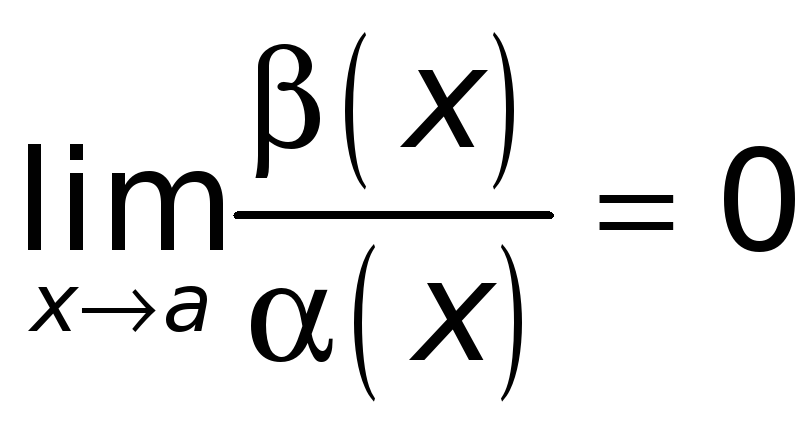, то функцию называют бесконечно малой более высокого порядка по сравнению с при и пишут при . (Читают: « равна о малое от при »).

3. Если 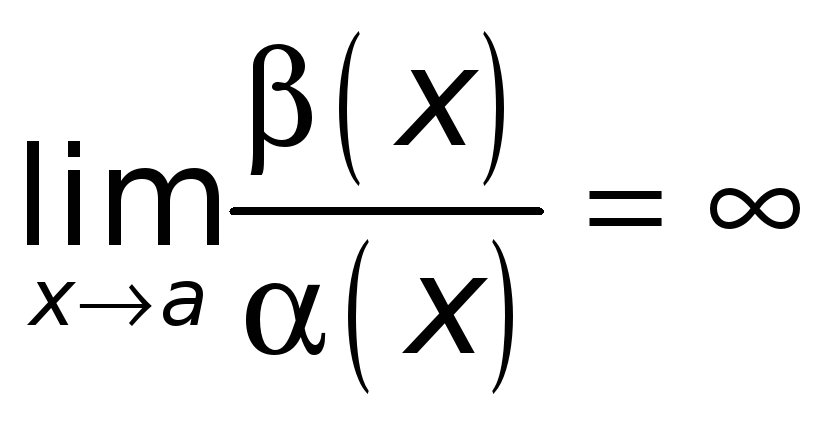, то функцию называют бесконечно малой более низкого порядка по сравнению с при .

4. Если отношение не имеет предела при , то говорят, что бесконечно малые функции и не сравнимы при .

Например, функции и — бесконечно малые при . Имеем . Но не имеет предела при . Значит и не сравнимы при .

5. Пусть и — бесконечно малые функции при и пусть — некоторое число, не обязательно целое. Если 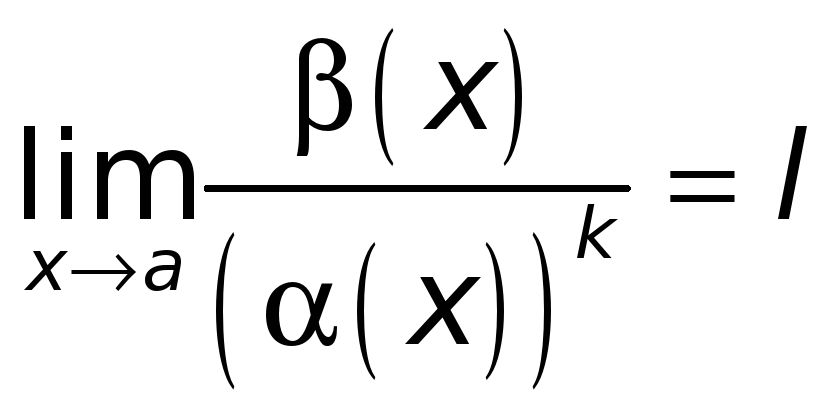где и , то функцию называют бесконечно малой порядка по сравнению с при .

Нетрудно понять, что:

1) если , то функция бесконечно малая одного порядка с при .

2) если , то функция — бесконечно малая более высокого порядка по сравнению с при .

3) если , то функция — бесконечно малая более низкого порядка по сравнению с при .

Теорема 1. Произведение двух бесконечно малых величин является бесконечно малой величиной более высокого порядка по сравнению с каждым из сомножителей.

► Пусть и , и пусть . Требуется показать, что и при . Имеем

.

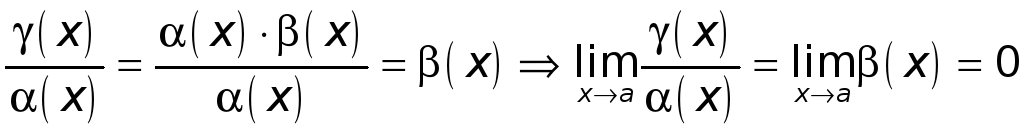А это означает, что при . Имеем, далее,

.

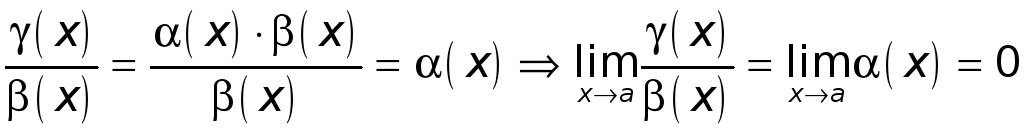Последнее означает, что при . ◄

Теорема 2. Разность двух эквивалентных бесконечно малых величин является бесконечно малой величиной по сравнению с каждой из них.

► Пусть и , и пусть при . Положим . Требуется показать, что и при .

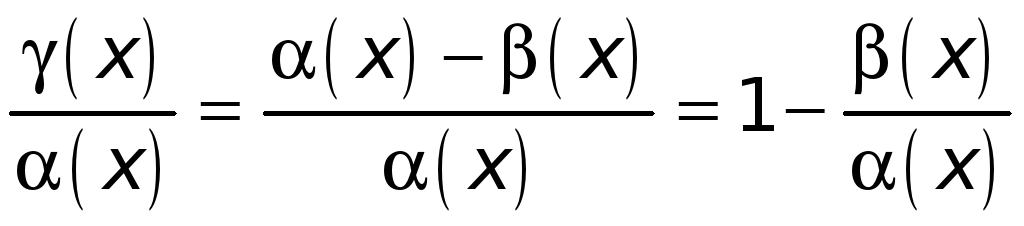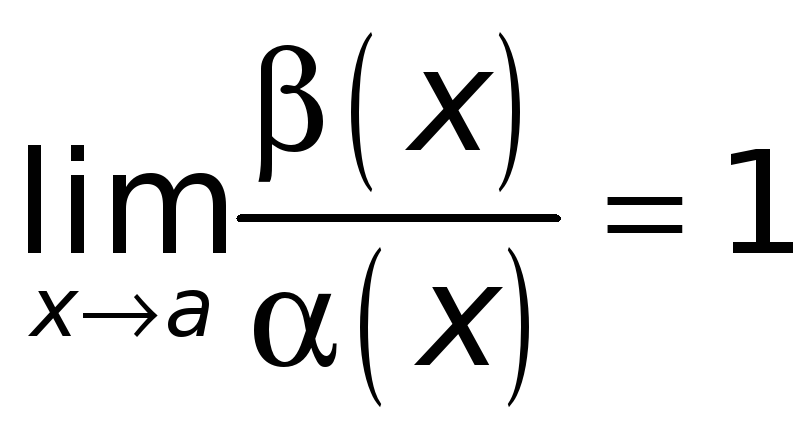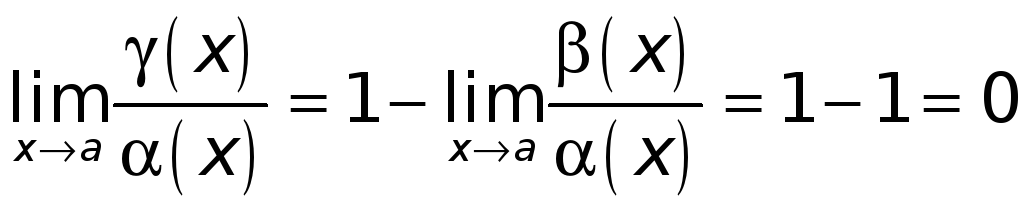Имеем . По условию . Следовательно, . Значит, при .

Имеем, далее, 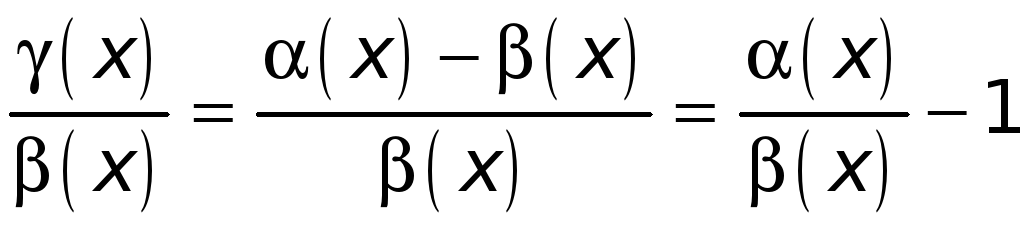. По условию 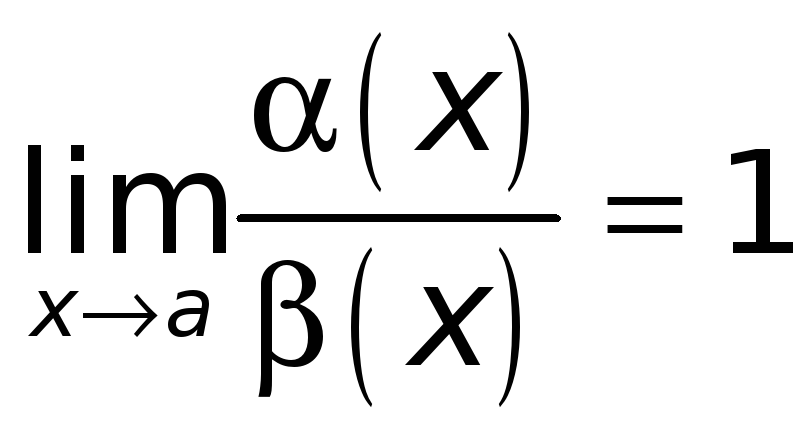. А тогда 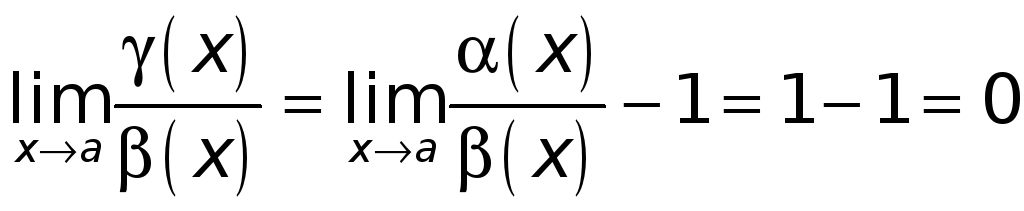. Значит, при . ◄

Теорема 3 (о замене бесконечно малых эквивалентными при отыскании предела отношения). Пусть ,и и пусть , при . Тогда: если существует конечный или бесконечный предел

,

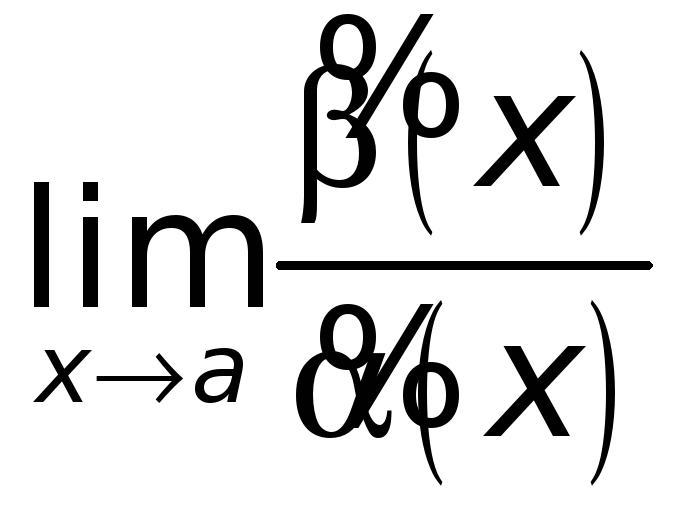то к этому же пределу стремится при и отношение .

► 1) Пусть 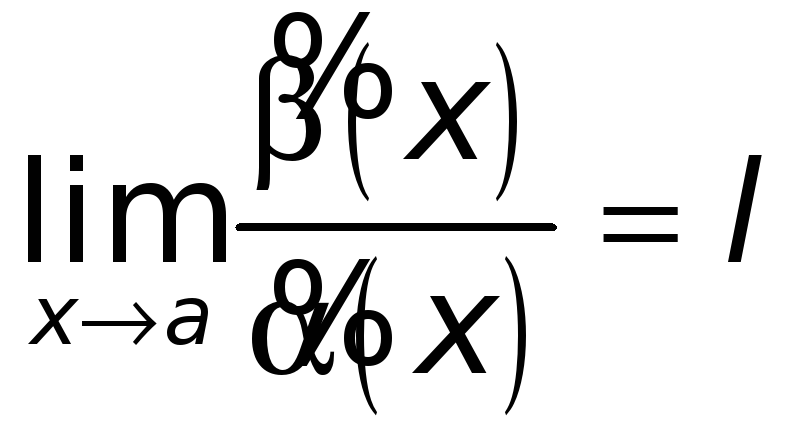, где — конечное число. Напишем очевидное равенство

.

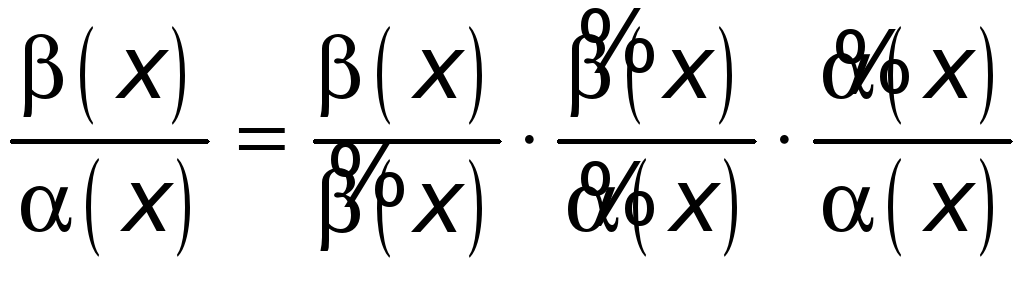По условию каждый из трех сомножителей в правой части имеет конечный предел при . А тогда

,

т.е. .

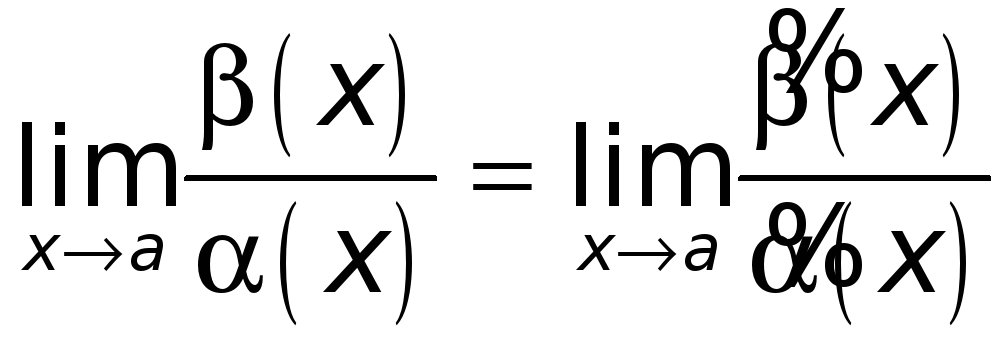2) Пусть теперь 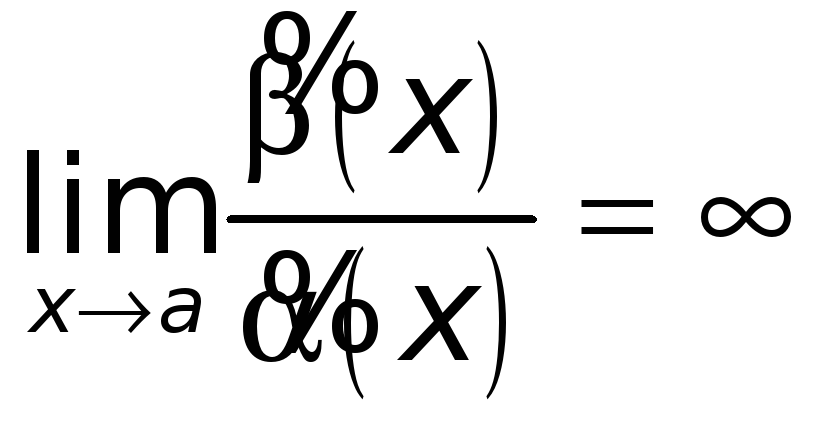. Но тогда 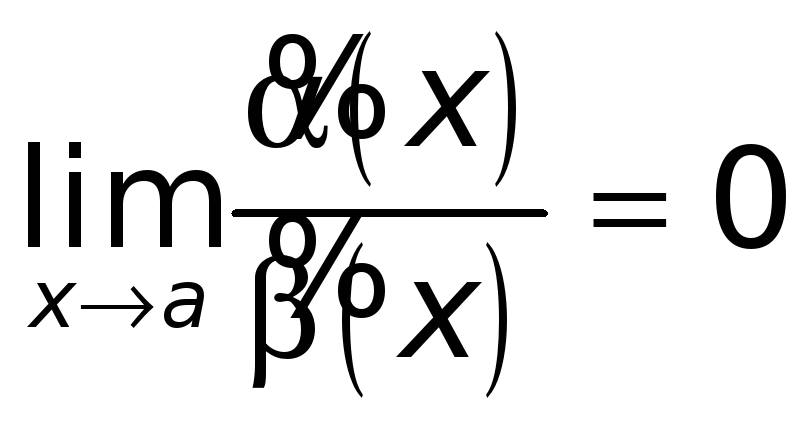(считаем, что для ). Следовательно, по доказанному в пункте 1), 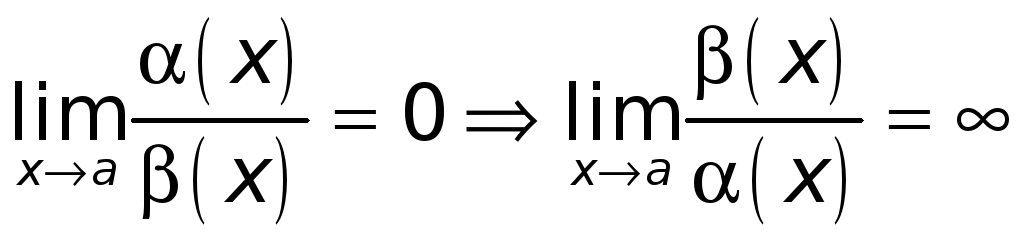. Значит, и в этом случае

.

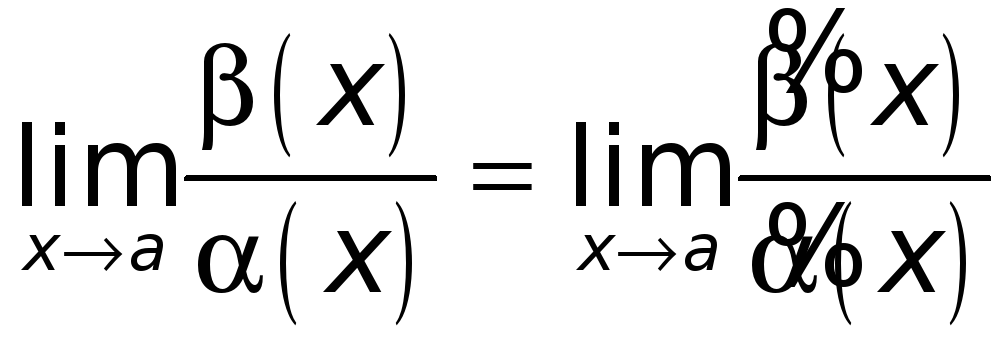Замечание 1. Применение теоремы 3 требует знания бесконечно малых функций и эквивалентных при соответственно бесконечно малым функциям и .

Приведем несколько примеров эквивалентных бесконечно малых функций.

1) при (это так, ибо ).

2) при .

3) при .

4) при ().

5) при .

6) при .

7) при .

8) при .

Соотношения 2) – 8) будут установлены несколько позже.

Замечание 2. Следует остерегаться делать замену бесконечно малых функций на эквивалентные в сумме, ибо если и при , то не всегда при .

Рассмотрим пример. Было отмечено, что при . Значит,

при ,

при .

Однако сумма неэквивалентна сумме при . Действительно, имеем

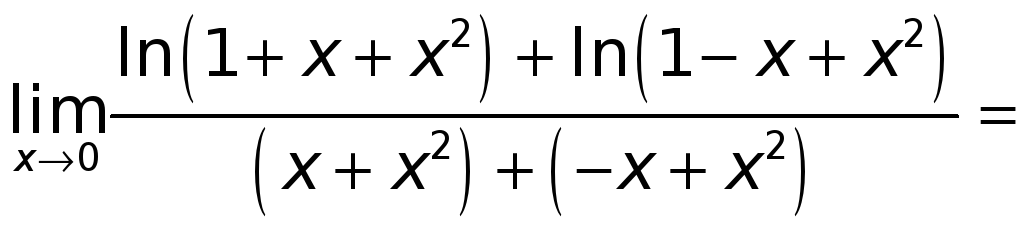
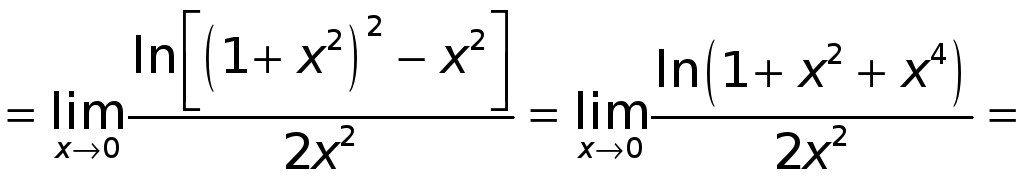
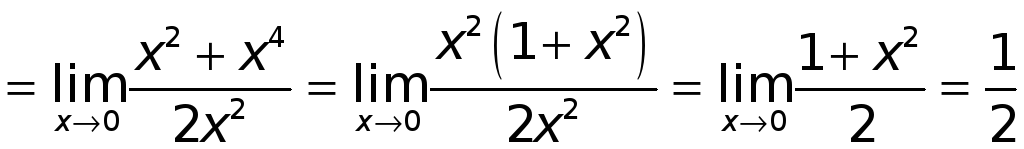(а не 1).