
- •Глава 3 Предельное значение функции. Непрерывность § 1. Предел функции
- •§ 2. Односторонние пределы функции
- •§ 3. Предел отношения синуса к своей дуге
- •§ 4. Число e
- •§ 5. Предел функции при
- •§ 6. Натуральные логарифмы. Показательная функция . Гиперболические функции
- •§ 7. Бесконечно малые и бесконечно большие функции
- •§ 8. Свойства конечных пределов, связанные с арифметическими действиями над функциями
- •§ 9. Сравнение бесконечно малых функций
- •§ 10. Непрерывность функций
- •§ 11. Свойства непрерывных функций
- •2. Арифметические операции над непрерывными функциями.
- •3. Непрерывность сложной функции.
- •§ 12. Непрерывность элементарных функций
- •§ 13. Свойства функций, непрерывных в замкнутом промежутке
- •§ 14. Понятие обратной функции
- •§ 15. Непрерывность элементарных функций (продолжение)
- •§ 16. Три важных предела
- •§ 17. Степенно-показательные выражения
- •§ 18. Теоремы Вейерштрасса
- •§ 19. Понятие равномерной непрерывности функции. Теорема Кантора
- •§ 20. Точки разрыва функций и их классификация
§ 7. Бесконечно малые и бесконечно большие функции
Пусть функция
![]() определена в некоторой окрестности
точки а,
за исключением, быть может, самой точки
а
(в точке а
функция
определена в некоторой окрестности
точки а,
за исключением, быть может, самой точки
а
(в точке а
функция
![]() может быть определена, а может быть и
не определена).
может быть определена, а может быть и
не определена).
Определение.
Функция
![]() называется бесконечно
малой при
называется бесконечно
малой при
![]() ,
если
,
если
![]() .
.
Определение.
Функция
![]() называется бесконечно
большой при
называется бесконечно
большой при
![]() ,
когда либо
,
когда либо
![]() ,
либо
,
либо
![]() ,
либо
,
либо
![]() .
При этом в случае, когда
.
При этом в случае, когда
![]() ,
говорят, что
,
говорят, что
![]() положительная бесконечно большая; а в
случае, когда
положительная бесконечно большая; а в
случае, когда
![]() ,
говорят, что
,
говорят, что
![]() отрицательная бесконечно большая при
отрицательная бесконечно большая при
![]() .
.
Замечание.
Буква а
может обозначать и число, и один из
символов:
![]() ,
,
![]() ,
,
![]() .
.
Определение.
Функция
![]() называется ограниченной при
называется ограниченной при
![]() ,
если существует постоянное число
,
если существует постоянное число
![]() такое, что
такое, что
![]() для всех значений х
в некоторой проколотой окрестности а.
При этом под окрестностью а,
когда а
обозначает один из символов
для всех значений х
в некоторой проколотой окрестности а.
При этом под окрестностью а,
когда а
обозначает один из символов
![]() ,
,
![]() ,
,
![]() ,
соответственно понимают:
,
соответственно понимают:
– в первом случае
— множество всех х,
удовлетворяющих неравенству
![]() , где
, где
![]() — постоянное положительное число;
— постоянное положительное число;
– во втором —
множество всех х,
удовлетворяющих неравенству
![]() ;
;
– в третьем —
множество всех х,
удовлетворяющих неравенству
![]() .
.
На рис. 3.5 приведены
примеры окрестностей
![]() ,
,
![]() ,
,
![]() .
.
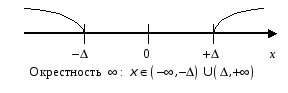
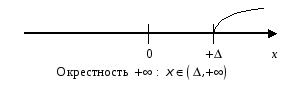
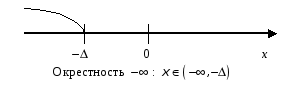
Рис. 3.5. Примеры окрестностей.
Отметим следующие
свойства бесконечно малых и бесконечно
больших функций при
![]() ,
вытекающие из соответствующих свойств
бесконечно малых и бесконечно больших
последовательностей.
,
вытекающие из соответствующих свойств
бесконечно малых и бесконечно больших
последовательностей.
1. Если одна из трех
функций
![]() ,
,
![]() ,
,
![]() является бесконечно малой при
является бесконечно малой при
![]() ,
то и две другие функции также являются
бесконечно малыми при
,
то и две другие функции также являются
бесконечно малыми при
![]() .
.
2. Если одна из трех
функций
![]() ,
,
![]() ,
,
![]() является бесконечно большой при
является бесконечно большой при
![]() ,
то и две другие функции также являются
бесконечно большими при
,
то и две другие функции также являются
бесконечно большими при
![]() .
.
3. Если функция
![]() — бесконечно малая при
— бесконечно малая при
![]() ,
а функция
,
а функция
![]() — ограниченная при
— ограниченная при
![]() то произведение
то произведение
![]() есть бесконечно малая функция при
есть бесконечно малая функция при
![]() .
.
4. Если функция
![]() — бесконечно большая при
— бесконечно большая при
![]() ,
а функция
,
а функция
![]() имеет отличный от нуля предел при
имеет отличный от нуля предел при
![]() ,
то произведение
,
то произведение
![]() есть бесконечно большая функция при
есть бесконечно большая функция при
![]() .
.
5. Если функция
![]() — бесконечно малая при
— бесконечно малая при
![]() и
и
![]() в некоторой проколотой окрестности
точки
в некоторой проколотой окрестности
точки
![]() ,
то
,
то
![]() есть функция бесконечно большая при
есть функция бесконечно большая при
![]() .
.
6. Если функция
![]() — бесконечно большая при
— бесконечно большая при
![]() ,
то
,
то
![]() есть функция бесконечно малая при
есть функция бесконечно малая при
![]() .
.
Остановимся для примера на доказательстве одного из этих свойств, например, свойства 4 (все другие свойства доказываются совершенно аналогично).
Дано: 1)
![]() — бесконечно большая функция при
— бесконечно большая функция при
![]() ,
т. е.
,
т. е.
![]() ;
;
![]() .
.
Требуется доказать,
что
![]() — бесконечно большая функция при
— бесконечно большая функция при
![]() .
.
► Составляем
последовательность
![]() значений
значений
![]() ,
любую, но такую, что
,
любую, но такую, что
![]() (предполагается, что
(предполагается, что
![]() берутся из окрестности точки
берутся из окрестности точки
![]() и
и
![]() ).
).
По условию
![]() .
Но тогда и
.
Но тогда и
![]() .
По условию
.
По условию
![]() — бесконечно большая функция при
— бесконечно большая функция при
![]() .
Но тогда и
.
Но тогда и
![]() — бесконечно большая последовательность
при
— бесконечно большая последовательность
при
![]() .
Следовательно,
.
Следовательно,
![]() — бесконечно большая последовательность,
как произведение бесконечно большой
последовательности и последовательности,
имеющей конечный предел, отличный от
нуля.
— бесконечно большая последовательность,
как произведение бесконечно большой
последовательности и последовательности,
имеющей конечный предел, отличный от
нуля.
Так как
последовательность
![]() — любая, сходящаяся к точке
— любая, сходящаяся к точке
![]() ,
то заключаем, что
,
то заключаем, что
![]() .
А это означает, что функция
.
А это означает, что функция
![]() — бесконечно большая при
— бесконечно большая при
![]() .
◄
.
◄
§ 8. Свойства конечных пределов, связанные с арифметическими действиями над функциями
Сразу отметим, что
свойства конечных пределов, связанные
с арифметическими действиями над
переменными, пробегающими последовательности
значений, полностью переносятся на
случай, когда конечные пределы при
![]() имеют функции. При этом предполагается,
что все рассматриваемые ниже функции
определены в некоторой окрестности
точки а,
за исключением, быть может, самой точки
а.
имеют функции. При этом предполагается,
что все рассматриваемые ниже функции
определены в некоторой окрестности
точки а,
за исключением, быть может, самой точки
а.
Упомянутую
окрестность точки а будем обозначать
через
![]() .
А тогда
.
А тогда
![]() — проколотая окрестность точки а.
— проколотая окрестность точки а.
1. Если функция
![]() при
при
![]() имеет конечный предел А,
то разность
имеет конечный предел А,
то разность
![]() есть бесконечно малая функция при
есть бесконечно малая функция при
![]() .
.
► Возьмем
последовательность
![]() значений
значений
![]() любую, но такую, что
любую, но такую, что
![]() и
и
![]() .
.
По условию
![]() .
Но тогда
.
Но тогда
![]() .
.
Так как
последовательность
![]() — любая, сходящаяся к точке
— любая, сходящаяся к точке
![]() ,
то заключаем, что
,
то заключаем, что
![]() .
А последнее означает, что разность
.
А последнее означает, что разность
![]() есть бесконечно малая функция при
есть бесконечно малая функция при
![]() .
◄
.
◄
2. Если разность
между функцией
![]() и некотором постоянным числом А
при
и некотором постоянным числом А
при
![]() есть бесконечно малая функция, то число
А
есть предел функции
есть бесконечно малая функция, то число
А
есть предел функции
![]() при
при
![]() .
.
► Возьмем
последовательность
![]() значений х
любую, но такую, что
значений х
любую, но такую, что
![]() и
и
![]() .
.
По условию
![]() есть бесконечно малая функция при
есть бесконечно малая функция при
![]() ,
т. е.
,
т. е.
![]() .
Но тогда
.
Но тогда
![]() .
.
Так как
последовательность
![]() ,
сходящаяся к точке а,
то заключаем, что
,
сходящаяся к точке а,
то заключаем, что
![]() .
◄
.
◄
3. Пусть имеются
две функции
![]() и
и
![]() ,
определенные в
,
определенные в
![]() всюду, за исключением, быть может, точки
а.
Пусть
всюду, за исключением, быть может, точки
а.
Пусть
![]() ,
,
![]() ,
где А
и В
— конечные числа. Тогда функции
,
где А
и В
— конечные числа. Тогда функции
![]() также имеют конечный предел при
также имеют конечный предел при
![]() ,
причем
,
причем
![]() .
.
► Возьмем
последовательность
![]() значений х
любую, но такую, что
значений х
любую, но такую, что
![]() и
и
![]() .
.
По условию
![]() ,
,
![]() .
Но тогда
.
Но тогда
![]() ;
;
![]() .
Следовательно,
.
Следовательно,
![]() (для последовательностей это свойство
нам известно).
(для последовательностей это свойство
нам известно).
Так как
последовательность
![]() любая, сходящаяся к точке а,
то заключаем, что
любая, сходящаяся к точке а,
то заключаем, что
![]() .
◄
.
◄
Заметим, что доказанное свойство распространяется на любое конечное число слагаемых.
4. Пусть имеются
две функции
![]() и
и
![]() ,
определенные в
,
определенные в
![]() всюду, за исключением, быть может, точки
а.
Пусть
всюду, за исключением, быть может, точки
а.
Пусть
![]() ,
,
![]() ,
где А
и В
— конечные числа. Тогда функция
,
где А
и В
— конечные числа. Тогда функция
![]() также имеет конечный предел при
также имеет конечный предел при
![]() ,
причем
,
причем
![]() .
.
► Возьмем
последовательность
![]() значений х
любую, но такую, что
значений х
любую, но такую, что
![]() и
и
![]() .
.
По условию
![]() ,
,
![]() .
Но тогда
.
Но тогда
![]() ,
,
![]() .
Но для последовательностей, как мы
знаем, имеет место свойство
.
Но для последовательностей, как мы
знаем, имеет место свойство
![]() .
У нас последовательность
.
У нас последовательность
![]() любая, сходящаяся к точке а.
Следовательно,
любая, сходящаяся к точке а.
Следовательно,
![]() .
◄
.
◄
Заметим, что доказанное свойство распространяется на любое конечное число сомножителей.
5. Пусть имеются
две функции ф(х) и у(х), определенные в
![]() всюду, за исключением, быть может, точки
а.
Пусть
всюду, за исключением, быть может, точки
а.
Пусть
![]() ;
;
![]() ,
,
![]() и
и
![]() ,
где
,
где
![]() и
и
![]() — конечные числа и
— конечные числа и![]() .
Тогда функция
.
Тогда функция
![]() также имеет конечный предел при
также имеет конечный предел при
![]() ,
причем
,
причем
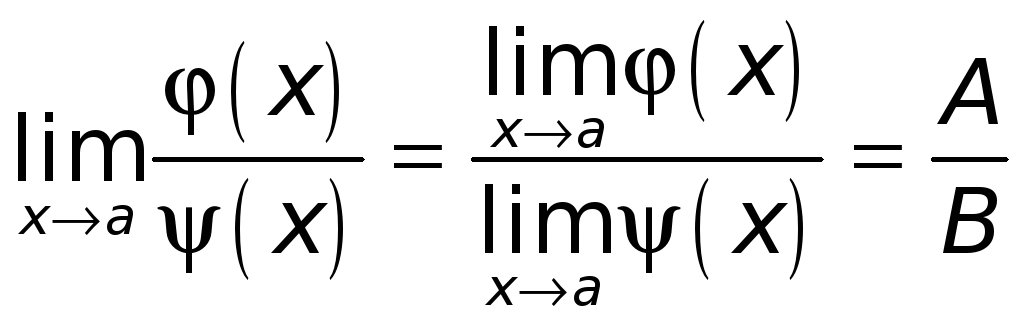 .
.
► Возьмем
последовательность
![]() значений х
любую, но такую, что
значений х
любую, но такую, что
![]() и
и
![]() .
.
Имеем, по условию
![]() =>
=>
![]() .
Имеем, далее,
.
Имеем, далее,
![]() =>
=>
![]() ,
причем
,
причем
![]() и при всех
и при всех
![]() :
:
![]() .
Но для таких последовательностей, как
мы знаем, справедливо соотношение
.
Но для таких последовательностей, как
мы знаем, справедливо соотношение
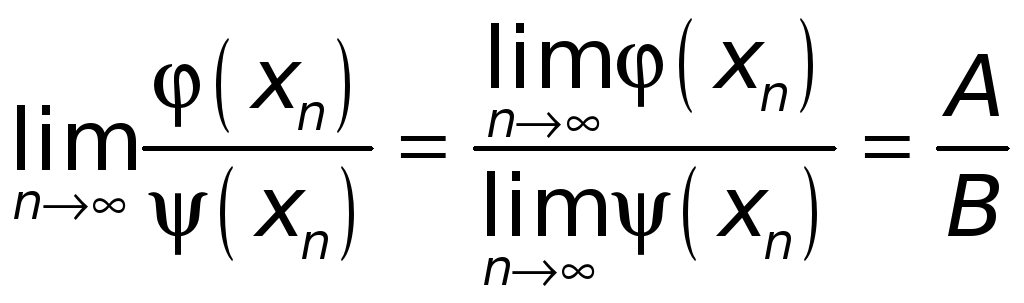 .
.
Так как
последовательность
![]() любая, сходящаяся к точке а,
то, в соответствии с определением предела
функции "на языке последовательностей",
заключаем, что
любая, сходящаяся к точке а,
то, в соответствии с определением предела
функции "на языке последовательностей",
заключаем, что
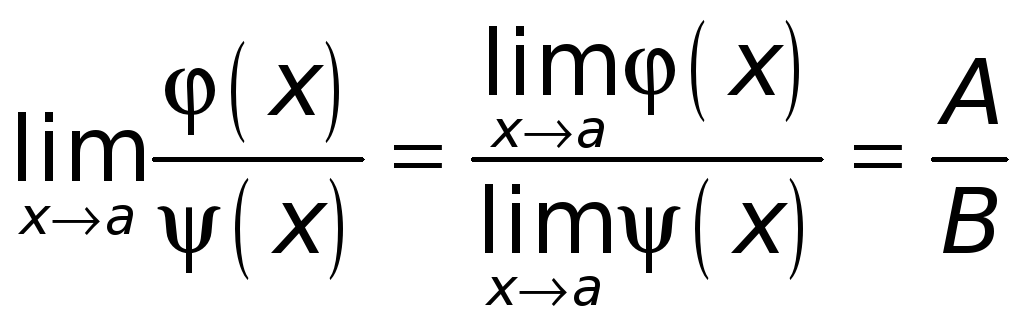 .
◄
.
◄
