
- •Случайные события
- •Стохастический мир
- •Случайные величины
- •Совместная и условная вероятности
- •Зависимость и независимость
- •Характеристическая функция
- •Модель аддитивного блуждания
- •Случайные процессы
- •Стохастические уравнения
- •Уравнение Ито
- •Остановка перед восхождением
- •Лемма Ито
- •Точные решения
- •Простые стохастические модели
- •Представление решений
- •Автокорреляция и спектр
- •Порождающий процесс Винера
- •Средние значения
- •Динамическое уравнение для средних
- •Процесс Феллера
- •Логистическое уравнение
- •Вероятности
- •Марковские плотности вероятности
- •Граничные условия
- •Стохастические интегралы
- •Площадь под траекторией Винера
- •Интегралы Ито
- •Интегрирование стохастических уравнений
- •Единственность решений
- •Метод последовательных приближений
- •Системы уравнений
- •Скоррелированные блуждания
- •Системы стохастических уравнений
- •Стохастический осциллятор
- •Линейные многомерные модели
- •Многомерие помогает одномерию
- •Как решать стохастические задачи?
- •Стохастическая природа
- •Теория броуновского движения
- •Стохастический осциллятор
- •Дрожание земной оси
- •Электронный шум
- •Хищники и их жертвы
- •Стохастическое общество
- •Финансовые рынки
- •Эмпирические закономерности
- •Диверсификация
- •Портфель на всю жизнь
- •Опционы
- •Кривая доходности
- •Компьютерное моделирование
- •Статистики
- •Случайные числа
- •Моделирование стохастических процессов
- •Ошибки вычислений и ускорение сходимости
- •Вычисление средних
- •R: Стохастический справочник
- •Основные соотношения теории
- •Системы уравнений с одинаковым шумом
- •M: Математические приложения
- •H: Помощь
- •C: Примечания
- •Рекомендуемая литература
34 |
Глава 1. |
1.7Модель аддитивного блуждания
Координата броуновской частицы в воде или цена на финансовом рынке x имеют траекторию с очень нерегулярными изломами. Простей-
шим е¼ описанием будет модель аддитивного независимого дискретного случайного блуждания. Все четыре прилагательных в названии модели отражают базовые свойства процесса.
Предположим, что начальное значение x = x0. Далее x испытывает t = 1; 2; ::: случайных независимых гауссовых изменений ( толчков ), каждое с волатильностью . В результате x окажется равным накопленной сумме таких изменений:
xt = x0 + ("1 + ::: + "t); |
(1.38) |
ãäå "i N(0; 1) гауссовы числа с нулевым средним и единичной дисперсией. Индекс t пока является целым числом, однако в дальнейшем мы перейд¼м к пределу непрерывного времени.
Удобно ввести дискретную переменную Винера: |
|
||||
Wt = "1 + ::: + "t = " p |
|
|
|
||
t: |
(1.39) |
||||
Второе равенство мы записали, так как сумма |
|
t гауссовых чисел снова |
|||
равна гауссовому числу с волатильностью p |
|
|
|
||
t |
(ñòð. 22 23). Случайные |
||||
числа, как с индексами "i, так и без них ", предполагаются нормированными: h"i = 0, "2 = 1, т.е. как " N(0; 1). Модель (1.38) теперь
выглядит следующим образом: xt = x0 + Wt.
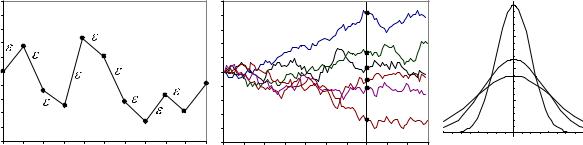
Начиная с x0 = 0, будем генерить случайные числа "1, "2, ... è ñòðî- ить их накопленную сумму. Такая траектория называется выборочной траекторией случайного процесса (1-й рисунок):
xt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
4 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
9 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
xt |
0 |
t |
0.4 |
|
P(x,t) |
t=1 |
|
|
|
t=3 |
|
t=5 |
|
x |
|
0 |
Так как изменения "k будут каждый раз новыми, то по-разному будут протекать и блуждания траектории xt = x(t) (см. 2-й рисунок). Различ- ные реализации процесса блуждания пересекают вертикальную прямую t = const в тех или иных значениях x. Совокупность всех этих чисел является случайной величиной.

Случайные события |
35 |
Поэтому, говоря о процессе x(t), мы подразумеваем, что в данный момент времени x = x(t) имеет определ¼нное распределение P (x). В неко-
торый другой момент времени распределение может оказаться иным. Поэтому плотность вероятности P (x; t), среднее x(t) и волатильность (t)
будут функциями времени. |
p |
|
|
Волатильность аддитивного блуждания увеличивается, как |
|
|
|
. Ýòî |
|||
|
t |
||
наглядно видно на 2-м рисунке с несколькими реализациями xt. Èõ ïó- чок постепенно расширяется. В результате неопредел¼нность будущего значения xt увеличивается. Мы можем обнаружить xt достаточно дале- ко от начального значения x0 = 0. Это также проиллюстрировано на 3-м рисунке, где представлены плотности вероятности P (x; t), которые с течением времени постепенно расплываются .
Блуждающие траектории начинаются с определ¼нного начального зна- чения x0 = x(t0) в момент времени t0. Поэтому, говоря о вероятности, мы имеем дело с условной плотностью P (x0; t0 ) x; t). Пока моменты времени t0 и t являются целыми числами, соответствующими номеру скачка "k на очередном этапе.
Важно понимать, что xt = x(t) не является конкретной траекторией. Это одновременная совокупность всех возможных траекторий случайного процесса. Аналогично, случайное число x не подразумевает конкрет-
ного значения, а обозначает все возможные реализации, подчиняющиеся некоторому распределению P (x). Вероятность получить на t-ом шаге xt определяется вероятностями всех изменений "i. Так, дискретный вине- ровский процесс Wt определяется плотностью вероятности:
P ("1; :::; "t) = P ("1) ::: P ("t);
где равенство отражает независимость всех "i. Таким образом, Wt ôàê-
тически, многомерная случайная величина. p Обратим ещ¼ раз внимание на смысл записи: "1 + ::: + "t = " t.
Предположим, что в процессе моделирования мы генерим t независимых гауссовых чисел "1; "2; ::: и складываем их. Результат будет иметь такие
же статистические свойства, как одно гауссово число " с единичной |
||
p |
|
|
. При вычислении свойств |
||
волатильностью, умноженное на фактор |
t |
|
накопленной суммы вполне достаточно пользоваться величиной ", а не
совместной плотностью P ("1; :::; "t). В частности, если мы ищем среднее значение, в котором участвует сумма гауссовых чисел, его вычисление можно упростить, используя только одно случайное число. Однако, если нас интересует связь сумм, получаемых в различные моменты времени, то необходимы некоторые ухищрения. Рассмотрим их подробнее.
36 |
Глава 1. |
Для сравнения процесса блуждания с самим собой в различные мо-
менты времени его необходимо разбивать на неперекрывающиеся участки времени. Пусть процесс длится s шагов, а затем еще в течение t s.
Сравним свойства траекторий в моменты времени s и t (s < t):
Ws = "1 + ::: + "s;
Wt = "1 + ::: + "s + "s+1 + ::: + "t:
Вычитая уравнения, получим сумму t s случайных чисел:
p
Wt Ws = "s+1 + ::: + "t = " t s = Wt s:
Второе равенство является отражением того, что суммарная âîëàòèëü- |
||||||||||||
ность |
t s |
независимых гауссовых слагаемых будет равна |
p |
t s |
. Ôàê- |
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
тически, Ws è Wt можно представить в виде: |
|
|
|
|||||||||
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
Ws = "a p |
s; |
p |
|
|
|
|
(1.40) |
|||
|
|
|
|
|
|
|
||||||
|
|
Wt = "a s + "b |
t s; |
|
|
|
||||||
ãäå "a, "b, как и везде в наших лекциях, независимые гауссовые числа с нулевым средним и единичной дисперсией. Первое из них "a ýêâè- валентно накопленной сумме начальных s приращений, а второе "b соответствует независимым от "a последующим t s приращениям.
Теперь можно найти ковариацию между Ws è Wt. Òàê êàê Wt = 0, òî:
|
|
|
|
p |
|
|
|
p |
|
|
p |
|
|
|
|
â ñèëó òîãî, ÷òî |
|
|
|
|
|
|
|
|
|
|
|||||
cov(s; t) = hWsWti = |
"a |
|
|
s |
"a |
|
s + "b |
|
t s = s; |
||||||
зависит только от |
|
|
|
|
|
|
s |
= min(s; t) |
|
|
|||||
|
"2 |
= 1 è |
" |
" |
bi |
= 0. Таким образом, ковариация |
|||||||||
|
a |
|
h a |
|
|
|
|
|
|
|
|
|
|
||
|
наименьшего числа |
|
|
|
|
|
|
, представляющего |
|||||||
собой длительность общей для Ws è Wt истории. Для прояснения смысла
этого результата запишем регрессионную прямую (1.25) между W |
s |
è W |
t. |
||||||||||||||||
Их волатильности равны p |
|
|
è p |
|
|
, а средние нулю, поэтому: |
|
||||||||||||
|
|
t |
|
|
|||||||||||||||
s |
|
|
|
||||||||||||||||
Wt |
cov(s; t) Ws |
|
|
|
|
|
|||||||||||||
p |
|
= |
p |
|
p |
|
p |
|
|
+ p |
|
|
=> Wt = Ws + : |
|
|
|
|||
t |
t |
s |
t |
|
|
|
|||||||||||||
s |
|
|
|
||||||||||||||||
Таким образом, если известно, что в момент времени s сумма равна Ws, то наилучшим прогнозом будущего значения Wt будет уже известное Ws. Èç (1.40) следует, что линейная регрессионная модель оказывается в дан-
ном случае точной (l C9). При этом е¼ шумом выступают накопленныеp после момента времени s изменения: = "s+1 + ::: + "t = "b t s.
Мы будем часто усреднять гауссовы величины, поэтому в качестве упражнения стоит проверить следующие соотношения ( i < j < k):
hWiWjWki = 0; |
Wi2WjWk = 2i2 + ij; |
WiWj2Wk = 3ij: |
[Процесс Wk необходимо разбить на три интервала ( l C10).]

Случайные события |
37 |
В заключение раздела ответим на следующий вопрос. Если x = x1 â момент времени t = t1, то какова вероятность обнаружить его на следу- þùåì øàãå t = t2 в значении x2? Очевидно, что она равна вероятности изменения x:
P (x1 |
|
x2) = e |
|
|
|
= exp |
2(t2 t1) |
: |
|||
|
|
|
|
"2 |
=2 |
|
|
(x2 x1)2 |
|
|
|
|
) |
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2 |
|
|
|
|
|
||||
Мы положили = 1 и записали в явномp |
2 (t2 t1) |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||
виде гауссову плотность веро- ятности для " = x2 x1. В результате условная вероятность зависит от обоих аргументов, поэтому случайные числа x1 è x2 являются зависимы- ìè.
Дискретная траектория блуждания описывается множеством случайных величин xt = fx1; x2; x3; :::g, задающих возможные значения x на ша-
ге t. Индекс можно записать в функциональной форме x(t) и говорить о
случайной функции, которая пока определена только в дискретных точ- ках. Таким образом, случайная функция это многомерная величина. Для задания свойств случайного процесса в общем случае необходимо определить плотность вероятности P (x1; x2; x3; :::) с бесконечным числом аргументов.
Для винеровского процесса ситуация существенно упрощается, так как каждое следующее xt+1
шествующего xt и никак не зависит от более длинной предыстории. Этот факт мы будем записывать в следующем виде ( l C11):
P (x1; :::; xt ) xt+1) = P (xt ) xt+1): |
(1.41) |
Если известно xt, òî xt+1 будет определяться значением xt и случайным изменением ", а не всей историей x1; :::; xt 1. Процессы с такой корот- кой памятью называются марковскими процессами. Они представляют собой следующее приближение после независимости случайных величин, для которых P (x1; :::; xt ) xt+1) = P (xt+1):
Марковские процессы позволяют представить совместную вероятность любой размерности в виде цепочки условных вероятностей. Например:
P (x1; x2; x3) = P (x1) P (x1 ) x2) P (x2 ) x3): |
(1.42) |
Для этого сначала записываем P (x1; x2; x3) = P (x1; x2) P (x1; x2 ) x3) по определению условной вероятности. Затем используем определение для P (x1; x2) = P (x1)P (x1 ) x2) и марковское условие короткой памяти: P (x1; x2 ) x3) = P (x2 ) x3). Таким образом, чтобы произошло x1; x2; x3, необходимо, чтобы свершилось x1. При условии, что это про- изошло, далее реализовалось x2, è ò.ä.
