
- •Случайные события
- •Стохастический мир
- •Случайные величины
- •Совместная и условная вероятности
- •Зависимость и независимость
- •Характеристическая функция
- •Модель аддитивного блуждания
- •Случайные процессы
- •Стохастические уравнения
- •Уравнение Ито
- •Остановка перед восхождением
- •Лемма Ито
- •Точные решения
- •Простые стохастические модели
- •Представление решений
- •Автокорреляция и спектр
- •Порождающий процесс Винера
- •Средние значения
- •Динамическое уравнение для средних
- •Процесс Феллера
- •Логистическое уравнение
- •Вероятности
- •Марковские плотности вероятности
- •Граничные условия
- •Стохастические интегралы
- •Площадь под траекторией Винера
- •Интегралы Ито
- •Интегрирование стохастических уравнений
- •Единственность решений
- •Метод последовательных приближений
- •Системы уравнений
- •Скоррелированные блуждания
- •Системы стохастических уравнений
- •Стохастический осциллятор
- •Линейные многомерные модели
- •Многомерие помогает одномерию
- •Как решать стохастические задачи?
- •Стохастическая природа
- •Теория броуновского движения
- •Стохастический осциллятор
- •Дрожание земной оси
- •Электронный шум
- •Хищники и их жертвы
- •Стохастическое общество
- •Финансовые рынки
- •Эмпирические закономерности
- •Диверсификация
- •Портфель на всю жизнь
- •Опционы
- •Кривая доходности
- •Компьютерное моделирование
- •Статистики
- •Случайные числа
- •Моделирование стохастических процессов
- •Ошибки вычислений и ускорение сходимости
- •Вычисление средних
- •R: Стохастический справочник
- •Основные соотношения теории
- •Системы уравнений с одинаковым шумом
- •M: Математические приложения
- •H: Помощь
- •C: Примечания
- •Рекомендуемая литература

88 |
Глава 3. |
3.3Логистическое уравнение
Динамика роста в условиях ограниченности ресурсов описывается
при помощи логистического уравнения (стр. 10). Рассмотрим его стохастический аналог с начальным условием x0 = x(0):
dx = ( x x2) dt + x W:
Прежде чем приступить к анализу задачи, стоит уменьшить число параметров, проведя скейлинговые замены: t ! t= , x ! x = . В этих
переменных уравнение принимает вид:
p
dx = x (1 x) dt + 2 x W;
ãäå = 2=2 . При масштабировании времени мы воспользовались тем, p
что W = " dt. Таким образом, с точностью до размерных преобразований свойства решения определяются единственным параметром . Найдя решение уравнения, мы всегда можем сделать обратное преобразование:
t ! t; x ! |
|
x0 ! |
|
||
|
x; |
|
x0: |
||
|
|
||||
В детерминированном случае ( = 0) задача имеет простое решение:
dx |
= a(x) = x (1 x) |
=> |
x(t) = |
1 |
; |
|
|
||||
dt |
1 (1 1=x0) e t |
В пределе t ! 1, при любом начальном условии x0, решение стремится к равновесному значению x = 1. Если в этой точке оно находится с самого начала x0 = 1, то решение там и оста¼тся и не зависит от времени.
Качественно это поведение легко понять. Уравнение a(x1) = 0 имеет две особые точки x1 = 0 è x1 = 1. Если разложить a(x) в окрестности особой точки в ряд по отклонениям от не¼, то уравнение примет вид:
dxdt = a(x) a0(x1) (x x1) + ::
Åñëè a0(x1) > 0, то это точка неустойчивого равновесия. Действительно, при x > x1 производная dx=dt будет положительна, и x начн¼т увеличи-
ваться, удаляясь от x1. Устойчивое равновесие возможно только, если a0(x1) < 0. Поэтому для логистического уравнения единственной устой-
чивой точкой является x1 = 1. Именно к ней, в пределе больших врем¼н, и стремится решение.

Средние значения |
89 |
В стохастическом случае решение найти не так просто. Для анализа асимптотических свойств при t ! 1 воспользуемся динамическим уравнением для средних (3.3), ñòð. 78, ñ F = ln x è F = x:
hln_xi = 1 hxi hx_ i = hxi x2 :
Положив производные по времени равными нулю, получаем:
hxi = 1 ; |
x2 = hxi ; x2 = (1 ) : |
(3.13) |
Как мы видим, стохастичный шум уменьшает численность популяции, которая в детерминированном случае стремится к 1. Обратим внимание
на то, что положительная дисперсия возможна только при < 1. Стационарное уравнение Фоккера-Планка приводит к гамма-распределению:
P (x) = 1 x 1 e x= ;( )
где = (1 )= . В окрестности максимума xmax = ( 1)= гамма - распределение можно приближ¼нно описать гауссианой. Если велико, то
максимум сдвигается впраâо, и его относительная ширина уменьшается. Асимметрия asym = 2=p и эксцесс excess = 6= распределения стре-
мятся к нулю при ! 1. Плотность P (x) несимметрична (см. стр. 83),
поэтому характеристикой значений случайной величины может служить как hxi, так и xmax.
Выберем теперь в динамическом уравнении F = 1=x:
hx_ 1i = (2 1) |
x 1 + 1; |
(3.14) |
откуда:
x 1 = |
1 |
+ |
1 |
|
e(2 1) t |
1 |
: |
(3.15) |
|
|
|
|
|
|
|||||
x0 |
2 1 |
2 1 |
|||||||
Обратная функция нелинейна (1=x 6= 1=x), и это решение не да¼т нам возможности найти x(t). Заметим, что y(t) = 1=x(t), в силу леммы Ито, удовлетворяет линейному уравнению:
p
dy = 1 + (2 1)y dt 2 y W:
Несмотря на особенность в знаменателе (3.15), при = 1=2 решение не
обращается в бесконечность. В этом легко убедиться, разложив экспоненту в ряд при малых 2 1. В результате предел решения при ! 1=2 имеет вид: x 1 = x0 1 + t: Этот результат можно получить сразу из исходного уравнения (3.14), положив = 1=2.
90 |
Глава 3. |
Поведение решения можно исследовать численными методами. Для
этого, при помощи итерационной процедуры (стр. 49), генерится большое количество выборочных траекторий. По ним находят среднее hxi,
волатильности x(t) или плотность вероятности P (x0; t0 ) x; t). Детали реализации подобных вычислений на языке C++ мы рассмотрим в
девятой главе, а сейчас привед¼м графики поведения среднего и волатильности процесса.
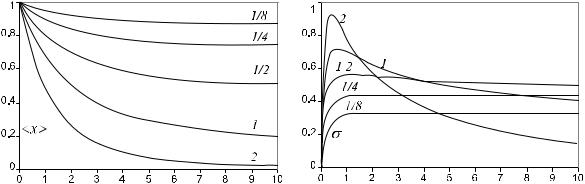
В качестве начального условия выберем x0 = 1. Слева на рисунках представлены средние значения при различных параметрах (числа возле линий), а справа волатильности:
Если < 1, то среднее значение стремится к не нулевому уровню hxi = 1 . При > 1 и среднее, и волатильность стремятся к нулю. Это
означает, что при большом стохастическом шуме решение вырождается в константу x = 0. Этот результат качественно отличается от детерми-
нированной задачи, где решение всегда стремилось к x = 1. Причина
подобного поведения состоит в следующем. Снос уравнения имеет точ- ку устойчивого равновесия x = 1. Она не да¼т процессу при блуждании
уходить далеко вверх. В результате происходят колебания вокруг равновесного уровня, в процессе которых, рано или поздно, процесс оказывается в значении x = 0. В этот момент снос и волатильность в уравнении
обращаются в ноль, и, несмотря на наличие стохастического члена, дальнейшее изменение x прекращается, так как dx = 0.
Значение x = 0 является точкой неустойчивого равновесия, и малей-
шее внешнее возмущение может решение с не¼ столкнуть, в том числе и в область x < 0. Поэтому, вообще говоря, логистическое уравнение
необходимо дополнить граничным условием в x = 0.
Если в качестве начального условия выбрать асимптотическое значе- ние x0 = 1 , то при небольших среднее сначала несколько увеличится,
а затем начинает асимптотически приближаться к x = 1 .

Средние значения |
91 |
Логистическое уравнение имеет устойчивую точку x1 = 1, при которой решение детерминированного уравнения dx = x(1 x) dt пере-
ста¼т изменяться. Для любого стохастического уравнения с небольшой волатильностью также можно изучить поведение решения в окрестности подобной особой точки. Так, в уравнении
dx = a(x) dt + b(x) W
разложим a(x) в ряд в окрестности x1, ãäå a(x1) = 0, а для b(x) возьм¼мнулевое приближение:
dx = a0(x1) (x x1) dt + b(x1) W;
где штрих производная по x.
Åñëè a0(x1) < 0, то это ни что иное, как уравнение Орнштейна-Уленбека,
имеющее при больших t следующее решение:
b(x1)
x(t) ! x1 + p ";
2a0(x1)
являющееся стационарным гауссовым процессом с средним
p
тильностью b1= 2a01.
Для логистического уравнения
x1 = 1; |
a0(x1) = 1; |
b(x1) = p |
2 |
; |
(3.16)
x1 è âîëà-
поэтому приближ¼нное решение в пределе больших врем¼н t ! 1 в соответствии с формулой (3.16) можно записать в следующем виде:
x(t) |
! |
1 + p "; |
(3.17) |
||
|
|
|
|
|
|
где " гауссово случайное число. Асимптотическое значение среднего равно 1, а дисперсия . Сравнивая эти значения с точными (3.13), мы видим, что (3.17) лишь первое приближение по .
К тому же, на самом деле, стационарная плотность вероятности для логистического блуждания - это гамма-распределение. Оно стремится к гауссовому только, когда параметр стохастического шума мал.
Таким образом, использовать решение Орнштейна - Уленбека для нелинейных уравнений, имеющих детерминированное стационарное решение, можно только в предположении малости стохастического воздействия. Тем не менее, подобный способ изучения поведения решения очень полезен, особенно в многомерном случае.

92 |
Глава 3. |
3.4Ряды для средних по степеням t
Решение обыкновенного дифференциального уравнения можно представлять в виде ряда по степеням t. Аналогично будем поступать и в
стохастическом случае, однако в ряд разложим непосредственно средние величины.
Для уравнения Ито:
dx = a(x; t) dt + b(x; t) W
возьм¼м первую итерацию от начального условия x0 = x(t0):
p
x = x0 + a(x0; t0) (t t0) + b(x0; t0) " t t0:
Учитывая " = 0 è "2 = 1, вычислим, с точностью до линейного приближения по t t0, среднее значение и среднее квадрата:
x = x0 + a(x0; t0) (t t0) + :::
x2 |
= x02 + 2x0 a(x0; t0) + b2(x0; t0) (t t0) + ::: |
Соответственно, дисперсия процесса в этом приближении будет равнаx2(t) = b2(x0; t0) (t t0) + ::. Чтобы получить дальнейшие члены разло-
жения, воспользуемся динамическим уравнением для средних.Для определ¼нности рассмотрим логистическое уравнение:
p
dx = x (1 x) dt + 2 x W:
В этом случае:
x |
|
= |
x0 |
+ x0 (1 x0) t + f t2 + ::: |
||||
x2 |
= |
x02 |
+ 2 x02 |
(1 |
|
x0) + x02 |
t + ::: |
|
|
|
|
|
|
|
|
|
|
Найд¼м коэффициент f. Для этого подставим разложения в уравнение для среднего:
_ 2 x = x x ;
ограничившись первым порядком по t:
x0 (1 x0) + 2 f t + ::: = x0 (1 x0) + x0 1 (3 + 2 )x0 + 2x20 t + :::;
откуда:
2 |
f = 1 (3 + 2 )x0 + 2x02: |
x0 |
Аналогично находятся следующие коэффициенты разложения.
Средние значения |
93 |
Найд¼м рекуррентные соотношения для произвольного члена разложения. Выбирая в (3.3), ñòð. 78, функцию F (x) = xn, запишем систему связанных дифференциальных уравнений:
x_n = (n + n (n 1) ) xn n xn+1 ;
Разложим средние в степенной ряд:
xn |
|
= x0n |
1 + fn;1 t + fn;2 t2 |
+ ::: |
= x0n |
1 |
#: |
|
"1 + fn;k tk |
||||||
|
|
|
|
|
Xk |
|
|
|
|
|
|
|
|
=1 |
|
Подставляя его в уравнение для средних и приравнивая коэффициенты при одинаковых степенях t, получаем при k = 1; 2; ::: систему рекуррент-
ных уравнений (fn;0 = 1):
k fn;k = n (1 + (n 1) ) fn;k 1 nx0 fn+1;k 1:
На системе аналитических расч¼тов Matematica фирмы Wolfram Research, Inc. вычисления среднего с точностью до t5 можно записать так:
f[n_ , 0] |
:= |
1; |
f[n_ , k_ ] |
:= |
(n/k )*((1+( n -1)* g )* f[n ,k -1] - x0 *f[n+1 ,k -1]); |
av = x0 ; Do [ av += x0 *f[1 , k ]* t^k , {k , 1, 5}]; Collect [av , t , Simplify ]
Первые две строки представляют собой рекурсивное определение функции f. Затем в цикле Do происходит суммирование разложения по t.
Последняя строка осуществляет вывод результата, сгруппированного в виде множителей при tn, к каждому из которых применяется операция
упрощения.
Заметим, что для большого числа членов разложения более быстрой будет нерекурсивная реализация программы:
f[n_ , 0] := 1; num = 5;
Do [
Do [
f[n ,k] = (n/k )*((1+( n -1)* g )* f[n ,k -1] - x0 *f[n+1 ,k -1]) , {n , 1, num -k +1}] ,
{k , 1, num }]
av = x0 |
; Do |
[ av |
+= x0 *f[1 , k ]* t^k , {k , 1, num }]; |
Collect |
[av , |
t , |
Simplify ] |
где в двойном цикле по k и n происходит явное вычисление коэффи-
циентов fn;k. Хотя и рекурсивную реализацию можно ускорить, написав: f[n_, k_]:=f[n,k]=(n/k) ...
94 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Глава 3. |
|||
|
|
Привед¼м первые три члена разложения: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
t2 |
|
|
|
|
|
|
||
|
|
|
|
|
= |
1 + 1 x0 t + 1 (3 + 2 )x0 |
+ 2x02 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
x0 |
2! |
|
t3 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
+ |
1 (7 + 10 + 4 2) x0 + (12 + 16 ) x02 26x03 |
|
+ ::: |
|
||||||||||||||||
|
2 |
(t) |
|
|
|
3! |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
t2 |
|
x(t) = x |
2 |
x |
: |
|
|
|
t3 |
||||||||
Аналогично для дисперсии процесса |
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
x |
|
= t + 4 + 2 |
|
6x0 |
|
|
|
+ 12 + 12 + 4 2 |
|
(48 + 46)x0 + 38x2 |
|
|
+ ::: |
||||||||||||
|
2 x02 |
|
2! |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
3! |
||||||||||
Подобным образом получаются разложения для моментов произвольного порядка. Выражения несколько упрощаются, если в качестве начального условия выбирается точка детерминированного асимптотического равновесия x0 = 1. При = 0 в этом случае решение не зависит от времени. В стохастической системе оно должно проэволюционировать к
ствует: |
x0 |
! x 1 = 1 : Поэтому зависимость от времени суще- |
|||||||||||||||||||||
значению: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
hxi 1 |
|
= |
|
|
t2 |
+ (3 |
|
2 ) |
t3 |
|
(7 |
|
38 + 4 2) |
t4 |
|
|
|
|||||
|
|
|
|
|
|
|
|||||||||||||||||
|
2 |
|
|
|
2! |
|
3! |
|
|
|
|
4! |
|
|
|||||||||
|
|
|
|
|
+ |
(15 |
334 + 284 2 8 3) |
t5 |
|
|
|
|
|
||||||||||
|
|
|
|
|
5! |
|
|
|
|
t6 |
|||||||||||||
|
|
|
|
|
|
|
|
|
2146 + 7012 2 1848 3 |
+ 16 4) |
|||||||||||||
|
|
|
|
|
(31 |
|
+ ::: |
||||||||||||||||
|
|
|
|
|
6! |
||||||||||||||||||
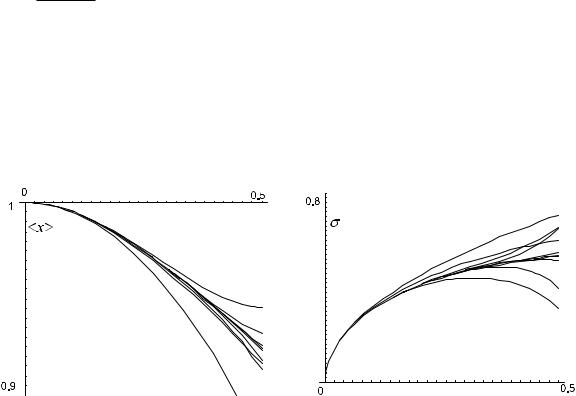
Графики разложений ( = 1=2) различного порядка (от k = 1 до k = 10) для среднего (слева) и волатильности (справа) имеют вид:
Подобные степенные разложения часто являются асимптотическими рядами и хорошо работают только при малых временах. Однако их сходимость можно улучшать при помощи различных методов, например, аппроксимацией Падэ.

Средние значения |
95 |
Естественно, можно строить разложения не только в виде ряда по t. Достаточно универсальным является метод последовательных при-
ближений. Его идея в следующем. Выберем некоторые функции n;0(t), являющиеся нулевым приближением для xn , òàê, ÷òî n;0(0) = xn0 . Ïîä- ставляя их в правые части уравнений для средних, получаем дифферен-
циальные уравнения. Решая их, мы найд¼м более точное приближение для функции xn = n;1(t). При повторении этой процедуры будет по-
лучаться вс¼ более точное выражение для средних. При этом на каждой итерации необходимо использовать начальное условие n;k(0) = xn0 . ×åì
удачнее выбор n;0(t), тем быстрее будут сходиться к точному значению последовательные приближения, и тем шире диапазон t для их применимости.
Рассмотрим логистическое уравнение:
x_n = n (1 + (n 1) ) xn n xn+1 :
В простейшем случае можно выбрать n;0(t) = xn0 . Тогда в первом при- ближении:
_n;1 = n (1 + (n 1) ) xn0 nxn0+1;
откуда:
n;1 = xn0 + xn0 [1 + n(1 x0) + n(n 1) ] t;
и т.д. В результате снова получаются степенные ряды по t, в которых коэффициенты разложения единым образом выражаются через n для любого xn .
Другой вариант выбора нулевого приближения n;0 = xn0 e nt. Â ýòîì случае:
n;1 = xn0 + xn0 [1 + (n 1) ] 1 e nt n +n 1 xn0+1 1 e 2nt :
В качестве нулевого приближения можно выбрать решение детерминированного уравнения. Тогда последовательно получаемые приближения окажутся рядами по величине волатильности стохастического шума .

96 |
Глава 3. |
3.5Квазидетерминированное приближение
Рассмотрим одномерное уравнение Ито:
dx = a(x; t)dt + b(x; t) W
в котором из функции b(x; t) явным образом выделен параметр волатильности процесса . Его мы будем считать малым. Пусть функция c(t) является решением детерминированного уравнения:
c = a(c; t): |
(3.18) |
Введ¼м новый процесс отклонения от детерминированного решения:
z = x c(t):
В силу Леммы Ито он удовлетворяет уравнению:
dz = 1 [a(c + z; t) a(c; t)] dt + b(c + z; t) W;
где вместо c мы подставили правую часть уравнения (3.18).
Запишем уравнение для средних (3.3), ñòð. 78, выбрав F = zn:
z_n |
n zn |
|
1 |
a c |
z; t |
a c; t |
)] + |
n(n |
1) |
z |
n |
2b2 |
|
c |
|
z; t : |
|
|
|
|
|
|
|
|
|
||||||||||
= |
|
|
|
[ ( + |
) |
( |
2 |
|
|
|
2: |
( |
|
+ |
) |
||
Разложим в ряд Тейлора по параметру функции a и b |
|
|
|
|
|||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
Xk |
|
|
|
|
|
a(c + z; t) = |
Ak(t) ( z)k; |
b2(c + z; t) = |
|
Dk(t) ( z)k: |
|||||||||||||
|
|
|
|
k=0 |
|
|
|
|
|
|
|
|
=0 |
|
|
|
|
Детерминированное решение c(t) нам известно и определяет функции времени Ak = Ak(t), Dk = Dk(t). Òàê êàê A0 = a(c(t); t), то в квадратных скобках уравнения для средних коэффициент A0
имеем:
z_n |
1 |
nAk+1 |
zn+k |
|
+ n(n2 1) Dk |
zk+n 2 |
|
k: |
(3.19) |
||||
= k=0 |
|||||||||||||
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
Разложим в ряд по степеням средние значения: |
|
|
|
||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
zn |
|
= |
|
zin(t) i |
|
|
|
(3.20) |
|
|
|
|
|
|
|
|
=0 |
|
|
|
|
|
|
В коэффициентах zn |
|
|
Xi |
|
|
|
|
||||||
n это верхний индекс, а не степень! Заметим, что |
|||||||||||||
|
|
i , |
|
|
|
|
|
|
|
|
|
|
|
1 = 1, откуда zi0 = 0 ïðè i > 0 è z00 = 1.
Средние значения |
97 |
Подставим разложение (3.20) в уравнение (3.19). В результате:
1 |
1 |
k+i: |
|
|
i=0 zin(t) i = k;i=0 n Ak+1 zin+k + n(n2 1) Dk zik+n 2 |
|
|
||
X |
X |
i = i0 |
|
k0, |
В двойной сумме в правой части сделаем замену индексов |
||||
k = k0. Òàê êàê i > 0, òî k0 < i0. Приравнивая члены при |
|
|
||
|
|
одинаковых |
||
степенях и опуская штрихи у индексов, получаем систему уравнений:
i |
n Ak+1 zin+kk + n(n2 1) Dk zik+kn 2 : |
(3.21) |
||
zin(t) = k=0 |
||||
X |
|
|
|
|
Выпишем несколько е¼ первых уравнений:
z01(t) = A1 z01
z02(t) = 2A1 z02 + D0 z03(t) = 3A1 z03 + 3 D0 z01 z04(t) = 4A1 z04 + 6 D0 z02
:::
z11(t) = A1 z11 + A2 z02
z12(t) = 2A1 z12 + 2A2 z03 + D1z01
z13(t) = 3A1 z13 + 3A2 z04 + 3D0 z11 + 3D1z02
:::
z21(t) = A1 z21 + A2 z12 + A3 z03
z22(t) = 2A1 z22 + 2A2 z13 + 2A3 z04 + D1z11 + D2z02
:::
z31(t) = A1 z31 + A2 z22 + A3 z13 + A4 z04; :::
Так как начальные условия учтены в детерминированном решении x0 =
c(t0), то для процесса z(t) они имеют вид z(t0) = 0. Соответственно равны нулю и все средние zn ïðè t = t0. Систему уравнений (3.21) можно решать как аналитически, так и численно, используя конечные приращения для производных по времени.
Если в задаче при t ! 1 возможен стационарный режим, в котором
zin = 0, то, приравняв левые части уравнений к нулю, получим систему с постоянными коэффициентами Ak = Ak(1), Dk = Dk(1), которая легко решается. В частности:
|
|
A2D0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 D1 |
|
D |
|
|
|
|
|
|
|
||||||
z |
= |
|
|
A2 |
|
::: |
|
|
|
|
|
|
|
|||
z2 |
= |
|
0 |
|
|
+ |
|
|
0 |
(D0(5A22 |
|
3A1A3) |
|
3D1A1A2 + D2A12) 2 |
+ ::: |
|
2A1 |
|
|
4A14 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||
Особенно удобен этот способ вычисления средних в многомерном случае, когда стационарное уравнение Фоккера-Планка решить сложно.
98 |
Глава 3. |
В качестве примера рассмотрим сначала точно решаемую задачу логарифмического блуждания:
dx = x dt + x W:
Как известно (стр. 58), средние значения имеют вид:
|
|
2 |
|
|
4t2 |
|
x = x0 e t; |
x2 |
= x02 e2 t+ |
t = x02e2 t |
1 + 2t + |
|
+ ::: : |
2 |
||||||
Так как уравнение линейно по x, детерминированное решение c(t) совпа-
дает с выражением для среднего. Ненулевые значения коэффициентов разложения сноса и дисперсии имеют вид:
A1 = ; D0 = x20 e2 t; D1 = 2x0e t; D2 = 1:
В результате ряды обрываются, и уравнения принимают вид:
zn = n zn + n(n 1) hx2 e2 t zn 2 + 2x0e t zn 1 + zn i:
i i 2 0 i i 1 i 2
Среднее значение (n = 1) для любой i-й поправки удовлетворяет урав-
нениям z1 |
= z1 |
|
|
z(0) = 0, òî âñå z1 = 0, и, следовательно, |
||||||
i |
|
|
i . Òàê êàê |
|
|
|
i |
|
||
x = c(t) = x0 e t. Для среднего квадрата: |
|
|
|
|||||||
|
z2 |
= 2 z2 |
+ x2 e2 t |
=> |
z2 |
= x2e2 t t |
|
|||
|
0 |
|
0 |
|
0 |
|
|
0 |
0 |
|
|
|
|
z2 = 2 z2 |
|
=> |
z2 |
= 0 |
|
||
|
|
|
1 |
|
1 |
|
|
1 |
|
|
|
|
z2 |
= 2 z2 |
+ z |
2 |
=> |
z2 |
= x2e2 t t2 |
=2; ::: |
|
|
|
2 |
|
2 |
0 |
|
0 |
0 |
|
|
Âитоге получаем разложение в ряд по точного решения.
Найд¼м теперь стохастические поправки к детерминированному решению для более сложного логистического уравнения:
dx = x (1 x) dt + x W:
Его детерминированное решение имеет вид (см. стр. 10): c(t) = 1 e t 1;
ãäå = 1 x0 1. Ненулевые коэффициенты разложения сноса и дисперсии равны:
A1 = 1 2 c(t); |
A2 = 1; D0 = c2(t); D1 = 2 c(t); D2 = 1: |
В асимптотическом пределе t ! 1 детерминированное решение c(t) стремится к единице, и полученные выше выражения для hzi, z2 âîñ- производят точные значения для среднего и волатильности (3.13), còð.89.

Средние значения |
99 |
В произвольный момент времени первое уравнение системы для средних (3.21) имеет вид:
z01(t) = 1 2c(t) z01(t) => z01(t) = (1 e t)2 :
Так как z(0) = 0, то, следовательно, константа интегрирования z0 ðàâ- на нулю, и, соответственно, поправка к z, пропорциональная , также
равна нулю z01(t) = 0. Аналогично равны нулю z13(t) = z12(t) = z21(t) = 0. Ведущий член для z2 подчиняется уравнению
z02(t) = 2 1 2c(t) z02(t) + c2(t);
решение которого с начальным условием z02(0) = 0 имеет вид:
z2 |
(t) = |
1 4 e t + (2 2 t + 4 1)e 2t |
: |
|
|||
0 |
|
|
|
|
2(1 e t)4 |
|
|
|
z |
|
|
|
|
||
Четв¼ртая степень |
|
â |
z04(t) = 3 z02(t) 2 : |
z0: |
|||
|
|
4 |
|
|
нулевом приближении выражается через |
2 |
|
Наконец, первая поправка к среднему значению равняется:
z1(t) = |
|
1 2(1 + (t 1))e t + (1 2 )e 2t |
: |
|||
1 |
2(1 |
|
|
t)3 |
|
|
|
e |
|
||||
Дальше члены разложения становятся достаточно громоздкими. Привед¼м их вид, когда = 0, т.е. начальное значение стохастического процес-
са стартует с асимптотически равновесного уровня x = 1. В этом случае среднее значение для x с точностью до 4 равно:
|
2 |
|
|
4 |
||
hxi = 1 1 e t 2 |
|
+ e t 2 3e t 2t 3 + 4e t e 2t |
|
: |
||
2 |
4 |
|||||
Аналогично для среднего квадрата: |
|
|
|
|
||
x2 = 1 1 4e t + 3e 2t |
2 |
|
|
|||
|
+ ::: |
|
|
|||
2 |
|
|
||||
Мы видим, что сложность аналитических выражений достаточно быстро увеличивается. Для практических целей иногда имеет смысл использовать численное решение системы дифференциальных уравнений. В этом случае при небольших мы будем получать средние значения быстрее,
чем при использовании Монте-Карло моделирования.
100 |
Глава 3. |
