
- •Случайные события
- •Стохастический мир
- •Случайные величины
- •Совместная и условная вероятности
- •Зависимость и независимость
- •Характеристическая функция
- •Модель аддитивного блуждания
- •Случайные процессы
- •Стохастические уравнения
- •Уравнение Ито
- •Остановка перед восхождением
- •Лемма Ито
- •Точные решения
- •Простые стохастические модели
- •Представление решений
- •Автокорреляция и спектр
- •Порождающий процесс Винера
- •Средние значения
- •Динамическое уравнение для средних
- •Процесс Феллера
- •Логистическое уравнение
- •Вероятности
- •Марковские плотности вероятности
- •Граничные условия
- •Стохастические интегралы
- •Площадь под траекторией Винера
- •Интегралы Ито
- •Интегрирование стохастических уравнений
- •Единственность решений
- •Метод последовательных приближений
- •Системы уравнений
- •Скоррелированные блуждания
- •Системы стохастических уравнений
- •Стохастический осциллятор
- •Линейные многомерные модели
- •Многомерие помогает одномерию
- •Как решать стохастические задачи?
- •Стохастическая природа
- •Теория броуновского движения
- •Стохастический осциллятор
- •Дрожание земной оси
- •Электронный шум
- •Хищники и их жертвы
- •Стохастическое общество
- •Финансовые рынки
- •Эмпирические закономерности
- •Диверсификация
- •Портфель на всю жизнь
- •Опционы
- •Кривая доходности
- •Компьютерное моделирование
- •Статистики
- •Случайные числа
- •Моделирование стохастических процессов
- •Ошибки вычислений и ускорение сходимости
- •Вычисление средних
- •R: Стохастический справочник
- •Основные соотношения теории
- •Системы уравнений с одинаковым шумом
- •M: Математические приложения
- •H: Помощь
- •C: Примечания
- •Рекомендуемая литература

64 |
Глава 2. |
2.6Представление решений
Мы записываем решения стохастических уравнений с начальным
условием x0 = x(t0) при помощи одной или нескольких случайных вели- чин " и гладкой функции времени: x(t) = f(x0; t0; t; "). Так как свойства " обычно хорошо известны, такое представление позволяет легко
находить разнообразные средние и марковскую плотность условной вероятности P (x0; t0 ) x; t).
Сама по себе функция f не позволяет нарисовать одиночную траекторию. Если мы сгенерим некоторое конкретное число "~, то x(t) не будет графиком случайного процесса. Это обычная гладкая функция. Напри-
мер, для винеровского процесса без сноса: |
|
||
p |
|
|
(2.33) |
|
|||
x(t) = x0 + " t t0: |
|
||
Никаких изломов, типичных для случайного процесса, тут, конечно, нет. Дело в том, что для получения свойств x(t) в каждый момент времени
необходимо генерить различные случайные числа ".
Тем не менее, благодаря марковости процессов начальные условия (x0; t0) могут быть значением случайной функции на любом этапе эволюции. В частности, мы можем записать следующую цепочку решений:
x1 = f(x0; t0; |
t1; "1) |
x1 |
|
|||
1 |
x3 |
|||||
x2 |
= f(x1; t1; |
t2 |
; "2) |
|||
2 |
||||||
x0 |
3 |
|||||
x3 |
= f(x2; t2; |
t3 |
; "3); :::; |
|||
|
||||||
x2 |
|
|||||
где интервалы времени ti ti+1 произвольны. Так как случайные переходы от одного момента времени (xi; ti) к следующему (xi+1; ti+1) íå ïå- рекрываются, случайные числа "1, "2, "3,.. являются статистически независимыми. Это позволяет вычислять средние, относящиеся к различным моментам времени, и строить выборочные траектории. При этом возникают последовательности вложенных функций, например:
x2 = f(f(x0; t0; t1; "1); t1; t2; "2):
В случае винеровского блуждания, выбирая равный интервал между последовательными моментами времени, мы получим:
Xt p xt = x0 + "k :
k=1
Хотя выражение для xt похоже на итерационную схему, это, на самом деле, точное соотношение, и может быть сколь угодно большим.
Стохастические уравнения |
65 |
Существуют и другие способы представления траектории случайно-
го процесса. Рассмотрим для примера разложение Палея-Винера винеровского блуждания на интервале времени t = [0::T ]:
|
t p |
|
1 |
sin( k t=T ) |
|
(2.34) |
||
|
|
|
||||||
|
|
|
|
|
Xk |
|
|
|
|
|
|
|
|
|
|
|
|
x(t) = x0 + "0 pT + 2T |
"k |
k |
; |
|
||||
|
|
|
|
|
=1 |
|
|
|
ãäå "k N(0; 1) независимые нормально распредел¼нные случайные величины. Это разложение имеет такие же статистические свойства ,
как и существенно более простая запись (2.33). Чтобы в этом убедиться, вычислим среднее квадрата x2 (простое среднее равно hxi = x0):
|
|
|
t2 |
1 |
sin2( k t=T ) |
|
|
|
|||
|
|
|
Xk |
|
|
|
|||||
x2 |
|
= x02 + |
|
+ 2T |
|
|
|
|
= x02 |
+ t; |
(2.35) |
|
|
|
T |
=1 |
|
2k2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
где мы воспользовались свойством независимости h"i"ji = 0, åñëè i 6= j
è "2i = 1. Равенство x2 = x20 + t проверяется при помощи фурье разложения функции f(t) = t t2=T на интервале t = [0::T ] (l H16).
В результате получается такой же результат, как и для (2.33). Плотности вероятности величин (2.33) è (2.34) совпадают, так как сумма гаус- совых чисел "0,"1,... это опять гауссово число, дисперсия которого, как
мы показали, равна t.
Достоинством представления Палея-Винера является то, что с его помощью можно записывать непрерывную функцию одиночной траектории, на конечном интервале времени T . Для этого, естественно, прихо-
дится обрезать суммирование на достаточно большом индексе k = N.
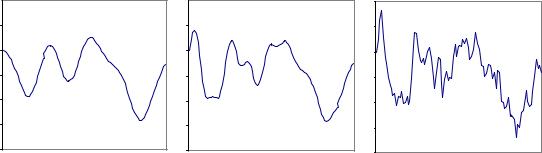
Затем генерятся независимые случайные числа "0,...,"N , и фурье раз- ложение да¼т изломанную кривую. На рисунках ниже приведено последовательное увеличение числа слагаемых в сумме: N = 10; 20; 100. При
этом случайные числа "0, "1,.. на каждом графике повторяются:
N=10 |
N=20 |
N=100 |
Видно, что степень изломанности траектории увеличивается, стремясь в пределе N ! 1 к недифференцируемой стохастической кривой.
66 |
Глава 2. |
Изучая стохастические дифференциальные уравнения, можно ис-
пользовать различный язык и различные математические конструкции. Кратко перечислим основные подходы к представлению решений стохастических уравнений, их сильные и слабые стороны.
B Плотность вероятности является базовым и наиболее общим язы-
ком описания случайных функций. Так как мы ограничились классом марковских процессов, знание вероятности перехода P (x0; t0 ) x; t) между двумя точками позволяет записать вероятность всей траектории. В результате можно вычислять разнообразные средние, и т.п. Чтобы найти P (x0; t0 ) x; t), необходимо решить дифференциальное уравнение в частных производных, которое мы рассмотрим в четв¼ртой главе. Недостатком этого подхода является то, что получение конечного результата иногда требует более кропотливых вычислений, чем в рамках других методов. Примером тому служит описание процесса Орнштейна-Уленбека или процесса Феллера (стр. 82).
B Уравнения для средних мы рассмотрим в следующей главе. Если
целью исследования является поиск различных средних значений стохастического процесса, то решение этих уравнений может оказаться самым прямым и простым способом. Дифференциальные уравнения для средних часто приводят к полезным соотношениям в асимптотическом пределе t ! 1 и удобны при построении приближ¼нных методов. Кроме
ограниченности получаемых результатов, недостаток подхода в том, что эти уравнения оказываются замкнутыми лишь для относительно узкого класса задач.
B Сведение к известному процессу является очень распростран¼нным подходом. Обычно при этом используется винеровский процесс W (t) с хо-
рошо изученными и простыми свойствами. Например, логарифмическое блуждание x(t) = x0 expf( 2=2)t + W (t)g явным образом демон-
стрирует деформацию винеровского процесса W (t) в процесс x(t). По-
добные решения ищутся при помощи леммы Ито и подходящей замены. Достоинством подхода является быстрота получения конечного результата (когда это возможно). Кроме этого, мы имеем простую запись для выборочных траекторий. Например, можно сгенерить конкретную тра-
екторию W (t) и, подставив е¼ в x t; W (t) , получить выборочную траек- торию процесса x(t). Недостатком подхода является то, что для многих
не очень просто. Так, уже для процесса Орнштейна-Уленбека в аргументе функции W (t) необходи-
мо дополнительно деформировать время, а процесс Феллера вообще не имеет простого представления при помощи W (t).
Стохастические уравнения |
67 |
B Стохастические интегралы это наиболее популярный способ как
строгого обоснования стохастических уравнений, так и записи их решения при помощи специфических обозначений. Стохастические интегралы являются достаточно нетривиальной математической конструкцией. Несмотря на то, что это очень красивая и мощная техника, иногда получаемые с е¼ помощью результаты оказываются формальными, и воспользоваться ими для вычисления, например, средних или плотности вероятности не представляется возможным. Мы будем обсуждать стохастическое интегрирование в пятой главе.
B Скалярные случайные величины широко используются в этой книге. Стохастичность функции x(t) можно придать при помощи обычной случайной величины ", не являющейся процессом, и гладкой функции времени. Величина " имеет определ¼нное распределение. Чаще всего оно
гауссово, однако в общем случае это не обязательно. Дальше мы увидим, что простую форму решению для некоторых процессов можно придать, только используя две или более случайные величины, имеющие совместную плотность вероятности. Запись решения в виде x = f(x0; t0; t; ")
позволяет легко находить различные средние. Кроме этого, функция f
эквивалентна заданию в неявной форме марковской плотности вероятности P (x0; t0 ) x; t). Действительно, при помощи среднего от произволь-
ной функции F (x) можно сделать преобразование, например, от гауссовой переменной " к x (значения начальных условий x0, t0 опущены):
1 |
1 |
|
|
hF (x)i = Z |
F (x) P (x; t) dx = Z |
F f("; t) |
P (") d"; |
1 |
1 |
|
|
где P (") распределение Гаусса. Проводя во втором интеграле обратную замену x = f(t; "), мы переходим к первому интегралу, и, следовательно, плотность вероятности случайного процесса в момент времени t равна:
P (x0; t0 |
) x; t) = p2 |
@x |
exp |
2 g2 |
(x; t) |
; |
(2.36) |
|
1 |
@g(x; t) |
|
1 |
|
|
|
где g(x; t) обратная к x = f(t; ") функция, т.е. " = g(x; t).
В заключение выскажем очевидную истину. Использование того или иного языка должно диктоваться в первую очередь соображением простоты. В зависимости от того, какие задачи решаются, более адекватным может оказаться любой из перечисленных выше подходов.
