
emph_f
.pdf
силы, играющей важную роль при изучении гидродинамических процессов в океане, является сила Кориолиса. Речь о ней пойдет в п. 1.5.6.
Обратившись к анализу внутренних сил, заметим, что они существенно зависят от характера жидкости. Мы будем рассматривать в этом пункте идеальную жидкость, т. е. такую сплошную среду, в которой внутренние силы сводятся к давлению, причем независимо от того, находится ли среда
всостоянии равновесия или движения. Это означает, что если выделить
вжидкости некоторую область , ограниченную поверхностью , то действие на нее остальной части жидкости описывается силой, направленной
вкаждой точке x 2 по внутренней нормали. При этом сама величина p давления, приходящегося на единицу площади, зависит не от ориентации той бесконечно малой площадки, к которой давление приложено, а лишь от ее координат. Таким образом, на элемент поверхности dS в идеальной жидкости действует сила
pndS = (ip cos + jp cos + kp cos )dS; |
(5.8) |
где cos ; cos ; cos – направляющие косинусы внешней нормали n. Знак “ ” в (5.8) выбран в связи с тем, что положительное давление действует в направлении внутренней нормали. На всю область будет действовать сила, равная поверхностному интегралу
Z Z Z Z
pndS = i p cos dS + j p cos dS + k p cos dS ;
который с помощью формулы (4.3) можно свести к тройному интегралу
Z
rpdx: (5.9)
Формула (5.9) означает, что объемная плотность внутренних сил в идеальной жидкости равна rp. Из (5.9) и предыдущих результатов следует, что объемная плотность сил, действующих в идеальной жидкости, имеет вид
rp + f; |
(5.10) |
где f – массовая плотность всех внешних сил (например, силы тяжести, силы Кориолиса и т. д.). В проекциях на оси координат (5.10) имеет вид
|
@p |
+ fi; i = 1; 2; 3: |
(5.11) |
@xi |
Теперь мы в состоянии вывести уравнение, описывающее движение жидкости под действием сил с объемной плотностью (5.10). С этой целью подставим в (5.4) вместо произведение ui, а вместо q компоненту (5.11) силы (5.10). В результате получим уравнение
@ |
|
( ui) + div( uiu) = |
@p |
+ fi; |
|
|
|
||
@t |
@xi |
|||
41

которое можно переписать в виде |
@xj ( uj)#ui = @xi |
|
|
|||||||||
@ti + |
3 |
uj @xj |
+ "@t |
+ |
+ fi: |
(5.12) |
||||||
|
@u |
X |
|
@ui |
|
@ |
Xj |
@ |
|
@p |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
j=1 |
|
|
|
|
=1 |
|
|
|
|
|
В силу уравнения неразрывности (5.6) выражение в квадратных скобках в (5.12) обращается в нуль. В результате приходим к уравнениям
@ui |
3 |
|
@ui |
|
@p |
|
|
|||
Xj |
|
|
|
(5.13) |
||||||
|
|
|
|
|
|
|
|
|||
@t + |
uj @xj |
= @xi |
+ fi; i = 1; 2; 3 |
|||||||
=1 |
||||||||||
|
|
|
|
|
|
|
|
|
||
для компонент ui, эквивалентных следующему векторному уравнению:
|
@u |
+ (u r)u = rp + f: |
(5.14) |
@t |
Здесь через (u r)u обозначен вектор, имеющий размерность ускорения, называемый в гидродинамике конвективным ускорением. Компоненты его в декартовом базисе определяются формулами
3 |
@ui |
|
|
Xj |
; i = 1; 2; 3: |
||
|
|||
[(u r)u]i = uj @xj |
|||
=1 |
|
|
|
Уравнение (5.14) называется основным уравнением гидродинамики идеальной жидкости. Его также называют уравнением Эйлера в честь выдающегося ученого Леонардо Эйлера (1707–1783). Поскольку его вывод основан на интегральном законе сохранения импульса, то уравнение (5.14) называется также дифференциальным законом сохранения импульса.
Уравнения (5.5), (5.14) представляют собой систему четырех скалярных дифференциальных уравнений относительно пяти скалярных искомых функций: компонент u1; u2; u3 скорости u, давления p и плотности , т. е. они образуют незамкнутую (неполную) математическую модель. Для ее замыкания к (5.5), (5.14) следует присоединить еще одно скалярное уравнение. Для рассматриваемой нами идеальной жидкости в качестве такого уравнения можно использовать термодинамическое уравнение состояния, имеющее в простейшем случае вид
p = P ( ); |
(5.15) |
где P ( ) – заданная функция. В результате мы получим замкнутую систему пяти скалярных уравнений (5.5), (5.14) и (5.15) для пяти неизвестных u1; u2; u3; p и . Указанная система, называемая математической моделью идеальной баротропной жидкости, характеризует так называемую
42
однопараметрическую среду, т. е. среду, в которой все термодинамические величины зависят от одного параметра, в данном случае от плотности .
Более реалистичны двухпараметрические среды, для которых все термодинамические величины зависят от двух параметров, например, плотности и энтропии s. (О физическом смысле энтропии можно прочитать, например, в [30]). Для таких сред (5.15) следует заменить уравнением
p = P ( ; s); |
(5.16) |
а для замыкания системы (5.5), (5.14), (5.16) следует добавить еще одно уравнение для энтропии s. Указанное уравнение легко получается из общего закона сохранения (5.4), в котором следует положить = s; q = 0 (последнее условие объясняется отсутствием источников энтропии в идеальной жидкости). В результате приходим к уравнению
@s |
+ div(su) = 0; |
(5.17) |
|
@t |
|||
|
|
называемому уравнением адиабатичности и описывающему фактически сохранение энергии в идеальной жидкости. Уравнения (5.5), (5.14), (5.16), (5.17) образуют модель идеальной двухпараметрической жидкости.
Наряду с двухпараметрическими средами существуют среды, в которых давление зависит от трех и более параметров. Так, морскую воду, представляющую собой химический раствор, содержащий растворенные частицы соли и других веществ, можно считать трехпараметрической средой, в которой давление p будет зависеть не только от и энтропии s, но и от солености S. Поэтому для более точного описания гидродинамических процессов в океане уравнение (5.16) следует заменить на уравнение
p = P ( ; s; S); |
(5.18) |
а к системе (5.5), (5.14), (5.17), (5.18) следует добавить еще одно уравнение для S, получающееся из (5.4) при = S; q = FS, и имеющее вид
@S |
+ div(Su) = FS: |
(5.19) |
|
@t |
|||
|
|
Здесь FS – объемная плотность источников солей.
Приведенные выше модели описывают сплошные среды, характеризующие газы и сжимаемые жидкости. Многие среды, как, например, обычная вода, практически несжимаемы. Поэтому для замыкания математических моделей, описывающих такие среды, вместо уравнений состояния вида (5.15), (5.16), (5.18) добавляют условие несжимаемости жидкости
div u = 0: |
(5.20) |
43

В силу (5.20) и (4.20) уравнение (5.5) упрощается и принимает вид
@ |
+ u grad = 0: |
(5.21) |
@t |
Математическая природа уравнения 1-го порядка (5.21) такова (см. § 2.2), что его решения принимают постоянные значения на характеристиках уравнения (5.21), описывающих по своему физическому смыслу траектории частиц движущейся жидкости. Отсюда следует, что плотность несжимаемой жидкости сохраняется вдоль любой траектории (т. е. вдоль характеристики уравнения (5.21)), хотя и может изменяться при переходе от одной траектории к другой. С учетом последнего обстоятельства указанную жидкость называют неоднородной, а соответствующую систему уравнений (5.14), (5.20) и (5.21) называют моделью идеальной несжимаемой неоднородной жидкости. В важном частном случае, когда = const, жидкость называется однородной. Поскольку уравнение (5.21) тождественно выполняется при = const, то модель идеальной несжимаемой однородной жидкости состоит из четырех скалярных уравнений (5.14), (5.20) относительно четырех скалярных функций u1; u2; u3 и p.
Итак, выше мы вывели пять математических моделей, описывающих движение идеальной жидкости. Перечислим их: 1) модель M1 идеальной баротропной жидкости, состоящая из пяти скалярных уравнений (5.5), (5.14), (5.15); 2) модель M2 идеальной двухпараметрической жидкости, состоящая из шести уравнений (5.5), (5.14), (5.16) и (5.17); 3) модель M3 идеальной трехпараметрической жидкости, состоящая из семи уравнений (5.5), (5.14), (5.17), (5.18) и (5.19); 4) модель M4 идеальной несжимаемой неоднородной жидкости, состоящая из пяти уравнений (5.14), (5.20), (5.21) и 5) модель M5 идеальной несжимаемой однородной жидкости, состоящая из четырех уравнений (5.14), (5.20) при =const.
В заключение отметим, что все пять построенных моделей содержат дифференциальные уравнения лишь первого порядка. Это не случайно, а связано с тем фактом, что при их выводе мы пренебрегали действием эффектов вязкости, теплопроводности и химических реакций, которые описываются выражениями, содержащими производные второго и более высокого порядка от искомых функций. Таким образом, все построенные в п. 1.5.3 модели относятся к идеальной жидкости, в которой внутренние силы состоят из сил давления. В этом смысле все указанные модели описывают идеальный гидродинамический процесс по терминологии § 1.1.
1.5.4. Модели движения вязкой жидкости. Шестая проблема тысячелетия. Модели идеальной жидкости являются приближенными, поскольку в реальных жидкостях всегда присутствует трение, вызываемое наличием вязкости в жидкости. Наличие вязкости в жидкости приводит к возникновению дополнительной внутреней силы (препятствующей движе-
44

нию жидкости). В случае несжимаемой жидкости ее объемная плотность часто моделируется выражением (см., например, [40]):
u: (5.22)
Здесь u – векторный лапласиан от скорости u, определяемый, в частности, в декартовом базисе формулой u = ui+ vj+ wk, – постоянный коэффициент динамической вязкости, имеющий размерность [ ] =кг/м с. В общем случае может зависеть как от точек x 2 D, так и от некоторых характеристик среды, например, температуры, причем выражение для силы вязкого трения имеет более сложный вид, чем в (5.22) (см., например, [40]). Однако рассмотрение более сложных моделей выходит за рамки данной книги. Добавив выражение (5.22) в правую часть основного уравнения движения идеальной жидкости (5.14), приходим к уравнению
|
@u |
+ (u r)u = rp + u + f; |
(5.23) |
@t |
представляющему собой основное уравнение динамики вязкой жидкости. Оно называется векторным уравнением Навье-Стокса в честь французского инженера A. Navier (1785–1836) и английского физика G.G. Stokes (1819–1903), много сделавших для становления и развития гидродинамики вязкой жидкости.
Заменив в моделях M4 и M5 идеальных жидкостей уравнение движения идеальной жидкости (5.14) уравнением (5.23), мы получим две математические модели, описывающие движение вязкой несжимаемой жидкости: модель M6 вязкой неоднородной жидкости и модель M7 вязкой несжимаемой однородной жидкости. Они описываются соответственно уравнениями:
|
@u |
+ (u r)u = rp + u + f; div u = 0; |
@ |
+ u r = 0; |
|||
|
|
|
|||||
@t |
@t |
||||||
|
|
|
@u |
+ (u r)u = rp + u + f; div u = 0; |
= const: |
||
|
|
|
|||||
|
|
@t |
|||||
Последняя модель, называемая моделью Навье-Стокса, является одной из важнейших моделей в гидродинамике вязкой несжимаемой жидкости.
Наряду с приведенными моделями движения вязкой жидкости существует еще большое количество других моделей, в которых кроме сил вязкого трения учитываются и другие эффекты, описываемые дифференциальными операторами второго порядка. Среди них различают модели теплопереноса, учитывающие действие в жидкости как сил трения, так и тепловых эффектов, модели массопереноса, учитывающие влияние на движение жидкости различных загрязняющих веществ, модели вязкой токопроводящей жидкости, учитывающие эффекты действия электромагнитных сил на проводящую жидкость, и т. д.
45

Ограничимся здесь приведением трех математических моделей. Первая модель описывает движение вязкой однородной несжимаемой теплопроводной жидкости. Предварительно отметим, что наличие градиента температуры в жидкости приводит к возникновению в ней дополнительной объемной силы. Чтобы вывести выражение для ее плотности, рассмотрим область D, в которой находится жидкость с постоянными плотностью 0 и температурой T0. Предположим, что после нагревания либо охлаждения некоторой подобласти области D плотность и температура жидкости встановятся равными и T . Тогда на жидкость в области со стороны оставшейся жидкости будет действовать сила, имеющая смысл силы плавучести с объемной плотностью, равной ( 0)g. Если разность 0 мала по сравнению с 0, то термодинамическое уравнение состояния жидкости может быть приближенно записано в виде = 0 0 T (T T0) [15, с.264]. Здесь параметр T > 0, называемый объемным коэффициентом теплового расширения, имеет размерность K 1, где K – сокращенное обозначение Кельвина как единицы температуры. Он так назван в честь знаменитого английского физика W. Thomson (1824–1907), получившего в 1892г. за выдающиеся научные заслуги титул барона Кельвина (Kelvin). С учетом указанного приближения объемную плотность fT силы плавучести можно записать в виде
fT = 0 T (T T0)g: |
(5.24) |
Выражение (5.24) следует добавить в уравнение (5.23), в котором следует положить = 0. Поскольку в (5.24) входит неизвестная в общем случае температура T , то для построения замкнутой модели к построенной системе уравнений необходимо присоединить соответствующее уравнение для T . В качестве последнего можно взять уравнение (5.21) при = 0, c = const и k = const. В результате приходим к следующей модели:
@u
0 @t + 0(u r)u = rp + u + 0f 0 T (T T0)g; divu = 0;
0c |
@T |
= k T u rT + F; 0 = const: |
(5.25) |
@t |
Модель (5.24) описывает процесс движения вязкой несжимаемой теплопроводной жидкости. Указанная модель называется моделью тепловой конвекции. Данная модель была выведена нами при использовании так называемого приближения Буссинеска. Согласно этому приближению изменения плотности в жидкости, вызываемые наличием градиентов температуры, учитываются в соответствии с термодинамическим уравнением состояния лишь в записи дополнительной объемной силы – силы плавучести, в виде (5.25). Кроме того, коэффициенты , k и c считаются постоянными. Модель (5.24) также называют моделью Обербека–Буссинеска по именам
46

известного французского механика и физика J.V. Boussinesq (1842–1929) и немецкого физика A. Oberbeck (1846–1900).
В качестве второй модели выведем модель переноса вещества (например, загрязняющей примеси) в вязкой несжимаемой жидкости. Как и выше, воспользуемся приближением Буссинеска. Согласно ему коэффициенты вязкости и диффузии и считаются константами, тогда как сила плавучести, возникающая за счет изменения плотности среды, вызываемого наличием вещества с концентрацией C, является линейной функцией от C. Для вывода выражения этой силы рассмотрим область D жидкости постоянной плотности 0, в которой находится вещество с постоянной концентрацией C0. Предположим, что в некоторой части области D произошло изменение количества вещества, в результате чего плотность и концентрация приняли значения, равные и C. Тогда со стороны оставшейся жидкости на область будет действовать сила плавучести, объемная плотность которой равна ( 0)g. Если разность 0 мала, то уравнение состояния может быть записано в виде = 0 + 0 C(C C0) [15, с.264]. Здесь параметр C > 0, имеющий размерность м3=кг, носит название объемного коэффициента массового расширения жидкости. С учетом этого объемную плотность fC силы плавучести можно записать в виде
fC = 0 C(C C0)g: |
(5.26) |
Выражение (5.26) следует добавить в уравнение (5.23). Поскольку (5.26) содержит неизвестную в общем случае концентрацию C, то для замыкания соответствующей модели к ней необходимо присоединить уравнение для концентрации C. В качестве его следует взять уравнение (4.24) при = const. В результате приходим к следующей математической модели:
@u
0 @t + 0(u r)u = rp + u + 0f + 0 C(C C0)g; divu = 0;
@C |
= C u rC + FC; 0 = const: |
(5.27) |
@t |
Данная модель, называемая моделью переноса масс Обербека-Буссинеска, описывает процесс переноса вещества (или масс) в вязкой несжимаемой жидкости в приближении Буссинеска.
В случае, если перенос вещества происходит в теплопроводной жидкости, в которой существенны тепловые эффекты, возникают две силы плавучести: одна вызывается наличием вещества в жидкости, а другая – температурными эффектами. Добавив выражения (5.25) и (5.26) для этих сил в уравнение сохранения импульса (5.23) и присоединив к полученному уравнению соответствующие уравнения для температуры T и концентрации C и условие несжимаемости, приходим к еще одной математической модели:
@u
0 @t + 0(u r)u = rp + u + 0f 0[ T (T T0) C(C C0)]g;
47

c |
@T |
= k T u rT + F; |
@C |
= C u rC + FC; div u = 0; (5.28) |
|
|
|||
@t |
@t |
называемой моделью тепло- и массопереноса в вязкой жидкости.
Замечание 5.1. Более строгий анализ показывает, что процесс переноса тепла в вязкой жидкости сопровождается переходом кинетической энергии жидкости в работу сил вязкого трения. Последнее приводит к появлению в жидкости дополнительного источника тепла, объемная плотность F которого определяется формулой [40, с.10]:
3 |
@ui |
|
@uj |
|
|
X |
|
(5.29) |
|||
|
|
|
|
||
F = 2 ( |
|
+ |
|
): |
|
@xj |
|
||||
i;j=1 |
|
@xi |
|
||
|
|
|
|
|
|
Здесь ui – компоненты скорости u, – коэффициент динамической вязкости, а F носит название диссипативной функции. С учетом этого более точная модель переноса тепла в движущейся жидкости имеет вид
@T
c @t = div(kgradT ) div(T u) + F + F :
Замечание 5.2. Отметим, что для выделения единственного решения приведенных здесь математических моделей необходимо задавать начальные и краевые условия. Подробное обсуждение различных формулировок начально-краевых задач для указанных моделей можно найти в цитируемых выше учебниках по гидродинамике и тепломассопереносу [15], [30], [40]. В частности, для модели Навье–Стокса (5.23) при = 0 = const, рассматриваемой в ограниченной области пространства R3, простейшая начально-краевая задача описывается соотношениями:
@u
0 @t + 0(u r)u = rp + u + 0f; div u = 0;
ujt=0 = u0(x) в ; uj = g(x; t); t 2 [0; T ]: |
(5.30) |
Здесь u0(x) и g(x; t) – заданные функции своих аргументов. Подчеркнем, что несмотря на кажущуюся простоту начально-краевая задача (5.30) даже при g = 0 является одной из сложнейших математических задач современности. Это связано с тем, что математики до сих пор не смогли установить функциональный класс, в котором удалось бы доказать глобальную (т.е. на любом интервале [0; T ] времени) разрешимость и единственность решения даже задачи Коши для уравнений Навье–Стокса, рассматриваемых во всем пространстве R3, не говоря уже о более сложной краевой задаче (5.30). Недаром она вошла под номером 6 в знаменитый список семи задач 21-го столетия (“Millennium Prize Problems”), за решение каждой из которых назначена награда в 1 миллион долларов. Более подробно об этом
48

можно прочитать на сайте американского математического института Clay Mathematics Institute (http://clay.math.org).
Замечание 5.3. Все приведенные выше модели описывают нестационарные движения жидкости. В случае, когда процессы движения жидкости являются стационарными, т. е. не зависят от времени, мы приходим к стационарным моделям движения жидкости. Они получаются из приведенных моделей отбрасыванием в исходных уравнениях слагаемых вида@u=@t, @ =@t, @s=@t и т. д. Детальный анализ разрешимости различного рода краевых задач для стационарных уравнений гидродинамики, тепломассопереноса и магнитной гидродинамики можно найти в [4,5].
1.5.5. Модель стационарного безвихревого движения несжимаемой жидкости. Рассмотрим стационарный процесс движения идеальной несжимаемой однородной жидкости под действием силы тяжести. Отвечающая этому случаю модель M5 принимает с учетом замечания 5.3 и условия f = g вид
(u r)u = |
1 |
(5.31) |
rp + g; divu = 0; = const: |
Используя известное векторное тождество (см. прил. 2)
(u r)u = rotu u + r
u2
2
и предполагая, что массовая сила является потенциальной, так что g = rG, где G – потенциал силы тяжести, перепишем (5.31) в виде
|
p |
|
u2 |
|
||
rotu u = r |
|
+ |
|
|
+ G ; divu = 0: |
(5.32) |
|
2 |
|||||
Важную роль на практике играют безвихревые течения идеальной жидкости. Для таких течений скорость u удовлетворяtт условию rot u 0, так что модель (5.31) принимает вид
|
|
|
|
|
rot u = 0; div u = 0; |
(5.33) |
|||||||
|
p |
|
u2 |
|
|
p |
|
u2 |
|
||||
r |
|
+ |
|
+ G |
= 0 ) |
|
|
|
+ |
|
|
+ G = const; = const: |
(5.34) |
|
2 |
|
2 |
||||||||||
Важно отметить, что гидродинамическая модель в данном случае разделилась, т. е. свелась к системе двух уравнений (5.33) для скорости u и уравнению (5.34)) для давления. Оно называется в гидродинамике уравнением или законом Бернулли [40] в честь швейцарско-голландского математика D.Bernoulli (1700–1782). Из закона Бернулли следует, что давление в безвихревом движении жидкости снижается при увеличении скорости ее
49
движения. Именно этот закон объясняет причину образования подъемной силы на крыльях летательных аппаратов.
Напомним, следуя [19, с.200], что трехмерная область D называется
поверхностно-односвязной (или просто односвязной), если для любой кусоч- но-гладкой замкнутой кривой D можно указать такую ориентируемую кусочно-гладкую поверхность в D, границей которой является . Известно (см. § 6.2 и [19, с. 200]), что условие rot u = 0 эквивалентно (по крайней мере для односвязных областей) условию потенциальности потока, т. е. существованию такой функции ', называемой потенциалом скорости, что u = grad'. Подставляя это соотношение во второе уравнение в (5.33), приходим с учетом (3.18) к уравнению Лапласа
div(grad') ' = 0 |
(5.35) |
для потенциала ', которое тем самым образует математическую модель стационарного безвихревого движения идеальной однородной несжимаемой жидкости. Решив его при соответствующих граничных условиях на границе области и на бесконечности, если – неограниченная область (см. об этом в § 1.3), мы найдем искомую скорость u по формуле u = grad '. Таким образом, выше построен пример еще одного физического процесса, а именно: стационарного потенциального течения идеальной несжимаемой жидкости, исследование которого сводится к решению краевой задачи для уравнения Лапласа.
1.5.6. Сила Кориолиса и элементы динамики океана. Другим важным примером внешней силы является сила Кориолиса, названная в честь французского ученого G.G. Coriolis (1792–1842). Указанную силу, возникающую вследствие вращения Земли, необходимо учитывать при рассмотрении гидродинамических процессов в океане. Согласно теории вращающихся тел массовая плотность fc силы Кориолиса определяется формулой [57, с.21]
fc = 2 u:
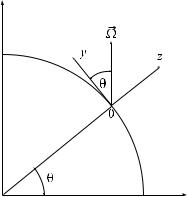
Здесь – вектор угловой скорости вращения Земли, направление которого совпадает с направлением оси Земли (с юга на север), а величина равна примерно 1:46 10 4 с 1. Предположим для определенности, что ось y направлена по касательной к поверхности Земли на север (см. рис. 5.1.), тогда как ось z направлена вертикально вверх. Ось x в таком случае будет направлена на восток, поскольку тройка единичных ортов i; j; k образует правый базис.
Из рис. 5.1 видно, что угол между осью y и направлением вектора в точке с широтой равен
(5.36) |
Рис. 5.1 |
50
