emph_f

телу массы m на Земле сообщена начальная скорость v0, направленная под углом к ее поверхности; требуется найти траекторию движения тела и вычислить расстояние между ее начальной и конечной точками.

Как и в [55], будем предполагать, что речь идет о камне, брошенном с помощью катапульты. Это уточнение определяет характерные размеры тела, его массу и возможную начальную скорость. Построим для данного случая математическую модель, основанную на следующих предположениях:

1)Земля – инерциальная система отсчета;

2)ускорение свободного падения g постоянно;

3)кривизной Земли можно пренебречь, считая ее плоской;

4)камень моделируется материальной точкой массы m, вылетающей с уровня Земли, причем действием воздуха на движущийся камень можно пренебречь.

Введем систему координат x; y с центром в точке вылета камня из катапульты, причем ось x направим горизонтально в сторону движения камня,

аось y – вертикально вверх. При сделанных предположениях движение камня будет описываться известным из школьного курса физики вторым законом Ньютона, названным так в честь великого английского математика, механика, физика, астронома и философа I. Newton (1643–1727). Указанный закон имеет вид

Здесь r(t) = x(t)i + y(t)j - положение камня в плоскости x; y в момент t, где i и j – единичные орты введенной (плоской) декартовой системы координат (декартова базиса), a = •r – ускорение движущейся точки, f –

вектор внешних сил и r = x i+ y j обозначает вторую производную по времени. Поскольку при наших предположениях на камень при его движении

где g = gj. Здесь g – ускорение свободного падения. Его величина на средних широтах равна 9.8 м/с2. Подставляя (2.2) в уравнение (2.1), записанное в проекциях на оси координат, и добавляя начальные условия, приходим к искомой математической модели рассматриваемого процесса, имеющей вид

Математически полученная модель представляет собой задачу Коши для системы двух обыкновенных дифференциальных уравнений 2-го порядка с постоянными коэффициентами. Указанная задача элементарно решается, а ее решение, как легко проверить, имеет вид

11

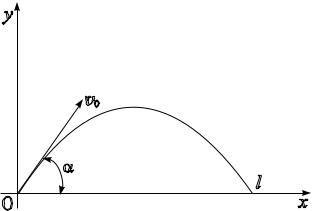
Физически соотношения (2.4) означают, что проекция камня на ось x будет двигаться равномерно со скоростью vx = v0 cos , тогда как проекция на ось y будет двигаться с постоянным ускорением ay = g, имея своей начальной скоростью vy = v0 sin . Выражая из первого уравнения в (2.4) время t через x и подставляя во второе уравнение (2.4), получаем искомое уравнение траектории камня. Оно имеет вид параболы (см. рис. 2.1):

Указанная парабола пересекает ось x в двух точках: x = 0 и x = l, где

Первая точка x = 0 является начальной точкой траектории, в ней камень вылетает из катапульты. Вторая точка соответствует месту падения камня на землю. Формула (2.6) и определяет в рамках принятой модели искомое расстояние l. Эта формула хорошо известна из школьного учебника по

кает тогда, когда наших знаний об изучаемом объекте недостаточно. В этом случае при построении матема-

тической модели приходится делать дополнительные предположения, или гипотезы. Выводы, полученные в результате исследования такой гипотетической модели, носят для изучаемого объекта условный характер. Они справедливы для него настолько, насколько правильны исходные предположения. Для их проверки необходимо сопоставить результаты исследования модели со всей имеющейся информацией об изучаемом объекте. Степень близости расчетных и экспериментальных данных позволяет судить о качестве гипотетической модели, о справедливости или ошибочности исходных предположений. Таким образом, вопрос применения некоторой модели к изучению рассматриваемого объекта не является чисто математическим

12

вопросом и не может быть решен лишь математическими методами. Основным критерием истинности является эксперимент или практика. Критерий практики позволяет сравнить различные гипотетические модели и выбрать из них такую, которая является наиболее простой и в то же время в рамках требуемой точности правильно передает свойства изучаемого объекта.

1.2.2. Усложненная модель движения тела. Вновь обратимся к задаче нахождения траектории полета камня, выбрасываемого катапультой,

ипродолжим ее исследование. В разд. 1.2.1 мы построили математическую модель движения камня, основанную на четырех упрощающих предположениях, и получили исходную формулу (2.6) для дальности броска. Теперь нам необходимо оценить точность этой формулы и установить пределы ее применимости. Для такого анализа нет нужды строить катапульту по сохранившимся чертежам и проводить соответствующие натурные эксперименты. Это объясняется тем, что по указанному материалу накоплен огромный экспериментальный и теоретический материал, так что нужно только умело воспользоваться им для анализа поставленной задачи.

Предположим, что катапульта может метать камни размером до 0.2 м на расстояние до 100 м, для чего она должна сообщить им начальную скорость порядка 30 м/с. При этом камень поднимется на высоту 20–30 м и пробудет в воздухе около 3 c. В этих условиях первые три предположения выглядят совершенно оправданными, и нам остается только проанализировать справедливость четвертого предположения о влиянии воздуха.

Касаясь вопроса о правомерности этого предположения, отметим,что согласно данным многочисленных опытов на всякое тело, движущееся в воздухе, последний действует с некоторой силой F. Ее модуль F = jFj

инаправление зависят от формы тела и скорости движения. Указанную

силу F можно разложить на две составляющие: параллельную Fr и перпендикулярную F? скорости v. Перпендикулярная составляющая возникает только при асимметрии тела по отношению к направлению движения. Наиболее характерным ее проявлением является подъемная сила, действующая на крыло самолета при его полете, на чем основана вся авиация. Для того чтобы эта сила

могла оторвать самолет от земли и поддерживать его в воздухе, крылу придают специальную форму и располагают его под определенным уг-

лом атаки к набегающему воздушному потоку (см. рис. 2.2). Однако для камня, форма которого близка к сферической, перпендикулярная составляющая F? силы F мала, и ею можно пренебречь (для шара указанная сила в точности равна нулю в силу его симметричности).

13

Параллельная составляющая Fr силы F возникает при движении любого тела. Она направлена в сторону, противоположную движению, и стремится затормозить тело, ее называют силой лобового сопротивления. Таким образом, в рассматриваемом нами случае можно считать, что

Вопрос о конкретном выражении для силы Fr является достаточно сложным и требует привлечения законов аэрогидродинамики. Не имея здесь возможности останавливаться на приведении законов аэрогидродинамики, которые, к слову сказать, также выводятся путем математического моделирования процессов движения тел в сплошных жидких или газообразных средах (см. об этом в § 1.5), отметим, что указанную формулу можно записать в следующем виде:

Здесь v = jvj – модуль скорости v, а a1; a2; : : : – коэффициенты, которые зависят от ряда факторов: формы камня, параметров воздуха и т. д. Часто вместо формулы (2.8) пользуются более простой формулой [55, с. 16]:

где S – площадь поперечного сечения тела, – плотность воздуха, C – безразмерный множитель, называемый коэффициентом лобового сопротивления. Указанный коэффициент зависит от формы тела и безразмерной характеристики Re процесса обтекания, называемой числом Рейнольдса: C = C(Re), Re = v d= . Здесь d – характерный размер тела, и – плотность и вязкость воздуха. Нетрудно проверить, что Re – безразмерная величина, но на этом мы не будем останавливаться.

Оценивая величину Re в интересующем нас случае, когда = 1:3 кг/м3,= 1:7 10 5 кг/(м c), v = 30 м/c, d = 0:2 м, имеем

Эксперименты и теоретические исследования показывают, что для шара в широком диапазоне 3 105 Re 7 106 изменения числа Рейнольдса, содержащем значение Re из (2.10), коэффициент C очень слабо зависит от Re, и его можно считать постоянным и равным 0:15: C 0:15.

Предполагая, что форма камня близка к форме шара радиуса R, и полагая в (2.9) S = R2, приходим к следующей простой формуле для модуля лобового сопротивления шара в указанном диапазоне изменения числа Re:

14

Из этой формулы, в частности, вытекает, что зависимость силы лобового сопротивления от скорости носит квадратичный характер.

Для того чтобы оценить влияние сопротивления воздуха на характер движения камня, сравним его с основной силой в рассматриваемой задаче

– силой тяжести P , действующей вертикально вниз. В случае, когда форма камня является сферической, сила P определяется формулой P = mg = (4 =3)R3 0g. Здесь 0 = 2:3 103 кг/м3 – плотность камня. Заменим в (2.11) v2 на lg (приближенно) и составим отношение Fr=P . Получим:

Fr C R2 lg=2 = 3 C l :

P 4 R3 0g=3 8 0R

При l = 100 м, R = 0; 1 м и C 0:15 получаем Fr=P 0:03.

Обозначим через l абсолютную погрешность, которую мы допускаем в определении дальности броска l, если пренебречь сопротивлением воздуха. При малом сопротивлении воздуха (Fr=P << 1) относительную погрешность l=l можно считать пропорциональной Fr=P с коэффициентом пропорциональности порядка единицы, т. е. в рассматриваемом диапазоне изменения параметров задачи получаем l=l 3% и, следовательно,l = (2 3) м. Если не требуется высокой точности, то такая ошибка допустима, так что применение модели, полученной при выполнении условий 1)–4), оправдано. В противном случае ее следует заменить более сложной моделью, учитывающей трение воздуха.

1.2.3. Дифференциальные уравнения небесной механики. Законы Кеплера как следствие закона тяготения Ньютона. В рассмотренной в п. 1.2.1 задаче векторное дифференциальное уравнение движения можно было разделить на отдельные скалярные уравнения. Таким образом, каждая координата удовлетворяла своему отдельному дифференциальному уравнению, решив которое мы определили эту координату как функцию времени. Теперь же поставим и решим задачу другого типа, когда систему уравнений движения уже не удается разбить простым путем на отдельные уравнения для каждой из искомых функций, и интегрирование такой системы требует более сложных вычислений. В качестве указанной задачи рассмотрим актуальную для человечества задачу определения траектории (или, как говорят астрономы, орбиты) движения планеты вокруг Солнца. Данную задачу будем рассматривать при следующих предположениях:

1)Солнце имеет вид материальной точки массы , расположенной в начале декартовой системы координат;

2)движущаяся планета моделируется материальной точкой массы m, которая в момент t = 0 занимает положение r0 с r0 = jr0j > 0, имея начальную скорость v0;

15

3) тело массой притягивает материальную точку массой m с силой f,

Здесь – гравитационная постоянная (см. ее значение в § 1.3), r = xi + yj + zk – положение точки (планеты) в момент времени t, где i; j и k –

p

единичные орты декартовой системы координат в R3, r = x2 + y2 + z2. В механике указанная сила называется центральной. В результате мы пришли к хорошо известной в механике задаче нахождения движения материальной точки (планеты) массой m под действием центрального силового поля (2.12). Для решения этой задачи опять выберем в качестве основной математической модели второй закон Ньютона (2.1), который с учетом

(2.12) перепишем в виде:

Подчеркнем, что в отличие от (2.3) система (2.14) состоит из трех нелинейных обыкновенных дифференциальных уравнений второго порядка. Хорошо известно, что нахождение точных решений систем нелинейных уравнений в явном виде возможно только в некоторых исключительных случаях. К счастью, в данной ситуации мы имеем тот исключительный случай, когда это возможно. Но для того, чтобы найти точное решение системы (2.14), придется провести ряд математических выкладок.

Мы начнем с того, что выведем в качестве следствия модели (2.13) дифференциальное уравнение первого порядка, выражающее закон сохранения энергии. Для получения этого уравнения умножим первое уравнение в (2.14) на x, второе – на y, третье уравнение – на z и сложим полученные соотношения. Учитывая соотношения x•x = (1=2)d=dt(x2), xx = (1=2)d=dt(x2)

Здесь C – некоторая константа, определяемая, например, из начальных условий. Левая часть (2.16) представляет собой сумму двух слагаемых:

16

первое слагаемое (1=2)m(x2 +y2 +z2) в точности равно кинетической энергии движущейся точки, второе слагаемое m=r имеет смысл потенциальной энергии. Более подробно о физическом содержании этих понятий можно прочитать, например, в [29]. Равенство (2.16) выражает закон сохранения энергии, а именно: при движении материальной точки в центральном поле сил полная энергия, равная сумме кинетической и потенциальной энергий, остается постоянной.

Кроме (2.16) из уравнений (2.14) можно вывести еще три уравнения 1-го порядка. Они имеют вид:

Здесь C1; C2 и C3 – произвольные константы. Для вывода, например, первого уравнения (2.17) умножим третье уравнение системы (2.14) на y, второе – на z и вычтем одно из другого. Получим yz• zy• = 0, или d=dt(yz zy) = 0 =) yz zy = C1. Не умаляя общности, систему коорди-

нат можно выбрать так, чтобы при t = 0 материальная точка находилась в плоскости xy и чтобы ее начальная скорость лежала в той же плоскости, т. е. чтобы в дополнение к 1)–3) выполнялись условия

4) z(0) = 0; z(0) = 0.

В таком случае будем иметь (yz zy)jt=0 = 0, (zx xz)jt=0 = 0. С учетом этого и (2.17) приходим к соотношениям

Из уравнений (2.18) и предположения 4) вытекает, что процесс движения точки происходит в плоскости z = 0. Действительно, поскольку z(0) = 0, то в силу предположения 2) либо x(0) 6= 0, либо y(0) 6= 0. Пусть, например, x(0) 6= 0. Тогда из равенства zx xz = 0 вытекает, что

Но при t = 0 имеем 0 = zjt=0 = axjt=0 = ax(0) ) a = 0; z = 0. Это означает, что z(t) 0. В результате задача интегрирования уравнений (2.14) свелась

к решению двух обыкновенных дифференциальных уравнений:

Для нахождения решения системы (2.19) введем полярные координаты r и по формулам x = rcos , y = rsin . Легко проверить, что x2 + y2 = r2 + r2 _2, xy yx = r2 _. С учетом этого из (2.19) приходим к следующей системе обыкновенных дифференциальных уравнений для r и :

17

Как уже указывалось, первое уравнение в (2.20) выражает закон сохранения энергии. Выясним смысл второго уравнения. Хорошо известно [24], что выражение (1=2)r2 _ равно производной по времени от площади сектора, описываемого радиус–вектором движущейся точки, т. е. равно скорости изменения площади этого сектора. В таком случае второе уравнение в (2.20) утверждает, что эта скорость постоянна. Этот результат получил название второго закона Кеплера или закона площадей: радиус–вектор планеты, движущейся вокруг Солнца, заметает в равные промежутки времени равные площади.

Если “постоянная площадей” k равна нулю, то _ = 0 и = const. Этот случай отвечает движению материальной точки по прямой, проходящей через начало координат, и ниже не будет рассматриваться.

Займёмся теперь определением геометрической формы орбиты планеты. Для этого будем рассматривать r как функцию от . Из второго уравнения (2.20) выводим, что

_ = rk2 ; r drdt = ddr ddt = rk2 ddr:

Подставляя эти соотношения в первое уравнение (2.20), приходим к следующему дифференциальному уравнению для функции r = r( ), описывающей орбиту планеты при ее движении вокруг Солнца:

()

С учетом этого уравнение (2.21) примет следующий вид:

Оно упростится, если ввести вместо r новую неизвестную функцию u, где

18

Новая искомая функция u удовлетворяет дифференциальному уравнению

Это – обыкновенное дифференциальное уравнение первого порядка с разделяющимися переменными. Оно легко интегрируется, в результате чего получаем

Здесь 0 – константа интегрирования. Ее можно выбрать произвольным образом, так как безразлично, от какого фиксированного радиус–вектора следует отсчитывать угол . Примем 0 = =2, так что значению u = 0 соответствует значение = =2. Тогда, взяв синус от (2.25), имеем с учетом

(2.23), что

sin ( 2 ) = cos = pu" ) u = p"cos )

Из аналитической геометрии известно [43, с. 173], что (2.26) представляет собой полярное уравнение кривой второго порядка, один из фокусов которой находится в начале координат. Полученный результат дает первый закон Кеплера: планеты (и кометы) движутся по коническим сечениям, в одном из фокусов которых находится Солнце.

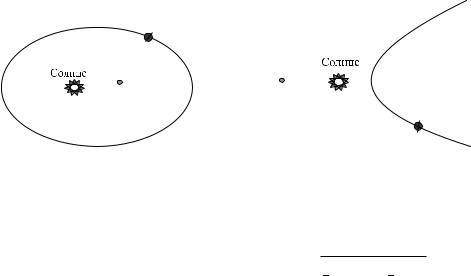
Известно, что существует три типа кривых второго порядка: эллипс, гипербола и парабола. Две возможные в силу первого закона Кеплера ситуации, когда планета движется по эллипсу или по гиперболе, изображены на рис. 2.3,а и 2.3,б. Отметим, что величина p = k2= называется параметром конического сечения, или фокальным параметром; у эллипса и гиперболы параметр p связан с большой и малой полуосями a и b формулой p = b2=a. Величина " > 0, определенная в (2.22), называется эксцентриситетом. Она определяет форму конического сечения, которое является эллипсом при " < 1, параболой при " = 1 и гиперболой при " > 1. Из второго равенства в (2.22) сразу видно, что эти три различные возможности зависят от значений постоянной C, характеризующей энергию: орбита будет эллипсом, если C < 0, параболой, если C = 0, и гиперболой, если

19

Рис. 2.3

где r0 = r(0) – расстояние от точки (планеты) до центра (Солнца) в началь-

p

ный момент времени, а v0 = v(0) = jv(0)j = x2(0) + y2(0). Поскольку C

– абсолютная константа на всем временном интервале, определяющая вид орбиты (являющейся эллипсом, параболой или гиперболой), то из (2.27) следует, что вид орбиты зависит лишь от начального расстояния r0 планеты до Солнца и модуля v0 ее начальной скорости v(0), но не зависит от направления v(0) (при используемом нами предположении, что k 6= 0). В небесной механике показывается, что константа C в (2.27) отрицательна. Отсюда следует очень важный вывод о том, что орбитой Земли является эллипс. Нужно признать, что землянам крупно повезло, поскольку для Земли реализуется именно та благоприятная для существования жизни ситуация, которая изображена на рис. 2.3,а.

Для полного решения задачи осталось определить некоторые количественные характеристики процесса движения планеты и, в частности, период ее обращения вокруг Солнца. Пусть в момент t0 точка занимает положение r0 с координатами (r0; 0), а в момент t > t0 – положение r = (r; ). Интегрируя второе уравнение в (2.20), записанное в виде r2d = kdt, имеем с учетом (2.26), что

Рассмотрим важный для жителей Земли случай, когда орбита имеет вид эллипса (т. е. C < 0). Пусть t таково, что = 0 2 и, следовательно, r = r0. Этому моменту отвечает полное обращение планеты вокруг Солнца, причем величина T = t t0 имеет смысл периода обращения вокруг центра. Поскольку интеграл слева в пределах от 0 до 0 2 дает удвоенную площадь орбитального эллипса [24], равную 2 ab, то из (2.28) приходим к формуле: 2 ab = kT . С другой стороны, постоянная k связана с полуосями a и b соотношением k2= = b2=a = p. Исключив из этих двух равенств k,

20