
s5_atomfiz_exam_nah_book
.pdf
Глава 7. Рівняння Шредінгера
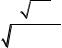
1,2,3 1,2,3сos( 1,2,3x) 1,2,3sin( 1,2,3x), |
(7.12) |
де А і В довільні сталі. Їх можна визначити з таких граничних умов:
1)в областях 1 і 2, де U1,3 , частинка існувати не може, бо не може мати нескінчену енергію, звідки 1,3 і А1,3 = В1,3 = 0;
2)умова неперервності хвильової функції дає
2 0 1 0 ; A2 cos 2 0 B2 sin 2 0 0
a a ; A cos a B sin a 0
2 3 2 2 2 2
Із цих рівнянь знаходимо:
А2 = 0 та 2а n ,
де n - ціле число, яке пробігає значення n = 1, 2, 3,...
Підставимо в (7.13*) 2 із формули (7.11), тоді
E n2 2 2
2m0a2
2 B2 sin( 2x)
(7.13)
(7.13*)
(7.14)
(7.15)
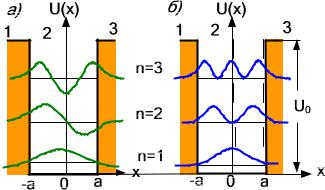
Проаналізуємо отримані результати.
По-перше, енергетичний спектр частинки всередині потенціальної ями дискретний;
По-друге, відсутній рівень із квантовим числом n = 0, бо це супе-
речить співвідношенню невизначеностей. Дійсно, якщо n = 0, то згідно (7.13), Е = 0 і рx = 0, а співвідношення невизначеності дає таке значення для x h px , що вимагає локалізації електрона у всьому просторі, а не в межах бар'єру;
По-третє, інтервал між дискретними рівнями енергії E залежить від ширини потенціальної ями та квантового числа n
E |
|
E |
|
E |
|
2 |
2 |
(2n 1) |
(7.16) |
|
|
||||||||
|
|
n |
|
2m a2 |
|
|
|||
n,n 1 |
n 1 |
|
|
|
|
||||
|
|
|
|
|
|
0 |
|
|
|
У таблиці 7.1 наведені дані для Е при різних а.
Таблиця 7.1. Значення Е при різних а - ширина потенціальної ями
а [Å] |
1 |
10 |
100 |
1000 |
|
|
|
|
|
Е [ерг] |
0,8 10-10 |
0,8 10-12 |
0,8 10-14 |
0,8 10-16 |
Е [еВ] |
0,5 102 |
0,5 |
0,5 10-2 |
0,5 10-4 |
Находкін М.Г., Харченко Н.П., Атомна фізика |
163 |

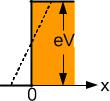









 2
2