s5_atomfiz_exam_nah_book

Глава 6. Хвильова функція електронів

Глава 6. ХВИЛЬОВА ФУНКЦІЯ ЕЛЕКТРОНІВ ТА ЇЇ ФІЗИЧНИЙ ЗМІСТ

«Без участі уяви всі наші відомості про природу обмежилися би класифікацією фактів»

Джон Тіндаль - англійський фізик

6.1. Хвильова функція плоскої хвилі де Бройля. 6.2. Хвильовий пакет, як модель частинки та її недосконалість. 6.3. Фізичний зміст хвильової функції. 6.4. Співвідношення невизначеностей. 6.5. Висновки. 6.6. Контрольні запитання та вправи, тестові завдання. Література.

6.1. Хвильова функція плоскої хвилі де Бройля

Згідно гіпотези Луї де Бройля з частинкою, яка рухається у вільному просторі з постійною швидкістю v, зв’язана плоска хвиля з

Функція називається плоскою хвилею де Бройля з амплітудою 0 і

буде далі показано, в квантовій механіці ці два вирази для фази можна використовувати тому, що фізичний зміст має лише модуль хвильової функції.

Запишемо вираз для фази хвильової функції вільного електрона з урахуванням E i p k h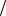 - відомих співвідношень де Бройля (5.23)

Глава 6. Хвильова функція електронів

За допомогою (6.2) проаналізуємо фазову та групову швидкості хвильової функції плоскої хвилі де Бройля.

Фазова швидкість хвилі визначається із умови t - kr = Const

Вона виявляється більшою швидкості світла

Це не дивно, бо фазова швидкість не переносить сигнал, і тому є величиною, що принципово не спостерігається.

Групова швидкість плоскої хвилі де Бройля залежить від дисперсії – залежності k

Групова швидкість плоскої хвилі де Бройля (vгр ) дорівнює v - швидко-

сті частинки (електрона) у вільному просторі. Добуток фазової та групової швидкостей інваріант, бо

v vгр c2v c2 Const . v

6.2. Хвильовий пакет, як модель частинки та її недосконалість

Однією з перших моделей частинки була модель хвильового пакета. Хвильовий пакет - це суперпозиція плоских хвиль де Бройля. Плоскі хвилі лінійні, тому до них можна застосувати принцип суперпозиції. Для спрощення припустимо, що їх амплітуда не залежить від k - хвильового вектора (а f(k)). Тоді хвильовий пакет матиме вигляд:

Глава 6. Хвильова функція електронів

Розвинемо дисперсійне співвідношення хвилі де Бройля1 k) у ряд Тейлора

де введені такі позначення: 0 = k=k0) і 0 = d dk при k = k0. З урахуванням виразу (6.8) формула для фази хвилі де Бройля набуває вигляду

t-kx= 0t+ 0 (k-k0)t-kx+k0x-k0x=( 0t-k0x)+( 0 t-x)(k-k0). (6.9)

Підставивши вираз (6.9) у формулу для хвильового пакета (6.7) і здійснивши інтегрування, отримаємо такий вираз для хвильового пакета:

Проаналізуємо вираз для хвильового пакета (6.11) і знайдемо: його фазову та групову швидкості, просторову локалізацію та протяжність у часі. Фазова швидкість пакета знаходиться із умови сталої фази d/dt ( 0t - xk0) = Const

Вона, як і для плоскої хвилі де Бройля, більша за швидкість світла vфаз = с2/v > c.

Групова швидкість визначається із умови сталої амплітуди па-

кета Const:

1 Дисперсія має місце навіть у вакуумі. Дійсно Е2 = с2р2 + m02c4, тоді

Глава 6. Хвильова функція електронів

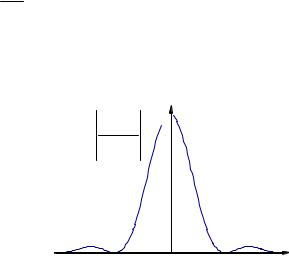
Рис. 6.1. Хвильовий пакет.

тобто групова швидкість збігається зі швидкістю частинки.

Просторова локалізація хвильового пакета характеризується, згідно з (6.11), координатами, при яких його амплітуда В . На рис. 6.1 наведена залежність В2( max2=|sin / |2, де Вmax = 2a k. Видно, що у першому наближенні протяжність пакета можна характеризувати відстанню між двома першими мінімумами - . Зафіксуємо тепер t = Const і знайдемо .

1 2 2 x2 x1 k

Співвідношення (6.15) має місце для довільних лінійних процесів. Во-

но вказує, що для створення локалізованого у просторі пакета з малим інтервалом просторової локалізації x необхідно,

Глава 6. Хвильова функція електронів

щоб p h/ x. Таким чином, чим точніше хвильовий пакет, локалізований у просторі, тим більший набір плоских хвиль де Бройля потрібно використати з різними значеннями імпульсів р або з різними довжинами хвиль де Бройля для того, щоб його утворити.

Щоб знайти протяжність пакета в часі, зафіксуємо коор-

динату точки спостереження x = Const і виберемо два різних значення часу t1 і t2

Виявляється, що чим коротше проміжок часу t між двома послідовними вимірами, тим більша невизначеність енергії.

На перший погляд складається таке враження, що хвильовий пакет із плоских хвиль де Бройля, може бути моделлю матеріальних частинок. Але така точка зору не підтверджується експериментом. Дійсно, коли у виразі для дисперсії k обмежитись не тільки першим членом 0 ряду Тейлора, а використати і другий член ряду

стійкість хвильового пакету суперечить експериментальним фактам. Спробуємо оцінити час розпливання пакета. Для цього в формулі

Якщо у формулі для пакета (6.8) використати вираз (6.18), то під ін-

тегралом з’явиться експонента з показником t k2 2 . Коли цей по-

0

казник стає за порядком величини сумірним з 2 , то лінійне розвинення (6.9) у ряд, що використовується при визначенні sin , втрачає

Глава 6. Хвильова функція електронів

свій зміст. Отже, хвильовий пакет за проміжок часу t 0 розпливається

Оцінимо величини t для різних частинок. Фотон має нульову масу (m0 = 0), тому із (6.5) E = p c, звідки kс, d /dk = c; d2 /dk2 = 0.

Це означає згідно (6.20), що час розпливання фотона t , тобто фотон стійкий, як це й спостерігається експериментально. Для тіла з масою m = 1 г (дробинка) t (10-4)2/(6 10-27) = 1018 c = 109 років, тоб-

то макроскопічні тіла стійкі.

Але елементарні частинки з малою масою спокою та малими розмірами, наприклад, електрони, у яких m0=9,08 10-28 г і x re 10- 12c, мають дуже малий час розпливання t < 9 10-28 ((10-12)2/6) 10-27

= 10-25 c, тобто електрони не стійкі, що суперечить експерименту.

Розглянуті приклади дозволяють дійти висновку, що час розпливання пакета із плоских хвиль де Бройля для елементарних частинок, наприклад електронів, дуже малий, що суперечить експериментальним фактам стабільності частинок. Це примушує відмовитись від моделі частинок у вигляді хвильового пакета.

6.3. Фізичний зміст хвильової функції

Глава 6. Хвильова функція електронів

Дифракційні досліди Бібермана, Сушкина та Фабриканта, а також досліди з інтерференції частинок інших авторів показали, що хвильові властивості частинок притаманні окремим частинкам, а не їх ансамблю. Виявилось також, що кожна частинка взаємодіє зі всією дифракційною ґраткою і в той же час реєструється детектором, як окрема частинка. При повторенні досліду електрон буде зареєстрований іншим детектором. Усе це дає підстави для того, щоб для інтерпретації елементарних взаємодій застосовувати статистичну інте-

рпретацію. Вперше статистичну інтерпретацію хвильової функції запропонував лауреат Нобелівської премії німецький фізик Макс Борн у 1926 році.

БОРН МАКС (1882-1970)

Німецький фізик.

У 1904 поступив до Геттингенського університету, де його професорами були прославлені математики Д.Гільберт, Ф.Клейн та Г.Мінковський. У 1905 став асистентом Гільберта, у 1907 захистив дисертацію, присвячену теорії стійкості пружних тіл. У 1907 Борн відвідував лекції Дж.Дж.Томсона в Кембриджу. Поєднавши ідеї Ейнштейна з математичним підходом Мінковського, створив спрощений метод обчислення маси електрона. У 1915 Борн став асистентом-професором теоретичної фізики М.Планка в Берлінському університеті. У

цей час почалася його багаторічна дружба з Ейнштейном, з яким крім фізики його поєднувала любов до музики – вони складали цілком професійний дует, у якому партію скрипки виконував Ейнштейн, а партію фортепіано – Борн.

У 1919 став професором фізики та директором Інституту теоретичної фізики у Франкфуртському університеті. У 1926 М.Борн зі своїм асистентом В.Гейзенбергом та студентом П.Йорданом розробив математичне обґрунтування квантової механіки, а потім йому вдалося дати статистичну інтерпретацію хвильової функції, введеної Е.Шедінґером. У своїй нобелівській лекції він запитував: „Чи можемо ми дещо, з чим не може асоціювати звичайним чином поняття „положення” та ”рух” називати предметом або частинкою?” і відповідав: „Відповідь на це запитання належить вже не фізиці, а філософії”. Він також розробив метод розв’язування квантомеханічних задач про зіткнення частинок (борнівське наближення), який виявився вкрай важливим для фізики високих енергій; ввів (разом з Н.Вінером) поняття оператора в квантовій механіці. У 1927р розробив (разом із Р.Оппенгеймером) теорію будови двохатомних молекул.

Борн був нагороджений медаллю Макса Планка Німецького фізичного товариства (1948), медаллю Хьюза Лондонського королівського товариства та ін.; він був членом багатьох наукових товариств і академій. Лауреат Нобелівської премії 1954р. з фізики «за фундаментальні дослідження з квантової механіки, особливо за його статистичну інтерпретацію хвильової функції».

Глава 6. Хвильова функція електронів

У 1955р. Борн і ще 15 Нобелівських лауреатів виступили із заявою про відповідальність вчених у зв'язку з дослідженнями в області створення зброї масового знищення, і що засуджують подальшу розробку і використання ядерної зброї.

Він висловив гіпотезу, що хвильова функція є принципово комплексною, яка не спостерігається. Це означає, що фізичний зміст має лише квадрат хвильової функції, яка є густиною ймовірності знайти частинку в даній точці простору.

Коли відома хвильова функція r,t , то ймовірність знайти частинку в елементі об'єму d3r = dxdydz дорівнює

Частинка у вільному від полів просторі є плоскою хвилею де Бройля

вана, а розмазана по всьому вільному простору.

Для хвильових функцій виконується принцип суперпозиції - один із найбільш важливих принципів квантової механіки, який разом із співвідношеннями невизначеності (6.15) і (6.18*) визначає структуру її математичного апарату. Принцип суперпозиції полягає в тому, що коли частинка може знаходитись у стані з хвильовою функцією 1 або в стані з хвильовою функцією 2 , то вона може

також знаходитись ще й в стані, котрий описується лінійною комбінацією цих хвильових функцій

де С1 та С2 - довільні комплексні числа, які визначають долю (внесок) амплітуд та фаз станів 1 і 2, що входять до хвильової функції складного стану , у якому такі ж вимірювання, як і при визначенні фізичних величин у станах 1 і 2 дають у новому стані фізичні вели-

чини станів 1 і 2 із ймовірностями C1 C1 і C2C2 . Необхідність вве-

дення принципу суперпозиції станів обумовлена корпускулярнохвильовим дуалізмом – загальною і універсальною властивістю природи. Він дозволяє усунути протиріччя між хвильовим і корпускулярним описом, що існував у рамках класичних уявлень про частинки як матеріальні точки, які рухаються вздовж певних траєкторій, й

Глава 6. Хвильова функція електронів

описувати їх хвильові властивості в термінах корпускулярних уявлень.

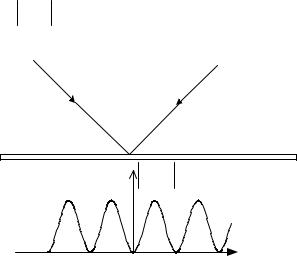
Розглянемо приклад інтерференції дифрагованих електронів на двох щілинах (рис.6.2), як і раніше у розділі 5.4. Нехай для спрощення задачі хвильові функції електронів, що пройшли крізь першу та другу щілини, мають вигляд плоских хвиль де Бройля з різними фазами

1,2 exp{-i( t - kx - 1,2)} , (6.24)

де 1 і 2 - різниця фаз при проходженні електроном першої або другої щілини. За принципом суперпозиції хвильова функція змішаного стану має вигляд

1 2 exp{-i( t - kx)} [exp{i 1)}- exp{i 2)}].

Тоді густина ймовірності знайти електрон у цьому стані це квадрат модуля цієї хвильової функції:

де 2 1 = f(x). Вона залежить від координат точки спостереження х. У площині спостереження утворюється дифракційна картина просторового перерозподілу густини ймовірності у вигляді мінімумів та максимумів 4cos2 x 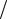2 (рис.6.2), яка якісно збігається

з експериментальним розподілом (рис.5.21).

Рис.6.2. Інтерференція дифрагованих хвиль на двох щілинах.

Глава 6. Хвильова функція електронів

Вираз (2.23) для принципу суперпозиції, подібний до відповідного виразу в класичній фізиці. Проте він має дві істотні відмінно-

сті по відношенню до виразу класичної фізики.

По-перше, на відміну від класичної фізики, у квантовій механіці у стані ми отримуємо при вимірюванні не комбінацію фізичних величин М1 і М2, а тільки одну з величин М1 або М2. Імо-

вірність отримати М1 або М2 після вимірювання визначається коефі-

рактеризується значенням фізичної величини, наприклад, для 1 -

бо не є плоскою хвилею де Бройля з одним значенням імпульсу

p k , а є проміжним станом між станами 1 і 2. Отже квантова механіка допускає проміжні стани між станами 1 і 2, у яких деякі

фізичні величини не мають визначених значень (див. співвідношення (6.15) і (6.16*)). Тобто суть квантово-механічної логіки полягає в тому, що квантова система можливих станів обирає не один із станів „той” або „той”, а всі зразу і „той” і „той”. Цим вона відрізняється від класичної логіки, де використовується вибір „або - або”.

По-друге, в класичній фізиці складання двох станів дає новий стан, наприклад, нове коливання, а в квантовій механіці складання двох однакових станів зводиться до множення хвильової функції на сталий множник, тобто ми отримуємо той же самий стан. Фі-

зичні величини при квантовій суперпозиції не змінюють своїх значень, бо не змінюють свого стану.

Таким чином, принцип суперпозиції показує, що із квантових станів, котрі є в нашому розпорядженні, можна багатьма способами створювати нові стани і кожний стан можна розглядати як результат суперпозиції двох або багатьох інших станів, причому це можна здійснювати нескінченною кількістю способів. Тобто будь-яка хвильова функція може бути розкладена на суму (взагалі нескінчену) власних функцій оператора будь-якої фізичної величини М, наприклад енергії, імпульсу, моменту

імпульсу тощо, при цьому квадрат модулів коефіцієнтів Ci Ci у ро-

зкладі мають зміст ймовірностей для величини М набувати значення Мі.