8.3 Модели принятия решений

Принятие решений – основная часть работы менеджеров любого звена любого предприятия. Поэтому понимание всех тонкостей процесса принятия решений в различных условиях, знание и применение различных методов и моделей принятия решений играет значительную роль в повышении эффективности работы управленческого персонала.

Решение принимается в условиях определенности, когда руководитель может с точностью определить результат каждого альтернативного решения, возможного в данной ситуации. Сравнительно мало организационных или персональных решений принимается в условиях определенности.

Решение принимается в условиях неопределенности, когда невозможно оценить вероятность потенциальных результатов. Это имеет место, когда требующие учета факторы настолько новы и сложны, что невозможно получить достаточно релевантной информации, могущей помочь объективно определить вероятность, либо имеющаяся ситуация не подчиняется известным закономерностям. Поэтому вероятность определенного последствия невозможно предсказать с достаточной степенью достоверности. Неопределенность характерна для некоторых решений, принимаемых в быстро меняющихся условиях. К таким решениям относятся решения по поводу прогнозирования, как результатов хозяйственной деятельности предприятия, так и отдельных аспектов его функционирования.

Моделирование широко используется для принятия решений. Модель – это представление объекта, системы или процесса в форме отличной от оригинала, но сохраняющей основные его характеристики. Причинами, обуславливающими применение моделирования в экономике, являются: естественная сложность многих организационных ситуаций, невозможность проведения экспериментов в реальной жизни и ориентация руководства на будущее.

В науке управления используются следующие модели: - теория игр; - модели теории очередей;

- модели управления запасами; - модель линейного программирования; - транспортные задачи; - имитационное моделирование; - сетевой анализ; - экономическийанализ.

При принятии решения вне зависимости от применяемых моделей существуют некоторые правила принятия решений. Правило принятия решения – это критерий, по которому выносится суждение об оптимальности данного конкретного исхода. Существует два типа правил. Один не использует численные значения вероятных исходов, второй – использует данные значения.

К первому типу относятся следующие правила принятия решений:

47

1.Максимаксное решение – это решение, при котором принимается решение по максимизации максимально возможных доходов. Данный метод очень оптимистичен, то есть не учитывает возможные потери и, следовательно, самый рискованный.

2.Максиминное решение – это решение, при котором максимизируется минимально возможный доход. Данный метод в большей степени учитывает отрицательные моменты различных исходов и является более осторожным подходом к принятию решений.

3.Минимаксное решение – это решение, при котором минимизируются максимальные потери. Это наиболее осторожный подход к принятию решений и наиболее учитывающий все возможные риски. Под потерями здесь учитываются не только реальные потери, но и упущенные возможности.

4.Критерий Гурвича. Данный критерий является компромиссом между максиминным и максимаксным решениями и является одним из самых оптимальных.

Ко второму типу принятия решений относятся решения, при которых кроме самих возможных доходов и потерь учитываются вероятности возникновения каждого исхода. К данному типу принятия решений относятся, например, правило максимальной вероятности и правило оптимизации математического ожидания. При данных методах обычно составляется таблица доходов, в которой указываются все возможные варианты доходов и вероятности их наступления. При использовании правила максимальной вероятности соответственно выбирается по одному из правил первого типа один из исходов, имеющий максимальную вероятность.

При использовании правила оптимизации математических ожиданий, высчитываются математические ожидания для доходов или потерь и затем выбирается оптимальный вариант.

Так как значения вероятностей со временем изменяются, при применении правил второго типа обычно используется проверка правил на чувствительность к изменениям вероятностей исходов.

Кроме того, для определения отношения к риску используется понятие полезности. То есть для каждого возможного исхода кроме вероятности рассчитывается полезность данного исхода, которая также учитывается при принятии решений.

Прогнозирование – метод, в котором используется как накопленный в прошлом опыт, так и текущие допущения насчет будущего с целью его определения. Результат качественного прогнозирования может служить основой планирования. Существуют различные разновидности прогнозов: экономические прогнозы, прогнозы развития технологии, прогнозы развития конкуренции, прогнозы на основе опросов и исследований, социальное прогнозирование.

Таким образом, принятие решений – связующий процесс, необходимый для выполнения любой управленческой функции. В условиях рыночной экономики менеджер своими решениями может повлиять на судьбы многих людей и организаций.

В зависимости от уровня сложности задач, среда принятия решений варьируется

взависимости от степени риска. Условия определенности существуют, когда руководитель точно знает результат, который будет иметь каждый выбор. В условиях риска вероятность результата каждого решения можно определить с известной достоверностью. Если информации недостаточно для прогнозирования уровня вероятности результатов в зависимости от выбора, условия принятия решения являются неопределенными. В условиях неопределенности руководитель на основе собственного суждения должен установить вероятность возможных последствий.

Модели принятия решений основываются па теории игр. Они применяются в условиях неопределенности или ситуациях, когда интересы сторон не совпадают.

48

Каждая из сторон принимает такие решения, т.е. выбирает такую стратегию действий, которая с их точки зрения обеспечивает наибольший выигрыш или наименьший проигрыш. Причем каждой из сторон ясно, что результат зависит in только от своих действий, но и от действий партнеров. Например, противоборство конкурентов в процессе борьбы за рынок сбыта конкретного вида продукции.

Теория игр впервые была систематически изложена Дж.фон Нейманом и О.Моргенштерном в 1944 г., хотя отдельные результаты были опубликованы еще в 20-х годах. Нейман и Моргенштерн написали оригинальную книгу, которая содержала главным образом экономические примеры, поскольку экономическому конфликту легче всего придать численную форму. Во время второй мировой войны и сразу после нее теорией игр серьезно заинтересовались военные, которые увидели в ней аппарат для исследования стратегических решений. Затем главное внимание, снова стало уделяться экономическим проблемам. Сейчас ведется большая работа, направленная на расширение сферы применения теории игр.

Теория игр занимается изучением т.н. конфликтных ситуаций, где сталкиваются интересы индивидов, партий, государств и т. п.

Как утверждал Г.Лейбниц, "...и игры заслуживают изучения; и если какой-нибудь проницательный математик посвятит себя их изучению, то получит много важных результатов, ибо нигде человек не показывает столько изобретательности, как в игре ".

Нет математической теории, которая могла бы дать алгоритм любой реальной игры, но существуют ситуации, подобные игровым и допускающие математический анализ.

Остановимся на классификации игр.

Интересы участников игры (игроков) могут оказаться несовпадающими и даже противоположными. В последнем случае игра называется антагонистической.

В игре могут участвовать два или более игроков. Случай игры с одним участником (пасьянс, управление физическим объектом и т.д.) в сущности является игрой двух лиц, где вторым участником выступает природа (судьба, рок, провидение).

Игроки могут в игре выступать каждый за себя или объединяться в группы. В последнем случае игра называется коалиционной.

Игры, в которых игроки осведомлены о состоянии своем и партнеров, а также о прошлом поведении участников игры, относятся к категории игр с полной информацией (типичные примеры - шахматы, "крестики-нолики" и т.п.). Большинство же игр протекает в условиях неполной информации, где сведения о состоянии партнеров исчерпываются лишь вероятностными характеристиками (домино, карточные игры, игры против "природы").

Антагонистическую игру, где выигрыш одного коллектива равен проигрышу другого, называют игрой с нулевой суммой.

Система правил, однозначно определяющая выбор хода игрока в зависимости от сложившейся ситуации, называется стратегией.

Каждая фиксированная стратегия игрока, где любой ситуации сопоставлен конкретный выбор, называется чистой. В реальности чаще используются т.н. смешанные стратегии, где чистые стратегии смешиваются с некоторыми частотами.

Простейшими являются игры 2 лиц с нулевой суммой.

Пусть в такой игре игрок 1 имеет m выборов и игрок 2 - n выборов. Если игрок 1 делает свой i-й выбор, а игрок 2 - свой j-й выбор, то выигрыш игрока 1 (проигрыш игрока 2) равен Rij. Такая игра называется матричной и матрица R = [ Rij / i=1..m , j=1..n ] называется матрицей выигрышей (платежной матрицей).

49

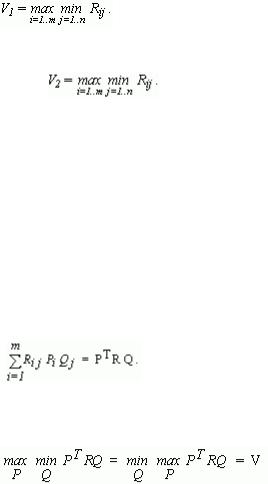
При ведении игры игрок должен ориентироваться на оптимальную политику партнера и наказывать его за отступления от таковой.

Проведем рассуждения за игрока 1. Если Я воспользуюсь i-м выбором, мой противник для минимизации моего выигрыша сделает тот из своих выборов, который даст min Rij. Соответственно, Я должен использовать тот выбор, который гарантирует мне выигрыш, не меньший

(1)

Противник, рассуждая аналогично, приходит к выводу о гарантированном проигрыше, не превышающем

(2)

Если в матрице выигрышей существует элемент Rkl = V1 = V2, то говорят о наличии оптимальной политики "в пространстве чистых стратегий" и оптимальными выборами для игроков соответственно являются выборы k и l. Пару (k, l) называют седловой точкой.

При анализе игр часто прибегают к попыткам обнаружить доминирование между строками и столбцами. Использование доминирования т.о. позволяет уменьшить размеры изучаемой матрицы исключением "невыгодных" строк и столбцов. При отсутствии седловой точки среди чистых стратегий приходится искать таковую среди смешанных.

Если игрок 1 прибегает к своему выбору i с вероятностью Pi, а игрок 2 - к своему j-му выбору с вероятностью Qj, то ожидаемый выигрыш игрока 1 (проигрыш игрока 2) равен

(3)

Основная теорема теории игр (теорема Джона фон Неймана) утверждает, что любая матричная игра с нулевой суммой всегда имеет седловую точку, т.е. существуют векторы P и Q такие, что

(4)

(V - цена игры).

8.4 Имитационное моделирование

Имитация — это попытка дублировать особенности, внешний вид и характеристики реальной системы. Идея имитации реализуется следующим образом:

-математическое описание реальной ситуации;

-изучение ее свойств и особенностей;

-формирование выводов и принятие решений, связанных с воздействием на эту ситуацию и основанных на результатах имитации.

Важно, что реальная система не подвергается воздействию до тех пор, пока преимущества или недостатки тех или иных управленческих решений не будут оценены

спомощью модели этой системы.

Метод Монте-Карло (метод статистических испытаний) состоит из четырех этапов.

1 Построение математической модели системы, описывающей зависимость моделируемых характеристик от значений стохастических переменных.

2 Установление распределения вероятностей для стохастических переменных.

3 Установление интервала случайных чисел для каждой стохастической

50

переменной и генерация случайных чисел.

4 Имитация поведения системы путем проведения многих испытаний и получение оценки моделируемой характеристики системы при фиксированных значениях параметров управления. Оценка точности результата.

Описание этапов:

Первый этап. Стохастическая имитационная модель (ИМ) некоторой реальной системы может быть представлена как динамическая система, которая под воздействием внешних случайных входных сигналов (входных переменных) изменяет свое состояние (случайные переменные состояния), что, в свою очередь, приводит к изменению выходных сигналов (выходных переменных):

где F, R — векторы-функции;

Ii, Ui, Si — векторы входных, выходных переменных и переменных состояния системы в тактовый момент моделирования i соответственно.

Имитационная модель — это экспериментальная модель системы, в которой искусственно воспроизводятся случайности, имеющие место в реальной системе. Она представляет собой совокупность математических соотношений между входными, выходными переменными и переменными состояния в сочетании с алгоритмической реализацией некоторых зависимостей.

Существует два подхода в имитационном моделировании динамических процессов.

Первый заключается в том, что весь период моделирования разбивается на равные промежутки времени (такты моделирования) и анализ состояния системы, а также значений выходных переменных производится через одинаковые промежутки времени. При таком подходе возникает проблема выбора «правильной» продолжительности такта. Кроме того, не исключается появление тактов, в которых состояние системы по сравнению с предыдущим не изменилось.

При втором подходе величина такта моделирования не фиксируется, моделирование в этом случае происходит в момент наступления одного из «существенных» событий. Например, при моделировании производственного процесса на предприятии такими событиями могут быть освобождение или начало загрузки станка, поступление на обработку детали, невыход на работу станочника, исчерпание запаса необходимых комплектующих деталей на складе и др. Именно второй подход чаще всего используется на практике и поддерживается современными языками моделирования.

Второй этап. Случайные величины, используемые в ИМ, могут быть дискретными или непрерывными. В первом случае необходимо знать их распределения, во втором — плотности распределений. Эти зависимости могут быть известны из теории, определены в результате специальных исследований либо заданы в качестве гипотезы. Точность модели (при прочих равных условиях) зависит от того, насколько точно заданы указанные распределения (плотности распределений).

Третий этап. Моделирование случайных величин при компьютерных имитационных экспериментах производится с помощью датчика псевдослучайных чисел, предусмотренного в любом современном языке программирования. Обычно это датчик случайных чисел с равномерным распределением на интервале [0, 1]. Если известны вероятности наступления событий, то, используя такой датчик, можно

51

отвечать на вопросы: «Какое из N возможных событий произошло?» или «Какое значение приняла случайная величина?»

Предположим, что в ИМ используется случайная величина X, принимающая

N

дискретные значения х1, х2,..., хN с вероятностями соответственно p1, p2,..., pn (∑pk =1) .

k =1

Получение некоторой реализации этой переменной в модели производится следующим образом.

Строится функция распределения случайной величины X. Указанная функция

определяется посредством равенства F(X) = ∑pk, в котором суммирование распространяется на все индексы, для которых хk < X. С помощью датчика случайных чисел получают случайное число и из отрезка [0, 1].

Из равномерности распределения получаемых случайных чисел следует, что вероятность получения случайного числа из произвольного интервала, включенного в [0, 1], равна длине этого интервала. Поэтому вероятность реализации Х = х k равна вероятности попадания полученного от датчика случайного числа и в произвольный интервал длиной pk на отрезке [0, 1]. Таким образом, можно утверждать, что если очередное число и датчика удовлетворяет неравенствам 0 < и ≤ р1, то имеет место реализация Х = х1, в случае p1 < и ≤ p1 + р2 — реализация Х = х2 и т. д. В общем случае

Заметим, что границы указанных неравенств совпадают со значениями построенной выше функции распределения F(X).

Однако, удобнее работать не с дробными значениями границ интервалов, в которые попадает случайное число и, а с их целочисленными значениями, тем более, что

спомощью датчиков случайных чисел можно генерировать числа из любого диапазона. Чтобы получить целые значения границ интервалов, достаточно умножить все pk на 10d, где d — целое, минимальное значение которого равно максимальной точности

(максимальному числу знаков после десятичной точки) чисел pk, k = 1,..., N. Например, если {рk} = {0,3; 0,153; 0,5; 0,047}, то минимальное значение d равно 3 (все рk нужно умножить на 1000). Таким образом, 10d определяет длину интервала значений рассматриваемой случайной величины в ИМ.

Четвертый этап. Точность статистических оценок параметров реальной системы зависит от числа наблюдений (объема выборки). Погрешности в оценках обусловлены как статистическим характером самой модели, так и влиянием начальных данных (начального состояния имитационной системы), а также возможной автокорреляцией последовательных значений некоторого параметра в процессе моделирования. Очевидно, что с увеличением числа испытаний точность моделирования должна возрастать. Ввиду того что увеличение объема выборки связано

сростом затрат на моделирование, важно уметь определять минимальное число испытаний, необходимое для достижения заданной точности оценки с заданной вероятностью.

Широкое распространение получили два метода статистических испытаний. Один из них предполагает проведение достаточно большого числа Т последовательных наблюдений в течение одного прогона модели (одного сеанса имитирования).

Другой метод заключается в реализации т независимых прогонов модели, т.е. в m-кратном повторении одного и того же цикла имитирования. При этом, если необходимо получить в сумме Т наблюдений, в течение каждого прогона можно делать по Т/т (допустим, что это число целое) наблюдений. Оба метода дают примерно одинаковый результат.

52

Пусть значения уt (t = 1,..., Т) представляют собой результаты Т последовательных измерений значений случайной величины y во время одного и того же сеанса имитации. Среднее по времени значение у определяется выражением:

t=1

Обозначим через µ математическое ожидание случайной величины у. Тогда для достаточно большого T получаем:

Оценка дисперсии y (если временной ряд не является автокоррелированным) имеет вид:

где D(у) — дисперсия случайной величины у.

Для оценки качества результатов, полученных методом Монте-Карло при неизвестной дисперсии наблюдаемой случайной величины, предположим, что Z - характеристика, которая должна быть определена (вероятность события,

математическое ожидание, дисперсия и т.п.), a ξ - ее значение, уточняемое по мере накопления данных, остающееся случайным вследствие ограниченности числа T проведенных наблюдений. В этих условиях можно говорить о вероятности p(|Z – ξ| < ε) по отношению к интересующей нас характеристике. Величина |Z – ε | представляет собой погрешность в оценке Z, a ε - некоторый допустимый ее предел.

Из неравенства Чебышёва следует, что

Из неравенства (4.6) следует:

откуда при заданных р и ε и при известной зависимости Dξ(Т) можно найти предельно необходимое Т.

Известно, что истинная дисперсия выборочного распределения для расчетного среднего обратно пропорциональна суммарному числу наблюдений Т:

где d не зависит от Т.

В начале имитационного процесса требуемое число наблюдений определить обычно не удается, поскольку d неизвестно. Поэтому, как правило, эксперимент проводят в два этапа.

На первом этапе число испытаний выбирается относительно небольшим, в результате определяется величина d. После этого уже можно определить, сколько дополнительных наблюдений необходимо, чтобы была достигнута требуемая точность.

Предельное число наблюдений Т0 определяется формулой

53