
Контрольная по ВМатем
.pdf
1 |
y ' = − sin x ln sin x + cos x |
1 |
cos x |
|
y |
sin x |
|||
|
|
|
|
cos |
2 |
x |
|
y ' = y |
− sin x ln sin x + |
|
|
||
|
|
|
|||
|
|
sin x |
|||
y ' = (sin x ) |
cos x |
− sin x ln sin x + |
cos2 x |
|
|
|
|
||
|
||||
|
|
|
sin x |
|
г) Дифференцируя обе части равенства, имеем
y= 1 + xe y
y' = e y + xe y y '
y'(1 − xe y ) = e y
y ' =
e y
1 − xe y
Т.к. по условию xe y = y −1 , то получаем
y ' = |
e y |
|
= |
e y |
|
|
|
|
1 − y +1 |
2 − y |
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
|
1 |
|
|
Задача 12. Дана функция f ( x) = 5 |
2− x в точке x |
= 0 и x = 2 |
||||||
|
|
|
|
|
|
1 |
2 |
|
а) Установить является ли функция непрерывной в этих точках б) Найти пределы слева и справа в) Сделать схематический чертеж
Решение:
В точке x = 0 функция непрерывна, т.е.
1 |
|
1 |
|||
|
|
|
|
|
|
lim 52− x = f (0) = |
5 = lim 52− x |
||||
x→0−ε |
|
x→0+ε |
|||
В точке x = 2 |
|
|
|
||
21
предел слева
1 1
lim
lim 52− x = 5x→2−ε 2− x = 5+∞ = ∞
x →2−ε
предел справа
1 1
lim
lim 52− x = 5x→2+ε 2− x = 5−∞ = 0
x→2+ε
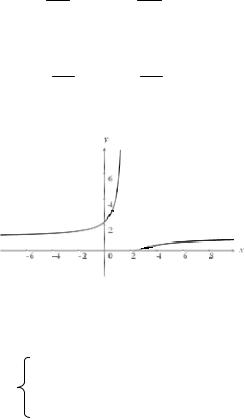
Схематичный чертеж на рис 1
Рисунок 1
Задача 13.
x + 1, если x ≤ 0
Дана функция y = x2, если 0 > x ≤ 2 ½ x + 3 , если x ≥ 2
Найти точки разрыва, если они существуют сделать чертеж.
Решение:
График функции изображен на рисунке
22
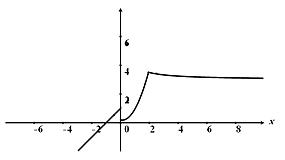
В точке x = 0 |
разрыв первого рода т.к. lim f (x) = 1 |
|
|
|
x→0−ε |
lim f (x) = 0 |
|
|
x→0+ε |
|
|
В точке x = 2 |
разрыва нет. lim |
f ( x) = lim f ( x) = 4 |
|
x→ x +ε |
x→ x −ε |
В остальных точках функция непрерывна.
Задача 14.
a) С помощью преобразования графика функции y = sin x построить функцию y = −2 sin(2x + 2)
Решение:
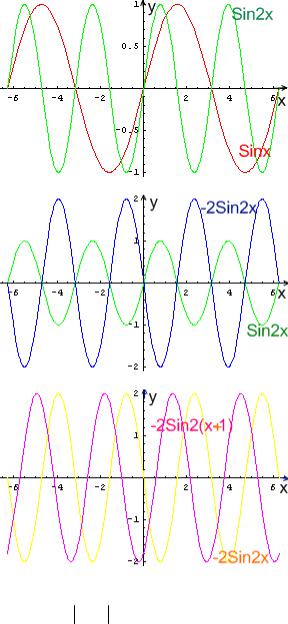
От функции y = sin x к функции y = −2 sin(2x + 2) можно перейти с помощью следующей цепочки преобразований: y = sin x
y = sin 2x y = −2 sin 2x y = −2 sin 2( x + 1)
На рисунке изображены соответствующие графики:
23
б) Построить по точкам график функции y = −x2 + x − 2 +1
24

Решение:
Рассмотрим два случая
1) x – 2 ≥ 0 |
x ≥ 2 |
тогда |
y = −x2 + x −1 |
2) x – 2 < 0 |
x < 2 |
тогда |
y = − x2 − x + 3 строим график |
Задача 15. Используя правило Лопиталя вычислить пределы:
а) lim |
e3 x |
− 3x −1 0 |
|
|
|
|
|
|
|||||||||
sin |
2 |
5x |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||||||
x→0 |
|
|
0 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
(e3x −3x −1)' |
|
|
|
|
3e3x −3 |
|
0 |
|
|
|||||||
lim |
|
|
|
|
|
|
= lim |
|
|
|
= |
|
|
|
= |
||
|
|
|
|
|
|
|
|
|
|
|
|||||||
x→0 (sin2 |
5x)' |
|
x→0 2sin5x cos5x 5 |
|
0 |
|
|
||||||||||
= lim |
(3e3x −3)' |
= lim |
9e3x |
|
|
= |
9 |
|
|
|||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||
x→0 (5sin10x) ' |
x→0 50 cos10x 50 |
|||||||||||
lim x 2 ln x = lim |
|
ln x |
= |
|
−∞ |
= |
||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|||||||||
x → 0 |
x → 0 1 x 2 |
|
|
∞ |
|
|
||||||
б) |
(ln x ) ' |
|
1 x |
|
1 |
|
|
= lim |
= lim |
= − |
lim x 2 = 0 |
||||
|
|
|
|||||
x → 0 (1 x 2 ) ' |
x → 0 −2 x 3 |
|
2 x → 0 |
||||
25
|
|
|
|
|
|
1 |
|
|
|
|
|
cos x |
|
|
1 |
|
|
|
|
|
|
|||||||
|
lim ctgx − |
|
|
= lim |
|
|
|
|
|
|
− |
|
|
|
= |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
x→0 |
|
|
|
|
x |
|
|
|
x→0 |
sin x |
|
|
|
x |
|
|
|
|
|
|
|||||||
в) |
|
|
x cos x − sin x |
|
|
|
0 |
|
|
|
|
|
(x cos x − sin x) ' |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
= lim |
|
|
|
|
|
|
|
|
= |
|
|
= lim |
|
|
|
|
= |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
x→0 |
x sin x |
|
|
|
|
|
|
0 |
|
|
x→0 |
|
(x sin x) ' |
|
|
||||||||||||
= lim |
|
cos x − x sin x − cos x |
= lim |
|
−x sin x |
= |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
x→0 |
|
|
|
sin x + x cos x |
|
|
|
|
|
|
x→0 sin x + x cos x |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−x2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= |
sin x ~ x при x → 0 |
= lim |
|
|
|
|
|
|
= |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
−x |
|
|
|
0 |
|
|
|
|
x→0 x + x cos x |
|
|
||||||||||||
= lim |
|
|
|
|
|
= |
= 0 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 |
+ cos x |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
г) lim (ex + x )1 x
x→0
Имеем неопределённость вида 1∞ . Положим y = (ex + x )1 x и
прологарифмируем обе части равенства
ln y = 1x ln(ex + x)
Найдём
lim ln y = lim |
ln(ex |
+ x) |
= |
|
0 |
|
|
= |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
x |
|
|
|
|
|
||||||||||
x→0 |
x→0 |
|
|
|
|
|
0 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
ex |
+ 1 |
|
|
|
|
|||
|
(ln(ex + x)) ' |
|
|
|
|
|
|
|||||||||
= lim |
= lim |
ex |
+ x |
= |
1 + 1 |
= 2 |
||||||||||
|
|
|
|
|||||||||||||
x→0 |
x ' |
|
|
x→0 |
|
|
1 |
|
|
1 + 0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Поскольку |
|
lim ln y = 2 , то |
|
|
|
lim y = lim(ex + x)1 x = e2 |
||||||||||
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
x→0 |
x→0 |
|
26

Задача 16. Исследовать методами дифференциального исчисления функцию и, используя результаты исследования, построить её гра-
фик: y =
x3
2( x + 1)2
Решение: Приведём схему полного исследования функции
1.Область определения функции
2.Чётность, нечётность, переодичность
3.Точки разрыва функции; приделы при x → k концам промежутков области определения; асимптоты
4.Интервалы возрастания и убывания функции, точки экстремума; вычислить значения экстремумов
5.Интервалы выпуклости и точки перегиба
6.Точки пересечения графика с осями координат
7.График
1. Функция f (x) определена, если |
x + 1 ≠ 0 |
, значит |
|
|
x ≠ −1 |
D( y) = (−∞; −1) (−1; +∞) |
|
2. Т.к. область определения функции D( y) не является симмет-
ричным множеством относительно начала координат, то функция f (x) не может быть чётной, нечётной и периодической.
3. Найдём пределы функций при x → k концам промежутков области определения
|
|
x3 |
|
∞ |
|
( x3 ) ' |
|
|
lim |
f (x) = lim |
|
= |
|
|
= lim |
|
= |
|
|
|
||||||
x→−∞ |
x→−∞ 2(x + 1)2 |
|
∞ |
x→−∞ (2( x + 1)2 ) ' |
|
|||
|
3x2 |
|
∞ |
|
6x |
|
|
= lim |
|
= |
|
|
= lim |
|
= −∞ |
|
|
|
|||||
x→−∞ 2(x + 1) |
|
∞ |
x→−∞ 4 |
|
|||
27

x3
Аналогично, получаем что lim = +∞
x→+∞ 2(x + 1)2
Поскольку
lim |
|
|
x3 |
|
= −∞ , то точка x = −1 - точка разрыва второго |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
x→−1 2(x + 1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
рода, а x = −1 - вертикальная асимптота. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Найдём наклонные асимптоты y = kx + b , где |
|
|
|
|||||||||||||||||||||||||||||||||
k = lim |
|
f ( x) |
|
= lim |
|
|
|
|
|
x3 |
|
|
|
|
= lim |
|
|
x2 |
|
= |
1 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
x→∞ |
x |
|
|
|
x→∞ 2x(x + 1)2 |
|
x→∞ 2( x + 1)2 |
|
2 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
3 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
b = lim( y − kx) = lim |
|
|
|
|
|
|
|
− |
x |
= |
|
|
|
|
||||||||||||||||||||||
|
2( x + 1)2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
x→∞ |
|
|
|
|
|
x→∞ |
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
x3 |
− x( x + 1)2 |
|
|
|
−2x2 − x |
|
|
−2 |
|
|
|
|
||||||||||||||||||||
= lim |
|
|
|
|
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
= |
|
|
= −1 |
|
|
|||||||||
|
2( x + 1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
x→∞ |
|
|
|
|
x→∞ 2( x + 1)2 |
|
|
2 |
|
|
|
|
|
||||||||||||||||||||||
Следовательно, y = |
x |
− 1 - уравнение наклонной асимптоты |
||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4. Производная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
y ' = |
|
3x2 |
2( x + 1)2 − x3 4( x + 1) |
= |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
4(x + 1)4 |
|
|
|
|
|
|
|
|
|
определена на D( y) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
2x3 + 6x2 |
|
|
|
|
2x2 |
(x + 3) |
|
|
|
|
x2 ( x + 3) |
||||||||||||||||||||||||
= |
= |
|
= |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
4( x + 1)3 |
|
4(x + 1)3 |
|
2(x + 1)3 |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Поскольку y ' = 0 при x = −3 , |
|
x = 0 , то это критические точки |
||||||||||||||||||||||||||||||||||
функции. Так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
28

|
|
x2 |
(x + 3) |
x < −3 |
|
y ' > 0 |
при |
> 0 −1 < x < 0 |
|||
2(x + 1)3 |
|||||
|
|
|
|||
|
|
|
|
0 < x < 1 |
|
y ' < 0 |
при |
x2 |
(x + 3) |
< 0 −3 < x < −1 |
|
|
|
||||
2(x + 1)3 |
|||||
|
|
|
|||
то на интервалах (−∞; −3) , (−1;0), (0; +∞) функция возрастает, а
на интервале (−3; −1) - убывает.
При x = −3 функция имеет максимум, т.к. переходе через эту точку y ' меняет знак с «+» на « − ».
f (−3) = − |
27 |
|
|
|
−3; − |
27 |
|
|
|
|
||
|
, значит точка |
|
- точка максимума. |
|||||||||
|
|
|||||||||||
|
|
|
8 |
|
|
|
|
8 |
|
|
|
|
5. Находим вторую производную |
|
|
|
|
|
|||||||
y " = |
x3 + 3x2 |
' |
= |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||||
|
2( x + 1)3 |
|
|
|
|
|
|
|
|
|||
= |
(3x2 + 6x) 2(x + 1)3 − ( x3 |
+ 3x2 ) 6( x + 1)2 |
= |
3x |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
4( x + 1)6 |
|
|
|
( x + 1)4 |
|||
|
|
|
|
|
|
|
|
|
|
|||
Она определена для x D( y) . Поскольку y " = 0 при x = 0 , то
определив знак y " на каждом из интервалов
(−∞; −1), (-1;0), (0; +∞) , получим, что для x (−∞; −1) (−1;0)
y " < 0 , график выпуклый; для x (0; +∞) y">0 график вогну-
тый.
29
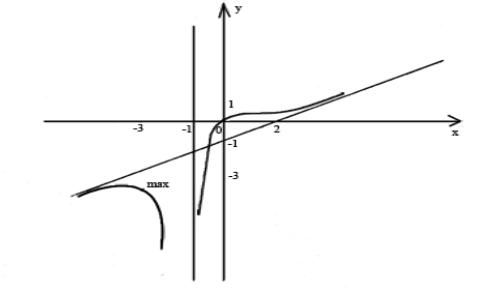
При переходе через точку x = 0 производная y " меняет знак, по-
этому x = 0 - точка перегиба, причём f (0) = 0 .
6. График функции пересекает координатные оси в т. (0;0) .
Задача 17. По формуле Тейлора с остаточным членом в форме Ла-
гранжа у функции ex вычислить значение с точностью до 0.001
при a1 = 0.1 a2 = 0.2 .
Решение: Формула Тейлора с остаточным членом в форме Лагранжа имеет вид
ex = 1 + |
x |
+ |
x2 |
+ |
x3 |
+ …+ |
xn |
+ R |
|
|
|
|
|||||
1! 2! |
3! |
|
n! |
n |
||||
|
|
|||||||
30
