
Контрольная по ВМатем
.pdf
е) уравнение прямой SD параллельной прямой АВ ж) площадь грани АВС
Решение:
а) Уравнение плоскости, проходящей через 3 точки
Принимает вид:
x − x1 |
y − y1 |
z − z1 |
|
x − 4 y − 2 z − 5 |
|
||
x2 − x1 |
y2 − y1 |
z2 − z1 |
= 0 , |
− 4 |
5 |
− 3 |
= 0 |
x3 − x1 |
y3 − y1 |
z3 − z1 |
|
− 4 |
0 |
2 |
|
10( x − 4) + 12( y − 2) + 20( z − 5) + 8( y − 2) = 0 10x + 12 y + 20z + 8 y − 180 = 0
x + 2 y + 2z − 18 = 0
б) Уравнение прямой АВ, как прямой, проходящей через две точки, запишется так
x − x1 = y − y1 = z − z1
x2 − x1 |
y2 − y1 |
z2 − z1 |
||||
|
x − 4 |
= |
y − 2 |
= |
z − 5 |
|
|
− 4 |
|
− 3 |
|||
|
5 |
|
||||
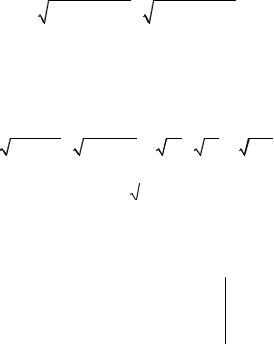
в) Уравнение высоты SN, опущенной из вершины S на плоскость АВС можно записать как уравнение прямой, проходящей через точку S и перпендикулярной плоскости АВС, имеющей нормальный
вектор n = (1, 2, 2) , который для этой прямой будет направляющим
SN: |
x −1 |
= |
y − 5 |
= |
z |
или |
|
|
|
||||
|
1 |
2 |
2 |
|
||
11
|
|
|
|
|
|
|
x = 1 + t |
|
|
|
|
|
||
|
|
|
|
|
|
|
y = 5 + 2t , t |
|
|
|
||||
|
|
|
|
|
|
|
z = 2t |
|
|
|
|
|
||
г) Найдем уравнение плоскости ВСS |
|
|
|
|||||||||||
|
x − 0 |
y − 7 |
z − 2 |
|
|
|
|
10x + 5( y − 7) + 5( z − 2) + 10x = |
||||||
|
|
|
|
|
||||||||||
|
0 |
−5 |
5 |
|
= 0, |
|
||||||||
|
|
|
= 20x + 5 y + 5z − 45 = 0 |
|||||||||||
|
1 |
−2 |
−2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
4x + y + z − 9 = 0 |
|
|
|
||||
Косинус угла найдем по формуле |
|
|
|
|
|
|||||||||
|
|
cosα |
= |
|
|
|
A1 A2 + B1B2 + C1C2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
A2 |
+ B2 |
+ C 2 |
* A2 |
+ B2 |
+ C 2 |
|||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
1 |
1 |
1 |
2 |
2 |
2 |
|
||||
Отсюда
cosα = |
1* 4 + 2 *1 + 2 *1 |
|
= |
|
8 |
|
|
= |
|
8 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 + 4 + 4 * 16 + 1+ 1 |
17 * 18 |
306 |
||||||||||||||
|
|
|
|
|
|
|||||||||||
|
|
α = arccos |
|
8 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
306 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
д) Объем пирамиды
|
1 |
|
x − x1 |
y − y1 |
z − z1 |
|||||
V = |
mod |
x |
− x |
y |
|
− y |
z |
|
− z |
|
|
2 |
2 |
||||||||
|
6 |
|
2 |
1 |
|
1 |
|
1 |
||
|
|
x3 |
− x1 |
y3 − y1 |
z3 − z1 |
|||||
|
|
|
||||||||
12

|
|
|
1 |
|
0 − 4 |
7 − 2 |
2 − 5 |
|
|
|
1 |
|
|
−4 5 −3 |
|
|||||||||
V = |
mod |
0 |
− 4 |
2 − 2 |
7 − 5 |
= |
mod |
−4 0 |
2 |
= |
||||||||||||||
|
|
|
||||||||||||||||||||||
|
|
|
6 |
|
1 |
− 4 5 − 2 0 − 5 |
6 |
|
|
−3 3 |
−5 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
= |
1 |
|
36 − 30 + 24 −100 |
|
= |
1 |
|
|
−70 |
|
= |
70 |
|
|
|
|||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
6 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
6 |
|
|
|
|
|||||
е) Т.к. прямая SД параллельна АВ, то направляющие векторы пря-
мых совпадают l = (−4, 5, −3). Составим уравнение прямой SД, проходящий через точку S(1,5,0)
x −1 |
= |
y − 5 |
= |
z |
−4 |
|
−3 |
||
5 |
|
|||
ж) Площадь грани вычислим по формуле |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S = |
|
AB, AC |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
i |
j |
k |
|
|
|
5 3 |
|
|
−4 −3 |
|
−4 5 |
|
|||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
AB, AC |
|
= |
−4 5 −3 |
= i |
− j |
+ k |
= |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2 |
|
|
−4 2 |
|
−4 0 |
|
|
|
|
|
−4 |
0 |
|
2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= 10i + 20 j + 20k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||
|
|
|
S = |
102 + 202 + 202 = 15 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 8. Привести к каноническому виду уравнение кривой
5x2 + 4xy + 8 y 2 + 8x +14 y + 5 = 0 и найти формулы преобразования координат.
13

Решение: Обозначим L( x, y) = 5x2 + 4xy + 8 y2 |
|
|
||||
Матрица этой квадратичной формы имеет вид |
5 |
2 |
||||
|
|
|||||
|
|
|
|
|
2 |
8 |
Составим характеристическое уравнение матрицы |
|
|||||
|
5 − λ |
2 |
|
= λ 2 −13λ + 36 |
= 0 |
|
|
|
|
||||
|
2 |
8 − λ |
|
|
||
|
|
|
|
|
||
|
|
|
|
|
|
|
Откуда λ1 = 4, λ2 = 9
Найдем собственные векторы. Для λ = 4 имеем систему уравнений
α |
+ 2α |
|
= 0 |
1 |
|
2 |
α1 = −2α2 |
2α1 + 4α2 = 0
Тогда xα = (2t, −t ), t ≠ 0, t |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Нормируя полученные векторы, находим |
|||||||||||||
x′ |
= ( |
2 |
; − |
|
1 |
|
) |
||||||
|
|
|
|
|
|
|
|||||||
α1 |
|
|
|
|
5 |
|
|
|
|
5 |
|
||
Для α 2 = 9 получаем систему |
|
|
|
|
|
|
|
|
|
|
|
|
|
−4α1 + 2α |
2 |
= 0 |
α2 = 2α1 |
||||||||||
|
|
|
|
|
|
|
|||||||
2α1 − α2 |
= 0 |
|
|
|
|
|
|
|
|
|
|
||
′ |
|
|
|
|
|
|
|
|
|
||||
Следовательно, xα1 = (t, 2t), t |
≠ |
0, t |
|
|
|
|
|
|
|
|
|
||
Нормируя полученные векторы, имеем |
|
|
|
|
|||||||||
x |
|
= ( |
1 |
; |
2 |
) |
|||||||
|
|
|
|
|
|||||||||
α2 |
|
|
|
5 |
|
|
|
5 |
|
|
|||
Таким образом, матрица преобразования координат
|
|
|
2 |
|
|
|
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
5 |
|
|
5 |
||||||
T = |
|
|
|
|
|
|
|||||
|
− |
1 |
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||
5 |
|
5 |
|
||||||||
|
|
|
|
|
|
||||||
формулы преобразования осей координат имеют вид
14

|
2 |
|
|
x′ + |
1 |
|
|
y′ |
|
|
||||||
x = |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
5 |
|
|
|
|
5 |
|
|
|
|
, а |
(1) |
||||
|
|
|
1 |
|
|
|
2 |
|
||||||||
y = − |
x′ + |
y′ |
|
|
||||||||||||
|
|
|
|
|
|
|||||||||||
|
5 |
|
5 |
|
|
|
||||||||||
|
|
|
|
|
||||||||||||
Подставив в уравнение данной кривой выражения для x и y из (1), |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5( |
2 |
|
|
x′ + |
|
1 |
|
|
y ′)2 + 4( |
2 |
|
x′ + |
1 |
|
|
y ′)(− |
x |
′ |
|
+ |
2 |
y ′ |
) + 8(− |
x |
′ |
|
+ |
2 |
y ′ |
)2 + |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
5 |
|
|
|
|
|
|
5 |
|
|
5 |
|
|
|
|
|
|
5 |
5 |
|
5 |
5 |
|
|
|
5 |
|
|
||||||||||||||||||||||||||||
+8( |
2 |
|
|
x′ + |
1 |
|
|
y ′) + 14(− |
|
x |
′ |
|
+ |
2 |
y ′ |
) + 5 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
5 |
|
|
|
5 |
|
|
|
|
5 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
После несложных преобразований получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x′2 + 9 y′2 + |
2 |
|
x′ + |
36 |
|
y′ + 5 = 0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Применив метод выделения полного квадрата, получим:
4( x′2 + |
|
x′ |
|
) + 9( y′2 + |
4 |
|
y′) + 5 = 0, |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
2 |
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
4(( x′ + |
|
1 |
|
|
|
|
|
)2 − |
1 |
) + 9(( y′ + |
2 |
|
)2 − |
4 |
) + 5 = 0, |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
4 |
5 |
|
80 |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
5 |
|
|
||||||||||||||
4( x′ + |
|
1 |
|
|
|
|
)2 + 9( y′ + |
2 |
|
)2 + 5 − |
1 |
− |
36 |
= 0, |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
4 |
|
5 |
|
|
|
5 |
|
|
|
|
20 |
|
5 |
|
||||||||||||||||||||
4( x′ + |
|
1 |
|
|
|
|
)2 + 9( y′ + |
2 |
|
)2 = |
9 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
4 |
|
5 |
|
|
|
5 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
||||||||||||||
С помощью формулы параллельного переноса
x′ = x′′ − |
1 |
|
|
||
|
|
|
|
|
|
|
4 5 |
||||
|
2 |
|
|
||
y′ = y′′ − |
|
|
|||
|
|
|
|
|
|
|
5 |
|
|||
|
|
||||
15

получаем
4x′′2 + 9 y′′2 = |
9 |
|
x′′2 |
y′′2 |
|||
|
или |
|
+ |
|
= 1 |
||
4 |
9 16 |
1 4 |
|||||
|
|
|
|
||||
Это уравнение эллипс с полуосями a = 3 , b = 1 4 2
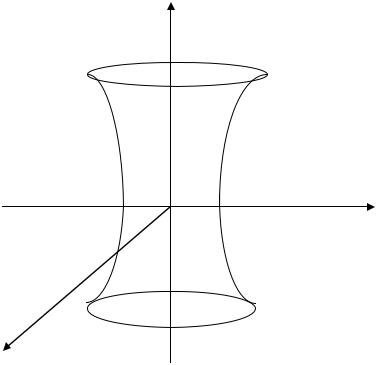
Задача 9. Методом параллельных сечений исследовать форму поверхности
x2 + y 2 − z 2 = 36
Решение: Будем пересекать поверхность горизонтальными плоскостями z = h .
Подставим z = h в уравнение. Получим
x2 + y 2 = h2 + 36
Откуда видно, что любом таком сечении получаются окружности
радиуса 
 h2 + 36 , наименьшая из которых имеет радиус равный 6(h=0). Сечение плоскостями x=с дает гиперболы
h2 + 36 , наименьшая из которых имеет радиус равный 6(h=0). Сечение плоскостями x=с дает гиперболы
y2 − z 2 = 36 − c2
Сечение плоскостями y = a , также дает гиперболы x2 − z 2 = 36 − a2
Координатные плоскости являются плоскостями симметрии. Поверхность изображена на рисунке
16
Задача 10: Найти предел функции не пользуясь правилом Лопиталя.
Решение: |
|
|
|
|
|
|
|
|
|
|
||
а) |
|
|
|
|
|
|
|
|
|
|
|
|
lim |
x2 |
− 3x + 2 |
= lim |
( x − 1)( x − 2) |
= lim |
x −1 |
= |
2 −1 |
|
= |
1 |
= −1 |
x→2 x2 |
− 5x + 6 |
x→2 |
( x − 2)( x − 3) |
x→2 x − 3 |
|
2 − 3 |
|
−1 |
||||
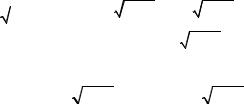
б)
17
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10x2 |
|
|
|
|
3x |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
1 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
10x2 |
|
|
− 3x − 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 − |
|
|
− |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
lim |
|
|
|
|
|
= lim |
|
|
|
|
x2 |
x2 |
|
x2 |
|
|
|
= lim |
x |
x2 |
= |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
x→∞ 5x2 |
+ 128x + 4 |
|
|
x→∞ 5x2 |
|
|
|
|
128x |
|
|
|
|
|
4 |
|
|
|
|
|
|
x→∞ |
5 + |
128 |
+ |
4 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 + |
|
|
|
x2 |
|
+ x2 |
|
|
|
|
|
|
|
|
|
x |
|
x2 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
lim10 − lim |
3 |
|
− lim |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 − 0 − 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
= |
|
x→∞ |
|
|
|
|
|
|
x→∞ x |
|
|
|
x→∞ x2 |
|
= |
= 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
128 |
|
|
|
|
|
|
|
4 |
5 + 0 + 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
lim 5 + lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
+ lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
x |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
x→∞ |
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
x→∞ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
в) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
− 3)( |
|
|
|
|
+ 3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + 8 |
x + 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x + 8 − 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
lim |
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
x→1 |
|
x |
2 |
− x |
|
|
|
|
|
|
|
|
|
|
x→1 |
|
|
x ( x − 1)( x + 8 + 3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= lim |
|
|
|
|
|
|
|
|
|
x + 8 − 9 |
|
|
|
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
= |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
x→1 x ( x − 1)( |
x + 8 |
+ 3) |
|
|
|
x→1 x ( |
x + 8 |
+ 3) |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
г) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
tg 2x |
|
|
= lim |
|
tg 2x 3x 2x |
|
= lim |
|
|
tg 2x |
|
|
3x |
|
|
|
2 |
|
= 1 1 |
2 |
= |
2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x→0 sin 3x |
|
|
x→0 sin 3x 3x 2x |
|
x→0 |
|
|
|
2x |
|
|
|
sin 3x |
|
|
3 |
|
|
|
|
3 3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
д) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + 1 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − 1 + 1 + 1 x |
|
|
|
|
|
|
|
|
|
( x − 1) + 2 x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
lim |
|
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
x→∞ x − 1 |
|
|
|
|
x→∞ |
|
|
|
|
|
x − 1 |
|
|
|
|
x→∞ |
|
|
|
|
x − 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x −1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x−1 |
|
|
2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
x −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
x −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
= lim |
1 |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
1 |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
x→∞ |
|
|
|
|
|
|
|
x − |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
x − |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 x |
|
|
|
lim |
2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
= lim e x−1 |
|
|
|
|
= e2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
= ex→∞ x −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Задача 11. Найти производную заданной функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
а) y = |
ex |
− ln x |
+ arcsin2 (ln (a3 + x3 )) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ex |
+ ln x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
18

б) y = ex cos x + e  ln(ax2 +bx+c)
ln(ax2 +bx+c)
в) y = (sin x )cos x
г) y = 1 + xe y
Решение:
Применяя правила дифференцирования и используя таблицу производных, находим:
|
x |
− ln x |
' |
|
' |
|
y ' = |
e |
|
|
+ (arcsin2 (ln (a3 + x3 ))) |
= |
|
|
|
|
||||
ex |
+ ln x |
|
|
|||
а) |
(ex − ln x )' (ex + ln x ) − (ex − ln x )(ex + ln x )' |
|
|
|
||||||||||||||||||||||||||
= |
|
|
|
|
|
|
(ex |
|
+ ln x )2 |
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
+2 arcsin (ln (a3 |
+ x3 )) (arcsin ln (a3 |
+ x3 ))' |
= |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
ex − |
|
|
(ex + ln x ) − (ex − ln x ) ex + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
= |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
x |
|
|
+ |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
(ex + ln x )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
+2 arcsin (ln (a3 |
+ x3 )) |
|
|
|
1 |
|
|
|
|
1 |
|
|
(a3 |
+ x3 ) |
' |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 − ln2 (a3 + x3 ) a3 + x3 |
|
|
|
|
|
|
||||||||||||||
|
e2 x − |
ex |
+ ex ln x − |
ln x |
|
− e2 x + ln x ex − |
ex |
|
+ |
ln x |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
= |
|
|
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
x |
|
|
|
x |
+ |
|
||||||
|
|
|
|
|
|
(ex |
+ ln x )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
+2 arcsin (ln (a3 |
+ x3 )) |
|
|
|
3x2 |
|
|
|
|
|
× |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1 − ln2 (a3 + x3 ) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
19
|
|
|
|
|
|
|
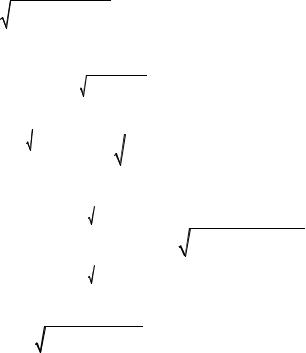
2ex ln x − 2 |
ex |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
× |
|
|
|
|
1 |
= |
x |
|
+ 2 arcsin(ln (a3 |
+ x3 )) * |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
a3 |
|
+ x3 |
|
(ex + ln x )2 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
* |
|
|
|
|
|
|
|
3x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(a3 + x3 ) 1 − ln2 (a3 + x3 ) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
' |
|
|
|
|
|
|
|
|
||||
y ' = (ex |
cos x ) |
' |
|
|
ln(ax2 +bx +c) |
= ex |
cos x − |
|
|
|
||||||||||||||||||||
|
|
+ e |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
)' |
|
|
|
||||||||||||||
|
|
|
sin x + e ln(ax2 +bx +c ) |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
−ex |
|
|
ln (ax2 |
+ bx + c ) |
= |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(ln (ax 2 + bx + c ))' |
|||||||||||
= e x |
(cos x − sin x ) + e |
ln (ax 2 + bx + c ) |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
ln (ax 2 + bx + c ) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= e x |
(cos x − sin x ) + e |
ln (ax 2 + bx + c ) |
* |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
* |
|
|
|
|
|
|
|
(2ax + b )' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 (ax2 + bx + c ) ln (ax2 + bx + c ) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
в) |
y = (sin x )cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Прологарифмируем обе части: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
ln y = ln (sin x )cos x |
|
|
|
|
ln y = cos x ln sin x |
|
|
|
||||||||||||||||||||||
Продифференцируем обе части
20
