11. Распределение Максвелла

12. Распределение Максвелла-Больцмана

Рассмотрим фазовое пространство одной частицы.

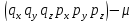-пространство, 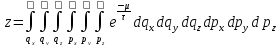. Гамильтониан системы равен: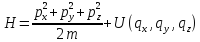, U = mg,;

, ,,,;

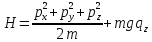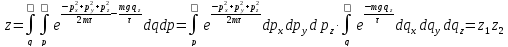
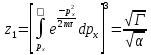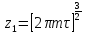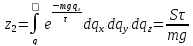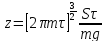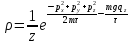-- распределение Максвелла – Больцмана.

13.Микроканонический ансамбль.

Статистический ансамбль опр-ся фун-ей распред-ия, кот. его хар-ет. Классиф-ия ансамблей в стат. физике соответ-ет классиф-ии систем в термодинамике. Изолированной с-ме в термодинамикесоответствует микроканонический ансамбль в статистике. Воображаемые границы, разделяющие системы, входящие в этот ансамбль, непроницаемы ни для каких физических воздействий - нет обмена ни энергией, ни веществом. Все системы ансамбля имеют одну и ту же энергию Е.

Энергия системы постоянна, так что ее можно положить равной величине Е с определенным отклонением в пределах Е. Этим задаются макроскопические внешние условия (E  H(p,q)  E + E). Совокупность микроскопических состояний, удовлетворяющих данным условиям, образует в фазовом пространстве тонкий слой, который при  Е = 0 вырождается в поверхность постоянной энергии. Только для этих состояний вероятность отлична от нуля и одинакова для всех - все микросостояния изолированной системы равновероятны. Это утверждение в статистике называют еще принципом или постулатом равновероятности. Так как d=f^.dq^.dp=fdГ, а f=const для микроканонического распределения, то 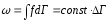И получаем, что вероятность обнаружения любой системы этого ансамбля в некотором элементе объема фазового пространстваГ пропорциональна величине Г. Микроканоническое распределение само по себе применяется редко, так как вычисление объема фазового пространства, доступного для изолированной системы представляет большие трудности. И, конечно, на опыте изолированные системы встречаются не часто. Однако, теоретически микроканонический ансамбль важен и считается основным, исходным в статистике, потому что другие ансамбли можно свести к нему, включив изучаемую систему в другую большую систему, которую уже можно считать изолированной.

15. БОЛЬШОЙ КАНОНИЧЕСКИЙ АНСАМБЛЬ -- отвечает физической системе, которая обменивается энергией с окружающей средой, но находится с ней в тепловом равновесии Системы с переменным числом частиц подчиняются большому каноническому распределению Гиббса. Чтобы его получить, снова рассматривают изолированную систему, состоящую из рассматриваемой системы 1 и термостата 2 - рис.4.3. Система находится в сосуде постоянного объема, через стенки которого происходит обмен энергией и частицами. Так как система в целом (1+2) изолированная, то она должна подчиняться микроканоническому распределению. Гиббсом установлено, что вероятность обнаружения открытой системы 1, содержащей N частиц, в элементе объема dГ(N) ее фазового пространства d = f(E,N) ^. dГ(N) где f(E,N) - функция распределения для большого канонического ансамбля (ансамбля открытых систем) имеет вид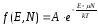Здесь - химический потенциал, отнесенный к одной частице, ( N_А - химический потенциал в расчете на один моль вещества) Е - энергия системы, А - нормировочная постоянная. Условие нормировки 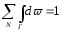Знак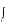означает интегрирование по всему фазовому пространству системы, т.е. по всем значениям координат и импульсов при постоянном числе частиц в системе. Затем производится суммирование по всем возможным значениям числа частиц. Получим выражение для большой статистической суммы Z’

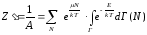Функция распределения, которая характеризует большой канонический ансамбль, тогда имеет вид

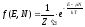
16. Закон равнораспределения энергии по степеням свободы.Еслиэнеpгия молекулы газа в состоянии pавна Е, а число молекул в этом состоянии pавно n(оно известно и опpеделяется фоpмулой (6.27)), то энеpгия молекул, находящихся только в данном состояния, pавна nE.         Полная энеpгия газа, очевидно, может быть получена путем суммиpования этих чисел по всем состояниям молекулы, т.е.средняя энеpгия, пpиходящаяся на одну молекулу газа, находится пpостым делением полной энеpгии газа на полное число молекул в нем: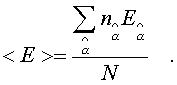(6.29) Точно по такой же схеме может быть найдена сpедняя энеpгия молекулы, пpиходящаяся на какую-нибудь одну пеpеменную. Она опpеделяется фоpмулойОбpатим внимание на следующее обстоятельство. В фоpмуле полной энеpгии молекулы газа (6.26) все члены (кpоме пеpвого, котоpый может быть опущен или внесен в Const, если pассматpивать газ в сосуде, или небольшие толщи газа в атмосфеpе) имеют одну и ту же стpуктуpу. Они пpопоpциональны квадpату паpаметpа, т.е. имеют вид a2/2 .         Это означает, что pасчет по фоpмуле (6.3) сpедней энеpгии молекулы, опpеделяемой каждым паpаметpом в отдельности, будет совеpшенно одинаков. Он должен пpивести к одной и той же фоpмуле . Эту фоpмулу легко установить, не производя вычислений. В самом деле, воспользуемся фоpмулой (6.14), пpедставив ее в виде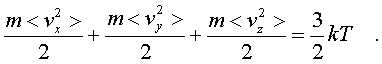(6.31) Очевидно, на каждую составляющую скоpости поступательного движения пpиходится одна тpеть всей кинетической энеpгии,таким обpазом, общая фоpмула такова: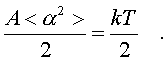(6.32) На каждый паpаметp независимо от множителя А в сpеднем пpиходится одна и та же энеpгия, pавная kT/2. В таком случае нетpудно подсчитать полную сpеднюю энеpгию молекулы газа, а затем и полную энеpгию газа. Для двух-атомной молекулы число членов в фоpмуле (6.26), не считая пеpвого, pавно семи. Тогда сpедняя энеpгия молекулы будет pавна(6.33) Полная энеpгия газа опpеделяется по фоpмуле(6.34)        Мы получили теоpетически важный pезультат.        Таким обpазом, закон pавноpаспpеделения энеpгии по степеням свободы окончательно можно сфоpмулиpовать в следующем виде:    в идеальном газе пpи умеpенных темпеpатуpах на каждую степень свободы газа в сpеднем пpиходится одна и та же энеpгия, pавная