
- •1.Исторический обзор развития термодинамики и статистической физики.
- •2.Простые модельные системы. Конфигурации. Макросостояние и микросостояние системы. Однородное и неоднородное состояние системы
- •3.Распределение вероятностей для случайной физической величины. Теоремы сложения и умножения вероятностей.
- •4. Понятие вероятности. Статистическая независимость и квадратичная флуктуация
- •5.Равновесное и неравновесное состояния системы. Флуктуации. Необратимость. Энтропия.
- •6.Классическое описание движения механических систем. Канонические уравнения движения гамильтона
- •7.Фазовое пространство. Точка фазового пространства. Объем фазового пространства. Фазовая траектория. Статистический ансамбль.
- •8.Теорема лиувилля. Функция статистического распределения
- •11. Распределение Максвелла
- •12. Распределение Максвелла-Больцмана
- •13.Микроканонический ансамбль.
- •17. Уравнение состояния идеального газа
- •18. Одноатомный идеальный газ.
- •19. Двухатомный идеальный газ. Вращательная и колебательная степени свободы.
- •20.Классическая теория теплоемкости многоатомного идеального газа.
- •23.25. Квантово-механическое описание систем. У.Ш. Рассчет числа возможных состояний ид.Газа.
- •29.21 Теплоемкость твердых тел. Теория эйнштейна.
- •30. Теплоемкость твердых тел. Теория Дебая.
- •31. Теория флуктуаций
- •32.Термодинамическая система. Равновесные состояния и равновесные процессы. Температура. Нулевое начало.
- •33.Изопроцессы. Работа.
- •35. Теплоемкость газа.
- •36. Круговые процессы. Цикл Карно.
- •38. Процесс джоуля-томсона
- •40. Второе начало термодинамики.
- •41.Энтропия. З-н возраст.Э-пии
- •42. Неравенство клаузиуса. Общие условия термодин-го равновесия и устойчивости однородной системы.
- •43. Третье начало термод. И его следствия
- •44.Системы с переменным количеством вещества. Химический потенциал.
- •45.Равновесие фаз. Фазовые переходы первого рода
- •47. Броуновское движение. Уравнение фоккера-планка
- •48. Фазовые переходы второго рода. Теория ландау
- •51.Явления переноса. Уравнение фурье. Нестационарное уравнение теплопроводности.
- •52. Каноническое распределение и термодин. Функции.
6.Классическое описание движения механических систем. Канонические уравнения движения гамильтона
Классич.
механика позволяет рассчитать харак-ки
движения взаимод-щих тел (частиц) на
основе 2 з-на Ньютона. Частицы движутся
по определенным траекториям. С траекториями
связаны такие характеристики, как
координаты, скорости частицы и ускорение.
При извест-х силах, действующих на i-тую
частицу, зад-ых нач. условиях (координаты
и скорости частицы в нач. момент времени)
в механике Ньютона нет места
неопределенности, вероятности,
случайности, потому что интегрирование
уравнения движения однозначно позволяет
найти скорости и координаты частицы в
любой момент времени. Современная физика
обычно использует не ньютоновское
описание состояния в механике, а
представление Гамильтона. При этом
вводятся новые, обобщенные координаты
(их обозначают
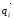 )
и обобщенные импульсы(
)
и обобщенные импульсы(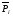 ).Они
являются независимыми переменными.
).Они
являются независимыми переменными.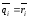 ,
,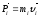 .
Введение новых независимых переменных
приводит к существенному упрощению
уравнений движения. Центральная величина
динамики в представлении Гамильтона -
энергия системы, записанная в этих
переменных. Для консервативных систем
полная энергия системы Е равна сумме
кинетической энергии, зависящей только
от импульсов и потенциальной энергии,
зависящей только от координат. Эту
энергию называютфункцией
Гамильтона
или гамильтонианом
H.
Для системы из N
взаимодействующих частиц она равна
.
Введение новых независимых переменных
приводит к существенному упрощению
уравнений движения. Центральная величина
динамики в представлении Гамильтона -
энергия системы, записанная в этих
переменных. Для консервативных систем
полная энергия системы Е равна сумме
кинетической энергии, зависящей только
от импульсов и потенциальной энергии,
зависящей только от координат. Эту
энергию называютфункцией
Гамильтона
или гамильтонианом
H.
Для системы из N
взаимодействующих частиц она равна
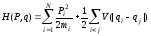 ЗдесьV
- потенциальная энергия взаимодействия
i-той
и j-той
частицы, которые связаны между собой
силами
ЗдесьV
- потенциальная энергия взаимодействия
i-той
и j-той
частицы, которые связаны между собой
силами
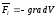 .Определение
для скорости частицы и второй закон
Ньютона эквивалентны следующим
выражениям
.Определение
для скорости частицы и второй закон
Ньютона эквивалентны следующим
выражениям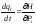 ,
,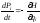 Их называютуравнениями
Гамильтона или каноническими уравнениями
движения.
При таком описании число независимых
переменных и число уравнений удваивается,
но сами уравнения движения упрощаются
- это уравнение первого, а не второго
порядка, как во втором законе Ньютона.
Кроме того, решение уравнения удобно
изображать фазовой
точкой
с координатами
Их называютуравнениями
Гамильтона или каноническими уравнениями
движения.
При таком описании число независимых
переменных и число уравнений удваивается,
но сами уравнения движения упрощаются
- это уравнение первого, а не второго
порядка, как во втором законе Ньютона.
Кроме того, решение уравнения удобно
изображать фазовой
точкой
с координатами
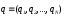 и
и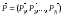 вN
- мерном пространстве, которое называют
фазовым
пространством
и которым принято пользоваться при
описании колебательных систем. С течением
времени частицы системы, взаимодействуя
друг с другом, меняют свое состояние, а
фазовая точка будет двигаться в фазовом
пространстве в соответствии с уравнениями
движения (Д3). В силу теоремы о единственности
решения дифференциальных уравнений
траектория движения фазовой точки не
пересекается сама
вN
- мерном пространстве, которое называют
фазовым
пространством
и которым принято пользоваться при
описании колебательных систем. С течением
времени частицы системы, взаимодействуя
друг с другом, меняют свое состояние, а
фазовая точка будет двигаться в фазовом
пространстве в соответствии с уравнениями
движения (Д3). В силу теоремы о единственности
решения дифференциальных уравнений
траектория движения фазовой точки не
пересекается сама
7.Фазовое пространство. Точка фазового пространства. Объем фазового пространства. Фазовая траектория. Статистический ансамбль.
Будем считать, что мгновенные значения каждой координаты (импульса) каждой частицы отклад-ся на своей корд. оси. С-ма координат, образ-ая этими осями, будет хар-вать нек. воображаемое математич. прост-во. Его наз. фазовым или Г-простр-вом. Его размерность равна удвоенному числу степеней свободы. Мгновенное состояние с-мы в ФП (микросостояние) изображается фаз. точкой, кот. задает в данный момент времени состояние всех частиц системы, т.е. положение их в простр-ве и их импульсы. Изменение состояния с-мы с теч. времени изобр-ся в ФП кривой qi(t), pi(t), кот. наз. фаз. траекторией. Т.о., микросостояния образуют непрерыв. совок-сть точек в ФП. Таким образом, в то время как при детальном динамическом описании состояние системы представляется одной точкой движущейся с фазовой скоростью в фазовом пространстве 2s измерений, где s число степеней свободы системы, в статистическом подходе состояние системы задается совокупностью точек в фазовом пространстве, причем каждая из них характеризуется определенным весом. Такую совокупность точек с весом называют статистическим ансамблем.
Т.е. статистический ансамбль - это множество копий рассматриваемой системы, представляющих все ее различные возможные микроскопические состояния, в данный момент времени t.
