
- •1.Источники и классификация погрешностей. Неустранимая и вычислительная погрешность.
- •2. Постановка задачи интерполирования. Существование и единственность обобщенного интерполяционного многочлена.
- •3. Интерполяционный многочлен Лагранжа.
- •4. Схема Эйткина
- •5. Остаточный член интерполяционного многочлена Лагранжа.
- •6. Минимиз. Оценки остаточного члена интерпол. Мн-на.
- •7. Разделенные разности и интерполяционная формула Ньютона с разделенными разностями.
- •8. Конечные разности и интерполяционные формулы Ньютона с конечными разностями.
- •9. Составление таблиц.
- •10. Сходимость интерполяционного процесса
- •11.Общая задача интерполирования алгебраическими многочленами. Интерполяционный многочлен Эрмита с узлами кратности 2.
- •13 . Оптимизация шага при численном диф-нии
- •14. Интерполяционные квадратурные формулы
- •15. Квадратурные формулы Ньютона-Котеса
- •16. Простейшие квадрат ф-лы н-Кот. И оценка их погрешности.
- •17. Составные квадратурные формулы средних прямоугольников, трапеций, парабол и оценка их погрешности
- •18. Квадратурные формулы Гаусса
- •20. Метод наименьших квадратов.
- •22.Обобщённые мног-ны наилучших среднеквадратических приближений.
- •24. Многочлены наилучших равномерных приближений. Примеры.
- •25. Наилучшие приближения в линейном нормированном пространстве.
- •26. Интерполяционные сплайны.
- •27. Существование и единственность кубического сплайна.
- •28.Краткие сведения о нормах векторов и матриц.
- •29. Обусловленность линейных алгебраических систем.
- •30. Метод Гаусса решения системы линейных ур-ний.
- •31. - Разложение квадратных матриц.
- •32. Разложение симметричных матриц. Метод квадр. Корней решения лин. Алг.Систем
- •34. Принцип сжимающих отображений в метрическом пространстве.
- •35. Метод простой итерации решения лин. Алг. Систем и усл. Его сходимости.
- •36. Метод Якоби решения линейных алгебраических систем
- •37. Метод Зейделя решения лин. Алг. Систем.
- •38. Метод покоординатного спуска решения линейных алгебраических систем.
- •39. Метод скорейшего спуска решения линейных алгебраических систем
- •40. Степенной метод решения частичной проблемы собственных значений.
- •41. Метод Данилевского раскрытия характеристического уравнения
- •42. Метод вращений решения полной проблемы собственных значений.
- •43. Метод бисекции и простой итерации решения уравнений с одним неизвестным.
- •44. Методы хорд и касательных как частные случаи метода простой итерации.
- •45. Методы локализации корней алгебраического уравнения.
- •46. Метод Лобачевского решения алгебраических уравнений.
- •47. Методы простой итерации и Зейделя решения системы нелинейных уравнений.
- •48. Метод Ньютона и аналоги метода Зейделя решения системы нелинейных уравнений.
- •49. Классификация численных методов решения задачи Коши. Методы Эйлера, трапеций и к-э.
- •50. Метод Рунге-Кутта решения задачи Коши. Построение методов р-к второго порядка точности.
- •51. Оценка погрешности и сходимость одношаговых методов решения задачи Коши.
- •52. Экстраполяц. Метод Адамса решения задачи Коши.
- •53. Интерполяционный метод Адамса решения задачи Коши.
- •54. Общий вид линейных многошаговых методов решения задачи Коши.
- •55. Условие корней многошаговых методов решения задачи Коши
- •56. Сходимость многошаговых методов решения Коши.
- •57. Сеточные методы решения краевых задач для обыкновенных дифференциальных уравнений.
- •58. Сходимость сеточного метода решения краевых задач для обыкновенных диф. Уравнений.
- •59. Методы прогонки и пристрелки решения разностных схем при решении краевых задач для обыкновенных д.У.
- •60. Эквивалентность граничных и вариационных задач
- •61. Метод Ритца решения вариационных задач.
- •62. Построение системы линейных уравнений для определения значений параметров в методе Ритца.
- •63. Вариационно-разностный вариант метода Рица.
- •64. Сеточные методы решения краевой задачи для уравнения Пуассона. Фоpмулиpовка исходной диффеpенциальной краевой задачи
- •Постpоение pазностной схемы
- •65. Основные понятия теории разностных схем.
- •66. Сходимость сеточного метода
- •Фоpмулиpовка исходной дифференциальной краевой задачи
- •67.Метод матричной прогонки решения разностной схемы. Фоpмулиpовка исходной диффеpенциальной краевой задачи
- •68. Разностные схемы для одномерного параболического уравнения. Фоpмулиpовка исходной диффеpенциальной задачи
- •69. Разностные схемы решения задачи Коши для уравнения гиперболического типа.
- •70. Сеточные методы решения смешанной задачи для уравнений гиперболического типа.
- •71. Метод квадратур решения интегрального уравнения Фредгольма 2-го рода.
- •72. Решение интегрального уравнения Фредгольма 2-го рода с вырожденным ядром.
- •Решение интегр. Ур-ния с вырожденным ядром.
- •73. Решение интегрального уравнения Фредгольма 2-го рода методом вырожденного ядра.
- •Способы приближения невырожденного ядра вырожденным.
16. Простейшие квадрат ф-лы н-Кот. И оценка их погрешности.
Пример 1.
Положим
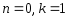 .
В этом случае
.
В этом случае
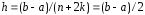 ;
;
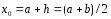 ;
;
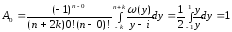
и получаем
квадратурн. ф-лу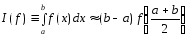 (1)
(1)
Квадратурную формулу (1) наз-ют квадратурной формулой ср. прямоугольников, т.к. здесь интеграл приближается площадью (квадратурой) прямоугольника с шириной, равной длине отрезка интегрирования, и высотой, равной значению подынтегральной функции в середине отрезка интегрирования.
Используя
разложение подынтегральной функции в
ряд Тэйлора в точке
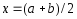 ,
имеем
,
имеем
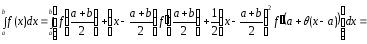
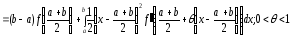 .
.
Отсюда для погрешности квадратурной формулы получаем выражение
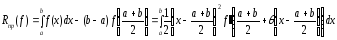 Применение
теоремы о среднем дает (2):
Применение
теоремы о среднем дает (2):
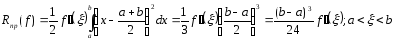 Пример
2. Положим
Пример
2. Положим
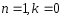 .
В этом случае
.
В этом случае
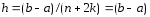 ;
;
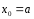 ;
;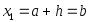 ;
;
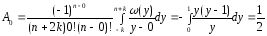 ;
;
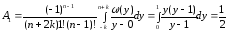 .
.
и получаем квадратурную формулу
 . (3)
. (3)
Квадратурную формулу (3) называют квадратурной формулой трапеций, потому что здесь интеграл приближается площадью трапеции с высотой, равной длине отрезка интегрирования, и основаниями, равными значениям подынтегральной функции на концах отрезка интегрирования.
Подынтегральную
функцию выразим через ее интерполяционный
многочлен по узлам
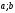 и остаточный член интерполяционного
многочлена. Тогда получим
и остаточный член интерполяционного
многочлена. Тогда получим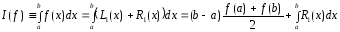 Отсюда
для погрешности квадрат. ф-лы трапеций
получ. выр.
Отсюда
для погрешности квадрат. ф-лы трапеций
получ. выр.
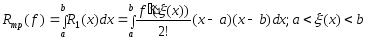 Применяя
теорему о среднем, имеем
Применяя
теорему о среднем, имеем
 . (4)
. (4)
Пример 3.
Положим
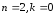 .
В этом случае
.
В этом случае
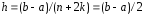 ;
;
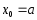 ;
;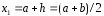 ;
;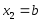 ;
;
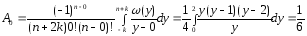 ;
;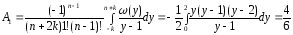 ;
;
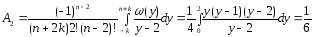 .
.
и получаем квадратурную формулу
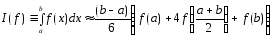 . (5)
. (5)
Квадратурную
формулу (5) называют квадратурной формулой
парабол или квадратурной формулой
Симпсона. Здесь интеграл от функции
приближается интегралом от интерполяционного
многочлена второй степени (параболы) с
узлами
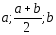 .
Погрешность квадратурной формулы (5)
запишем в виде
.
Погрешность квадратурной формулы (5)
запишем в виде
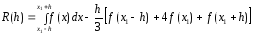 , (6)
, (6)
где
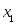 будем считать константой, аh
– переменной. Очевидно,
будем считать константой, аh
– переменной. Очевидно,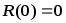 .Выполним
дифференцирование равенства (6) поh:
.Выполним
дифференцирование равенства (6) поh:
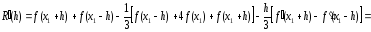
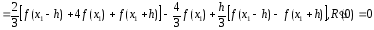 Проводя
дифференцирование еще два раза и
используя формулу конечных приращений,
получим
Проводя
дифференцирование еще два раза и
используя формулу конечных приращений,
получим
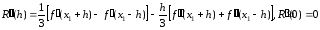 ,
,
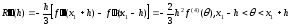 . (7)
. (7)
Проводя три раза интегрирование и используя при этом теорему о среднем, имеем
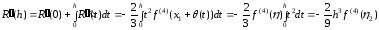 ,
,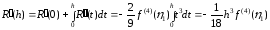 ,
,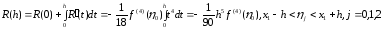 Полученное
выражение для остаточного члена
перепишем в виде
Полученное
выражение для остаточного члена
перепишем в виде
17. Составные квадратурные формулы средних прямоугольников, трапеций, парабол и оценка их погрешности
Как
видно из выражения (2) предыдущего
параграфа, погрешность квадратурной
формулы средних прямоугольников есть
величина третьего порядка относительно
длины
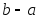 отрезка интегрирования. Таким образом,
при большой длине отрезка интегрирования
погрешность указанной квадратурной
формулы также может быть большой.На
отрезке
отрезка интегрирования. Таким образом,
при большой длине отрезка интегрирования
погрешность указанной квадратурной
формулы также может быть большой.На
отрезке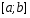 введем равномерную сетку
введем равномерную сетку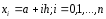 с шагом
с шагом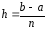 .
Интеграл по всему отрезку равен сумме
интегралов по частичным отрезкам.
Применяя квадратурную формулу средних
прямоугольников в случае четного
.
Интеграл по всему отрезку равен сумме
интегралов по частичным отрезкам.
Применяя квадратурную формулу средних
прямоугольников в случае четного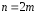 к частичным отрезкам
к частичным отрезкам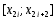 ,
имеем
,
имеем
 .
.
Полученную
квадратурную формулу
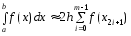 (1)
(1)
называют составной квадратурной формулой средних прямоугольников.
Для погрешности составной квадратурной формулы средних прямоугольников получаем
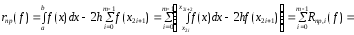
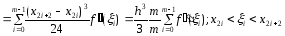 .
.
Учитывая,
что
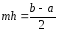 и
и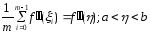 ,
отсюда следует искомое равенство
,
отсюда следует искомое равенство . (2)
. (2)
Используя
квадратурную формулу трапеций при
интегрирования по частичным отрезкам
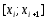 ,
имеем
,
имеем
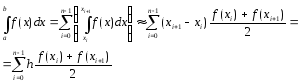 .
.
Полученную
квадратурную ф-лу:
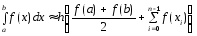 (3)
(3)
называют составной квадратурной формулой трапеций.
Для погрешности составной квадратурной формулы трапеций получаем
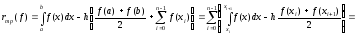
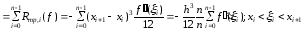 .
.
Т.к.
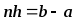 и
и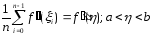 ,
то искомая пог-ть представляется в
виде
,
то искомая пог-ть представляется в
виде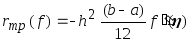 . (4)
. (4)
Применим
теперь при четном n
к интегрированию на частичных отрезках
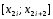 квадратурную формулу парабол. Тогда
квадратурную формулу парабол. Тогда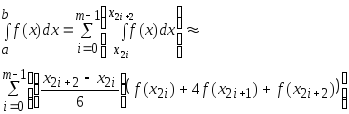 .
Полученную квадратурную формулу
.
Полученную квадратурную формулу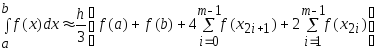 (5)
наз-ют составной квадратурной формулой
парабол (Симпсона).
(5)
наз-ют составной квадратурной формулой
парабол (Симпсона).
Найдем выражение для погрешности расчетной формулы (3).
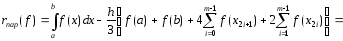
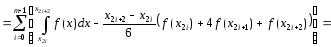
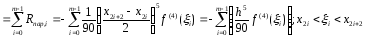 Учитывая,
что
Учитывая,
что
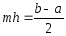 и
и ,
отсюда следует искомое равенство
,
отсюда следует искомое равенство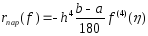 .(6)
.(6)
Как
видно из выражений, полученных для
остаточных членов
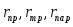 ,
погрешность составных квадратурных
формул можно сделать достаточно малой
за счет выбора меньшего шага сеткиh.
При этом подынтегральная функция должна
быть достаточно гладкой на отрезке
,
погрешность составных квадратурных
формул можно сделать достаточно малой
за счет выбора меньшего шага сеткиh.
При этом подынтегральная функция должна
быть достаточно гладкой на отрезке
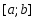 .
.
