
- •1.Источники и классификация погрешностей. Неустранимая и вычислительная погрешность.
- •2. Постановка задачи интерполирования. Существование и единственность обобщенного интерполяционного многочлена.
- •3. Интерполяционный многочлен Лагранжа.
- •4. Схема Эйткина
- •5. Остаточный член интерполяционного многочлена Лагранжа.
- •6. Минимиз. Оценки остаточного члена интерпол. Мн-на.
- •7. Разделенные разности и интерполяционная формула Ньютона с разделенными разностями.
- •8. Конечные разности и интерполяционные формулы Ньютона с конечными разностями.
- •9. Составление таблиц.
- •10. Сходимость интерполяционного процесса
- •11.Общая задача интерполирования алгебраическими многочленами. Интерполяционный многочлен Эрмита с узлами кратности 2.
- •13 . Оптимизация шага при численном диф-нии
- •14. Интерполяционные квадратурные формулы
- •15. Квадратурные формулы Ньютона-Котеса
- •16. Простейшие квадрат ф-лы н-Кот. И оценка их погрешности.
- •17. Составные квадратурные формулы средних прямоугольников, трапеций, парабол и оценка их погрешности
- •18. Квадратурные формулы Гаусса
- •20. Метод наименьших квадратов.
- •22.Обобщённые мног-ны наилучших среднеквадратических приближений.
- •24. Многочлены наилучших равномерных приближений. Примеры.
- •25. Наилучшие приближения в линейном нормированном пространстве.
- •26. Интерполяционные сплайны.
- •27. Существование и единственность кубического сплайна.
- •28.Краткие сведения о нормах векторов и матриц.
- •29. Обусловленность линейных алгебраических систем.
- •30. Метод Гаусса решения системы линейных ур-ний.
- •31. - Разложение квадратных матриц.
- •32. Разложение симметричных матриц. Метод квадр. Корней решения лин. Алг.Систем
- •34. Принцип сжимающих отображений в метрическом пространстве.
- •35. Метод простой итерации решения лин. Алг. Систем и усл. Его сходимости.
- •36. Метод Якоби решения линейных алгебраических систем
- •37. Метод Зейделя решения лин. Алг. Систем.
- •38. Метод покоординатного спуска решения линейных алгебраических систем.
- •39. Метод скорейшего спуска решения линейных алгебраических систем
- •40. Степенной метод решения частичной проблемы собственных значений.
- •41. Метод Данилевского раскрытия характеристического уравнения
- •42. Метод вращений решения полной проблемы собственных значений.
- •43. Метод бисекции и простой итерации решения уравнений с одним неизвестным.
- •44. Методы хорд и касательных как частные случаи метода простой итерации.
- •45. Методы локализации корней алгебраического уравнения.
- •46. Метод Лобачевского решения алгебраических уравнений.
- •47. Методы простой итерации и Зейделя решения системы нелинейных уравнений.
- •48. Метод Ньютона и аналоги метода Зейделя решения системы нелинейных уравнений.
- •49. Классификация численных методов решения задачи Коши. Методы Эйлера, трапеций и к-э.
- •50. Метод Рунге-Кутта решения задачи Коши. Построение методов р-к второго порядка точности.
- •51. Оценка погрешности и сходимость одношаговых методов решения задачи Коши.
- •52. Экстраполяц. Метод Адамса решения задачи Коши.
- •53. Интерполяционный метод Адамса решения задачи Коши.
- •54. Общий вид линейных многошаговых методов решения задачи Коши.
- •55. Условие корней многошаговых методов решения задачи Коши
- •56. Сходимость многошаговых методов решения Коши.
- •57. Сеточные методы решения краевых задач для обыкновенных дифференциальных уравнений.
- •58. Сходимость сеточного метода решения краевых задач для обыкновенных диф. Уравнений.
- •59. Методы прогонки и пристрелки решения разностных схем при решении краевых задач для обыкновенных д.У.
- •60. Эквивалентность граничных и вариационных задач
- •61. Метод Ритца решения вариационных задач.
- •62. Построение системы линейных уравнений для определения значений параметров в методе Ритца.
- •63. Вариационно-разностный вариант метода Рица.
- •64. Сеточные методы решения краевой задачи для уравнения Пуассона. Фоpмулиpовка исходной диффеpенциальной краевой задачи
- •Постpоение pазностной схемы
- •65. Основные понятия теории разностных схем.
- •66. Сходимость сеточного метода
- •Фоpмулиpовка исходной дифференциальной краевой задачи
- •67.Метод матричной прогонки решения разностной схемы. Фоpмулиpовка исходной диффеpенциальной краевой задачи
- •68. Разностные схемы для одномерного параболического уравнения. Фоpмулиpовка исходной диффеpенциальной задачи
- •69. Разностные схемы решения задачи Коши для уравнения гиперболического типа.
- •70. Сеточные методы решения смешанной задачи для уравнений гиперболического типа.
- •71. Метод квадратур решения интегрального уравнения Фредгольма 2-го рода.
- •72. Решение интегрального уравнения Фредгольма 2-го рода с вырожденным ядром.
- •Решение интегр. Ур-ния с вырожденным ядром.
- •73. Решение интегрального уравнения Фредгольма 2-го рода методом вырожденного ядра.
- •Способы приближения невырожденного ядра вырожденным.
42. Метод вращений решения полной проблемы собственных значений.
Метод
вращений предназначен для решения
полной проблемы собственных значений
для эрмитовых матриц. В алгебре
доказывается, что для эрмитовой матрицы
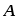 существует унитарная матрица
существует унитарная матрица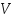 ,
такая, что преобразование подобия с ней
приводит матрицу
,
такая, что преобразование подобия с ней
приводит матрицу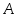 к диагональной матрице
к диагональной матрице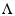 :
: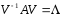 (1)
(1)
Для
унитарной матрицы по определению
сопряженная матрица равна обратной:
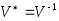 .
Таким образом, равенство (1) можно
переписать в виде
.
Таким образом, равенство (1) можно
переписать в виде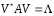 (2)
(2)
Собственными
значениями диагональной матрицы
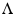 являются ее диагональные элементы
являются ее диагональные элементы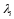 ,
а собственными векторами - соответствующие
единичные (координатные) векторы
,
а собственными векторами - соответствующие
единичные (координатные) векторы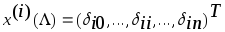 ,
где
,
где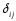 - символ Кронекера. Выполнение равенств
- символ Кронекера. Выполнение равенств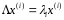 в данном случае очевидно.
в данном случае очевидно.
Строки
унитарной матрицы
 являются собственными векторами матрицы
являются собственными векторами матрицы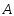 .
Это следует из(2):
.
Это следует из(2):
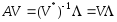 .
Действительно, отсюда имеем
.
Действительно, отсюда имеем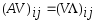 или
или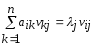 или
или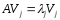 ,
где
,
где .
.
Вещественные симметрические матрицы являются частным случаем эрмитовых матриц. Рассмотрим метод вращений для вещественных симметрических матриц.
Найдем
наибольший по модулю внедиагональный
элемент вещественной симметрической
матрицы
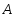 .
Пусть таковым оказался элемент
.
Пусть таковым оказался элемент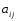 .Без
ограничения общности можно считать
.Без
ограничения общности можно считать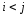 .
.
Введем в рассмотрение матрицу вращения

Умножим
матрицу
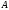 справа на матрицу
справа на матрицу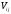 .
Получим матрицу
.
Получим матрицу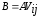 ,
которая отличается от матрицы
,
которая отличается от матрицы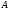 только столбцамиi
и j:
только столбцамиi
и j:
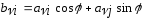 (3),
(3),
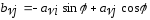 (4)
(4)
Из (3) и (4) при этом следует, что сумма квадратов элементов этих столбцов остается без изменения:
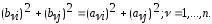 (5)
(5)
Умножим
матрицу
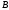 слева на матрицу
слева на матрицу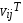 .
Получим матрицу
.
Получим матрицу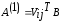 ,
которая отличается от матрицы
,
которая отличается от матрицы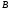 только строкамиi
и j:
только строкамиi
и j:
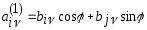 (6),
(6),
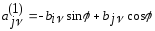 (7)
(7)
Из (6) и (7) при этом следует, что сумма квадратов элементов этих строк остается без изменения:
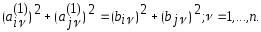 (8)
(8)
Таким образом, преобразование подобия
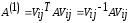 (9)
не меняет суммы квадратов элементов
матрицы:
(9)
не меняет суммы квадратов элементов
матрицы: 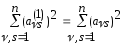
Преобразование
подобия (9) также сохраняет симметричность
матрицы:
 .
.
Теперь
начинается самое главное. Преобразование
подобия (9) меняет только два диагональных
элемента. При этом, из симметрии , формул
(8) и (5) следует:
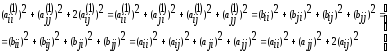 Это
значит, что при
Это
значит, что при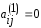 преобразование (9) увеличит сумму
квадратов диагональных элементов и
соответственно уменьшит сумму квадратов
внедиагональных элементов матрицы на
величину
преобразование (9) увеличит сумму
квадратов диагональных элементов и
соответственно уменьшит сумму квадратов
внедиагональных элементов матрицы на
величину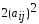 .
Из (6) и (4) получаем уравнение для
определения соответствующего угла
.
Из (6) и (4) получаем уравнение для
определения соответствующего угла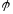
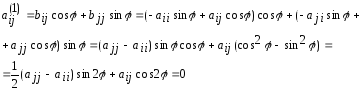
Отсюда
находим искомый угол поворота
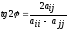 ,
,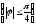 (10)
(10)
Мы
рассмотрели идею метода вращений и
получили расчетные формулы метода. В
методе вращений строится последовательность
матриц
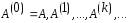 (11)
(11)
по
правилу
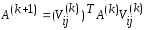 (12)
(12)
Построение
последовательности (11) заканчивается
получением матрицы
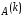 ,
недиагональные элементы которой можно
считать равными нулю в пределах заданной
точности. При этом ее диагональные
элементы принимаются за собственные
значения.
,
недиагональные элементы которой можно
считать равными нулю в пределах заданной
точности. При этом ее диагональные
элементы принимаются за собственные
значения.
В
качестве собственных векторов можно
взять соответствующие строки матрицы
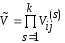 .
Может оказаться, что собственные векторы
проще находить непосредственно решением
систем
.
Может оказаться, что собственные векторы
проще находить непосредственно решением
систем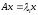 .
.
Теорема. Матричная последовательность (11) в методе вращений сходится к диагональной матрице со скоростью геометрической погрешности.
Доказательство.
Обозначим
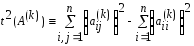 .
Имеем
.
Имеем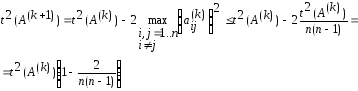 .
Следовательно, сумма квадратов
недиагональных элементов в матричной
последовательности (11) сходится к нулю
не хуже, чем геометрическая последовательность
со знаменателем
.
Следовательно, сумма квадратов
недиагональных элементов в матричной
последовательности (11) сходится к нулю
не хуже, чем геометрическая последовательность
со знаменателем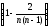 .
Теорема доказана.
.
Теорема доказана.
