
- •1.Источники и классификация погрешностей. Неустранимая и вычислительная погрешность.
- •2. Постановка задачи интерполирования. Существование и единственность обобщенного интерполяционного многочлена.
- •3. Интерполяционный многочлен Лагранжа.
- •4. Схема Эйткина
- •5. Остаточный член интерполяционного многочлена Лагранжа.
- •6. Минимиз. Оценки остаточного члена интерпол. Мн-на.
- •7. Разделенные разности и интерполяционная формула Ньютона с разделенными разностями.
- •8. Конечные разности и интерполяционные формулы Ньютона с конечными разностями.
- •9. Составление таблиц.
- •10. Сходимость интерполяционного процесса
- •11.Общая задача интерполирования алгебраическими многочленами. Интерполяционный многочлен Эрмита с узлами кратности 2.
- •13 . Оптимизация шага при численном диф-нии
- •14. Интерполяционные квадратурные формулы
- •15. Квадратурные формулы Ньютона-Котеса
- •16. Простейшие квадрат ф-лы н-Кот. И оценка их погрешности.
- •17. Составные квадратурные формулы средних прямоугольников, трапеций, парабол и оценка их погрешности
- •18. Квадратурные формулы Гаусса
- •20. Метод наименьших квадратов.
- •22.Обобщённые мног-ны наилучших среднеквадратических приближений.
- •24. Многочлены наилучших равномерных приближений. Примеры.
- •25. Наилучшие приближения в линейном нормированном пространстве.
- •26. Интерполяционные сплайны.
- •27. Существование и единственность кубического сплайна.
- •28.Краткие сведения о нормах векторов и матриц.
- •29. Обусловленность линейных алгебраических систем.
- •30. Метод Гаусса решения системы линейных ур-ний.
- •31. - Разложение квадратных матриц.
- •32. Разложение симметричных матриц. Метод квадр. Корней решения лин. Алг.Систем
- •34. Принцип сжимающих отображений в метрическом пространстве.
- •35. Метод простой итерации решения лин. Алг. Систем и усл. Его сходимости.
- •36. Метод Якоби решения линейных алгебраических систем
- •37. Метод Зейделя решения лин. Алг. Систем.
- •38. Метод покоординатного спуска решения линейных алгебраических систем.
- •39. Метод скорейшего спуска решения линейных алгебраических систем
- •40. Степенной метод решения частичной проблемы собственных значений.
- •41. Метод Данилевского раскрытия характеристического уравнения
- •42. Метод вращений решения полной проблемы собственных значений.
- •43. Метод бисекции и простой итерации решения уравнений с одним неизвестным.
- •44. Методы хорд и касательных как частные случаи метода простой итерации.
- •45. Методы локализации корней алгебраического уравнения.
- •46. Метод Лобачевского решения алгебраических уравнений.
- •47. Методы простой итерации и Зейделя решения системы нелинейных уравнений.
- •48. Метод Ньютона и аналоги метода Зейделя решения системы нелинейных уравнений.
- •49. Классификация численных методов решения задачи Коши. Методы Эйлера, трапеций и к-э.
- •50. Метод Рунге-Кутта решения задачи Коши. Построение методов р-к второго порядка точности.
- •51. Оценка погрешности и сходимость одношаговых методов решения задачи Коши.
- •52. Экстраполяц. Метод Адамса решения задачи Коши.
- •53. Интерполяционный метод Адамса решения задачи Коши.
- •54. Общий вид линейных многошаговых методов решения задачи Коши.
- •55. Условие корней многошаговых методов решения задачи Коши
- •56. Сходимость многошаговых методов решения Коши.
- •57. Сеточные методы решения краевых задач для обыкновенных дифференциальных уравнений.
- •58. Сходимость сеточного метода решения краевых задач для обыкновенных диф. Уравнений.
- •59. Методы прогонки и пристрелки решения разностных схем при решении краевых задач для обыкновенных д.У.
- •60. Эквивалентность граничных и вариационных задач
- •61. Метод Ритца решения вариационных задач.
- •62. Построение системы линейных уравнений для определения значений параметров в методе Ритца.
- •63. Вариационно-разностный вариант метода Рица.
- •64. Сеточные методы решения краевой задачи для уравнения Пуассона. Фоpмулиpовка исходной диффеpенциальной краевой задачи
- •Постpоение pазностной схемы
- •65. Основные понятия теории разностных схем.
- •66. Сходимость сеточного метода
- •Фоpмулиpовка исходной дифференциальной краевой задачи
- •67.Метод матричной прогонки решения разностной схемы. Фоpмулиpовка исходной диффеpенциальной краевой задачи
- •68. Разностные схемы для одномерного параболического уравнения. Фоpмулиpовка исходной диффеpенциальной задачи
- •69. Разностные схемы решения задачи Коши для уравнения гиперболического типа.
- •70. Сеточные методы решения смешанной задачи для уравнений гиперболического типа.
- •71. Метод квадратур решения интегрального уравнения Фредгольма 2-го рода.
- •72. Решение интегрального уравнения Фредгольма 2-го рода с вырожденным ядром.
- •Решение интегр. Ур-ния с вырожденным ядром.
- •73. Решение интегрального уравнения Фредгольма 2-го рода методом вырожденного ядра.
- •Способы приближения невырожденного ядра вырожденным.
20. Метод наименьших квадратов.
Пусть ф-ия f(x) задана табл. yi=f(xi); i=0,…n. Надо эту ф-ию приблизить ф-ей вида φ(x, a0,...,am). Знач-я неизвест-х парам-ов aj;j=0,...m надо выбрать т.ч. сумма кв-ов отклонений
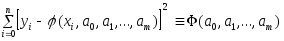 (1)
ф-ии f
от ф-ии φ
по всем табл-ым узлам xi
была мин-ой. Е. ф-ия φ
явл. достаточно гладкой, то искомые зн.
параметров м.б. найдены из условий Ферма
(1)
ф-ии f
от ф-ии φ
по всем табл-ым узлам xi
была мин-ой. Е. ф-ия φ
явл. достаточно гладкой, то искомые зн.
параметров м.б. найдены из условий Ферма
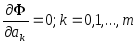 .
(2)
.
(2)
Когда ф-ия φ
линейно зависит от параметров:
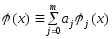 ,
с-ма (2) будет линейной
,
с-ма (2) будет линейной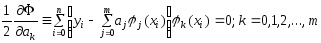 .
После простых преобразований с-ма:
.
После простых преобразований с-ма:
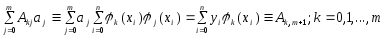 .(3)
.(3)
Определитель
 с-мы - определитель Грама с элементамиAkj,
равными скалярным произвед-ям
с-мы - определитель Грама с элементамиAkj,
равными скалярным произвед-ям
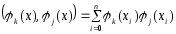 .
.
Теорема.
Если последов-ть непрерывных ф-ций
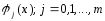 явл. сис-мой Чебышева на [a;b],
то определитель с-мы (3) ≠ 0 при любых
наборах попарно неравных узлов
явл. сис-мой Чебышева на [a;b],
то определитель с-мы (3) ≠ 0 при любых
наборах попарно неравных узлов
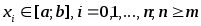 .
.
Доказательство.
Противное: последов-сть ф-ий явл. сис-мой
Чебышева на отр-е, но
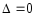 при некот-ом наборе попарно неравных
узлов. Тогда столбцы определителя будут
линейно зависимыми
при некот-ом наборе попарно неравных
узлов. Тогда столбцы определителя будут
линейно зависимыми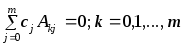 .
=>
.
=>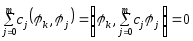 .
Умножая последние равенства на
соответствующиеck
и проводя суммирование по k,
получим
.
Умножая последние равенства на
соответствующиеck
и проводя суммирование по k,
получим
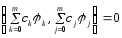 ,
откуда
,
откуда
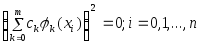 .
Т. о., нетривиальный обобщенный многочлен
.
Т. о., нетривиальный обобщенный многочлен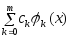 обращается в 0 на отрезке не менее чем
вn+1-й
точке, что > m.
Полученное противоречие доказывает
теорему.
обращается в 0 на отрезке не менее чем
вn+1-й
точке, что > m.
Полученное противоречие доказывает
теорему.
При m=n единственным решение – интерполяц-ый обобщенный многочлен φ(x); при этом min сумма квадратов отклонений: Ф=0.
Сис-ма ф-ий
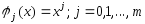 явл. сис-мой Чебышева на любом отр.,
поэтому наилучшее приближение табличной
ф-ииyi=f(xi)
алгебраическим многочленом
явл. сис-мой Чебышева на любом отр.,
поэтому наилучшее приближение табличной
ф-ииyi=f(xi)
алгебраическим многочленом
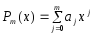 степениm<=n
по методу наименьших квадратов сущ-ет,
явл. единственным и коэффиценты многочлена
м.б. найдены из линейной алгебраической
системы
степениm<=n
по методу наименьших квадратов сущ-ет,
явл. единственным и коэффиценты многочлена
м.б. найдены из линейной алгебраической
системы
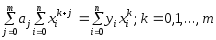 .
Приm=2
система:
.
Приm=2
система:
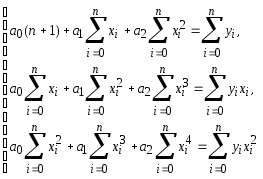
22.Обобщённые мног-ны наилучших среднеквадратических приближений.
Будем
апроксим. ф-ию f(x)
некот. ф-ей
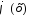 т.о.
, чтобы ф-ия
т.о.
, чтобы ф-ия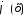 в
среднем достаточно хорошо описывала
поведение ф-ииf
.Будем считать , что ф-ии f
и
в
среднем достаточно хорошо описывала
поведение ф-ииf
.Будем считать , что ф-ии f
и
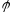 непрерывны
на
непрерывны
на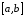 .
Одновременно будем рассм. Два случая:
.
Одновременно будем рассм. Два случая:
1)
f
и
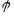 непрерывны
на
непрерывны
на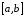 и близость между ф-ямиf
и
и близость между ф-ямиf
и
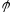 понимается
в интегральном смысле.
понимается
в интегральном смысле.
2)
f
и
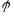 заданы
только в точках
заданы
только в точках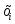 ,
,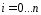 отрезка
отрезка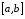 в
которых производится согласование
между этими ф-ями.
в
которых производится согласование
между этими ф-ями.
Двум случаям поставим в соответствие непрерывное и дискретное пр-во.
1)
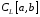 -
пр-во непрерывных на
-
пр-во непрерывных на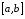 ф-ий с метрикой
ф-ий с метрикой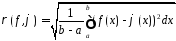 .
.
Скалярное произведение равно:
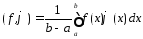 и нормой
и нормой
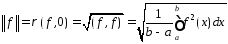 .
.
2)
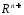 про-во
сеточных ф-ийf(x),
т.е. опред. В узлах сетки
про-во
сеточных ф-ийf(x),
т.е. опред. В узлах сетки
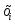 принадлежит
принадлежит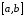 с
метрикой
с
метрикой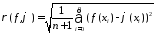
Скалярное произведение равно:
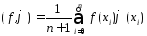 и нормой
и нормой
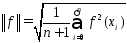
Введём
в пр-вах
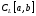 и
и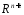 метрики
по отношению приближённому равенству
метрики
по отношению приближённому равенству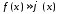 предстовл.
собой интегральную и дискретную
(точечную) средне квадратические ошибки.
Пусть ф-ия
предстовл.
собой интегральную и дискретную
(точечную) средне квадратические ошибки.
Пусть ф-ия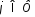 ,
гдеФ
некоторое множество ф-ий. В соответствии
с методом наименьших квадратов(МНК)
имеем зад. опред. ф-ии
,
гдеФ
некоторое множество ф-ий. В соответствии
с методом наименьших квадратов(МНК)
имеем зад. опред. ф-ии
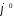 такой,
что
такой,
что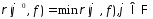 (1).
(1).
Решив задачу (1) получим наилучшее среднеквадратическое приближение для ф-ии f.
Предположим,
что
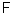 есть
некоторое подпространство натянутых
на ф-ию
есть
некоторое подпространство натянутых
на ф-ию ,
тогда несложно заметить, что решением
(1) будет ф-ия
,
тогда несложно заметить, что решением
(1) будет ф-ия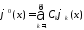 ,
где коэффиц.
,
где коэффиц.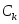 удовлетворяет
системе алг. ур.:
удовлетворяет
системе алг. ур.: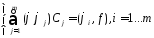 (2)
(2)
Рассмотрим
матрицу
 ,
которая наз. матрицей Грамма.
,
которая наз. матрицей Грамма.
Лемма:
Если ф-ия
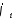 -
лин. незав., то матрица G – положительно
определённая.
-
лин. незав., то матрица G – положительно
определённая.
Д-во:Имеем
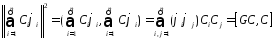 ,
,
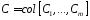 ,
а
,
а
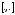 - скалярное произведение в
- скалярное произведение в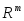 .
.
Поскольку
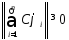 ,
причём знак рав-ва имеет место только
в случае
,
причём знак рав-ва имеет место только
в случае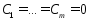 ,
то кв. ф.
,
то кв. ф.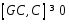 .
Т.о. система (2) однозначно разрешима. Из
системы (2) находим коэфф.
.
Т.о. система (2) однозначно разрешима. Из
системы (2) находим коэфф. и многочлен
и многочлен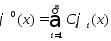 ,
который называется многочленом наилучшего
среднеквадратического приближения.
,
который называется многочленом наилучшего
среднеквадратического приближения.
Наибольший интерес
преедстовляет случай , когда ф-ия
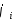 - ортогональны, в этом случае матрицаG
имеет вид
- ортогональны, в этом случае матрицаG
имеет вид
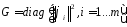 b
решение (2) определяется формулой
b
решение (2) определяется формулой
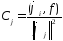 .
В этом случаеG-
наз. коэффиц. Фурье, а многочлен
.
В этом случаеG-
наз. коэффиц. Фурье, а многочлен
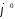 -
обобщенным многочленом Фурье. Если ф-ия
-
обобщенным многочленом Фурье. Если ф-ия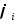 - ортонормированны, то обобщенный
многочлен Фурье имеет вид:
- ортонормированны, то обобщенный
многочлен Фурье имеет вид: .
.
