
- •1.Источники и классификация погрешностей. Неустранимая и вычислительная погрешность.
- •2. Постановка задачи интерполирования. Существование и единственность обобщенного интерполяционного многочлена.
- •3. Интерполяционный многочлен Лагранжа.
- •4. Схема Эйткина
- •5. Остаточный член интерполяционного многочлена Лагранжа.
- •6. Минимиз. Оценки остаточного члена интерпол. Мн-на.
- •7. Разделенные разности и интерполяционная формула Ньютона с разделенными разностями.
- •8. Конечные разности и интерполяционные формулы Ньютона с конечными разностями.
- •9. Составление таблиц.
- •10. Сходимость интерполяционного процесса
- •11.Общая задача интерполирования алгебраическими многочленами. Интерполяционный многочлен Эрмита с узлами кратности 2.
- •13 . Оптимизация шага при численном диф-нии
- •14. Интерполяционные квадратурные формулы
- •15. Квадратурные формулы Ньютона-Котеса
- •16. Простейшие квадрат ф-лы н-Кот. И оценка их погрешности.
- •17. Составные квадратурные формулы средних прямоугольников, трапеций, парабол и оценка их погрешности
- •18. Квадратурные формулы Гаусса
- •20. Метод наименьших квадратов.
- •22.Обобщённые мног-ны наилучших среднеквадратических приближений.
- •24. Многочлены наилучших равномерных приближений. Примеры.
- •25. Наилучшие приближения в линейном нормированном пространстве.
- •26. Интерполяционные сплайны.
- •27. Существование и единственность кубического сплайна.
- •28.Краткие сведения о нормах векторов и матриц.
- •29. Обусловленность линейных алгебраических систем.
- •30. Метод Гаусса решения системы линейных ур-ний.
- •31. - Разложение квадратных матриц.
- •32. Разложение симметричных матриц. Метод квадр. Корней решения лин. Алг.Систем
- •34. Принцип сжимающих отображений в метрическом пространстве.
- •35. Метод простой итерации решения лин. Алг. Систем и усл. Его сходимости.
- •36. Метод Якоби решения линейных алгебраических систем
- •37. Метод Зейделя решения лин. Алг. Систем.
- •38. Метод покоординатного спуска решения линейных алгебраических систем.
- •39. Метод скорейшего спуска решения линейных алгебраических систем
- •40. Степенной метод решения частичной проблемы собственных значений.
- •41. Метод Данилевского раскрытия характеристического уравнения
- •42. Метод вращений решения полной проблемы собственных значений.
- •43. Метод бисекции и простой итерации решения уравнений с одним неизвестным.
- •44. Методы хорд и касательных как частные случаи метода простой итерации.
- •45. Методы локализации корней алгебраического уравнения.
- •46. Метод Лобачевского решения алгебраических уравнений.
- •47. Методы простой итерации и Зейделя решения системы нелинейных уравнений.
- •48. Метод Ньютона и аналоги метода Зейделя решения системы нелинейных уравнений.
- •49. Классификация численных методов решения задачи Коши. Методы Эйлера, трапеций и к-э.
- •50. Метод Рунге-Кутта решения задачи Коши. Построение методов р-к второго порядка точности.
- •51. Оценка погрешности и сходимость одношаговых методов решения задачи Коши.
- •52. Экстраполяц. Метод Адамса решения задачи Коши.
- •53. Интерполяционный метод Адамса решения задачи Коши.
- •54. Общий вид линейных многошаговых методов решения задачи Коши.
- •55. Условие корней многошаговых методов решения задачи Коши
- •56. Сходимость многошаговых методов решения Коши.
- •57. Сеточные методы решения краевых задач для обыкновенных дифференциальных уравнений.
- •58. Сходимость сеточного метода решения краевых задач для обыкновенных диф. Уравнений.
- •59. Методы прогонки и пристрелки решения разностных схем при решении краевых задач для обыкновенных д.У.
- •60. Эквивалентность граничных и вариационных задач
- •61. Метод Ритца решения вариационных задач.
- •62. Построение системы линейных уравнений для определения значений параметров в методе Ритца.
- •63. Вариационно-разностный вариант метода Рица.
- •64. Сеточные методы решения краевой задачи для уравнения Пуассона. Фоpмулиpовка исходной диффеpенциальной краевой задачи
- •Постpоение pазностной схемы
- •65. Основные понятия теории разностных схем.
- •66. Сходимость сеточного метода
- •Фоpмулиpовка исходной дифференциальной краевой задачи
- •67.Метод матричной прогонки решения разностной схемы. Фоpмулиpовка исходной диффеpенциальной краевой задачи
- •68. Разностные схемы для одномерного параболического уравнения. Фоpмулиpовка исходной диффеpенциальной задачи
- •69. Разностные схемы решения задачи Коши для уравнения гиперболического типа.
- •70. Сеточные методы решения смешанной задачи для уравнений гиперболического типа.
- •71. Метод квадратур решения интегрального уравнения Фредгольма 2-го рода.
- •72. Решение интегрального уравнения Фредгольма 2-го рода с вырожденным ядром.
- •Решение интегр. Ур-ния с вырожденным ядром.
- •73. Решение интегрального уравнения Фредгольма 2-го рода методом вырожденного ядра.
- •Способы приближения невырожденного ядра вырожденным.
48. Метод Ньютона и аналоги метода Зейделя решения системы нелинейных уравнений.
Рассмотрим систему
нелинейных уравнений, заданную в виде
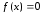 , (4),
где
, (4),
где –n-вектор-функция,
заданная в n-мерном
векторном пространстве или на некотором
его множестве. Пусть система (4) имеет
решение
–n-вектор-функция,
заданная в n-мерном
векторном пространстве или на некотором
его множестве. Пусть система (4) имеет
решение
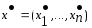 и Якобиан
и Якобиан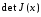 ,
где
,
где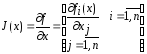 - матрица Якоби вектор-функции
- матрица Якоби вектор-функции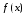 ,
отличен от нуля в области
,
отличен от нуля в области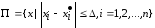 .
Тогда нелинейная система
.
Тогда нелинейная система
 (5)
равносильна в области П системе (4).
Примененный к решению системы (5) метод
простой итерации
(5)
равносильна в области П системе (4).
Примененный к решению системы (5) метод
простой итерации
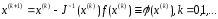 (6)
называют методом Ньютона для решения
системы (4).
(6)
называют методом Ньютона для решения
системы (4).
Найдем значения
частных производных
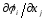 в точке
в точке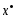 :
:
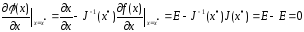 .
.
В силу непрерывности
рассматриваемых функций и их производных
существует достаточно малое
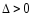 ,
что в П будут выполнены условия
,
что в П будут выполнены условия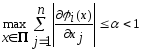 .
Таким образом, метод Ньютона (6) будет
сходиться при любом начальном приближении
из П.
.
Таким образом, метод Ньютона (6) будет
сходиться при любом начальном приближении
из П.
Покажем, что метод Ньютона (6) имеет квадратический характер сходимости. При этом воспользуемся разложением в ряд Тэйлора:
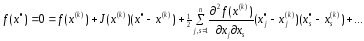 (7)
Воспользуемся формулой (6) и разложением
(7):
(7)
Воспользуемся формулой (6) и разложением
(7):
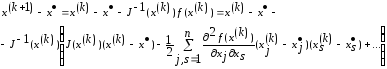 Отсюда
получаем искомую приближенную оценку
Отсюда
получаем искомую приближенную оценку
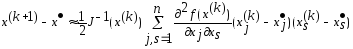
Для решения системы
в виде (4) применяются различные аналоги
метода Зейделя. Рассмотрим один из них.
Пусть уже найдено приближение
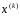 .
Вычислим невязки:
.
Вычислим невязки:
 .
Найдем наибольшую по модулю невязку.
Пусть таковой оказалась невязка
.
Найдем наибольшую по модулю невязку.
Пусть таковой оказалась невязка
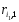 .
Далее решаем уравнение
.
Далее решаем уравнение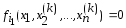 относительно неизвестной
относительно неизвестной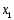 .
Найденное решение принимают за
.
Найденное решение принимают за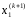 .
Затем вычислим невязки
.
Затем вычислим невязки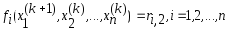 .Выберем
наибольшую по модулю невязку
.Выберем
наибольшую по модулю невязку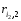 ,
решим уравнение
,
решим уравнение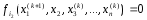 относительно
относительно и получим приближение
и получим приближение .
Далее выполняются аналогичные действия,
пока не будут найдены все компоненты
для приближения
.
Далее выполняются аналогичные действия,
пока не будут найдены все компоненты
для приближения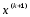 .
Потом увеличивается значениеk
на единицу и процесс повторяется.
Вычисления прекращаются, когда невязки
по модуля станут достаточно малыми.
.
Потом увеличивается значениеk
на единицу и процесс повторяется.
Вычисления прекращаются, когда невязки
по модуля станут достаточно малыми.
49. Классификация численных методов решения задачи Коши. Методы Эйлера, трапеций и к-э.
Рассмотрим на
отрезке
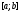 задачу Коши для нелинейного обыкновенного
дифференциального уравнения первого
порядка
задачу Коши для нелинейного обыкновенного
дифференциального уравнения первого
порядка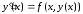 (1) с начальным условием
(1) с начальным условием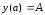 .(2)
.(2)
Пусть задача Коши
(1), (2) имеет единственное решение
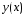 .
На отрезке
.
На отрезке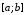 зададим последовательность точек
зададим последовательность точек
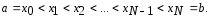 (3)
(3)
Говорят, что на
отрезке введена сетка. Сетка – это
конечное множество точек, в данном
случае, на отрезке. Точки
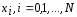 называют узлами сетки. Узлы
называют узлами сетки. Узлы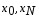 называют граничными, остальные узлы
сетки – внутренними. Если расстояние
называют граничными, остальные узлы
сетки – внутренними. Если расстояние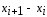 между соседними узлами сетки не одинаково,
то говорят, что задана неравномерная
сетка. Если же
между соседними узлами сетки не одинаково,
то говорят, что задана неравномерная
сетка. Если же ,
то говорят, что на отрезке задана
равномерная сетка с шагом
,
то говорят, что на отрезке задана
равномерная сетка с шагом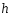 .
В численных методах решения задачи Коши
приближенное решение ищется в виде
таблицы чисел
.
В численных методах решения задачи Коши
приближенное решение ищется в виде
таблицы чисел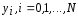 ,
приближающих значения
,
приближающих значения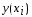 точного решения в узлах сетки. Расчетные
формулы численных методов решения
задачи Коши в большинстве случаев можно
представить в виде
точного решения в узлах сетки. Расчетные
формулы численных методов решения
задачи Коши в большинстве случаев можно
представить в виде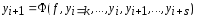 . (4)
Здесь функция
. (4)
Здесь функция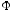 опр-ся выбором сетки и способом построения
метода. Если
опр-ся выбором сетки и способом построения
метода. Если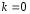 ,
,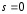 ,
то расчетная формула (4) принимает вид
,
то расчетная формула (4) принимает вид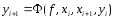 . (5).
Такие методы называют явными одношаговыми.
Если
. (5).
Такие методы называют явными одношаговыми.
Если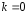 ,
,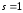 ,
то расчетная формула (4) принимает вид
,
то расчетная формула (4) принимает вид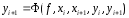 . (6).
Соотв-ий метод называют неявным
одношаговым. В случае когда в расчетной
формуле (4)
. (6).
Соотв-ий метод называют неявным
одношаговым. В случае когда в расчетной
формуле (4) или
или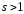 ,
методы называют многошаговыми. При
,
методы называют многошаговыми. При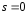 многошаговые методы, как и одношаговые,
называются явными, а при
многошаговые методы, как и одношаговые,
называются явными, а при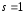 - неявными.
- неявными.
Методы Эйлера, трапеций и Коши-Эйлера.
Рассмотрим задачу
Коши для нелинейного о. д. у. первого
порядка:
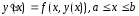 , (7)
, (7)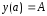 . (8)
. (8)
На отрезке
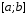 введем сетку
введем сетку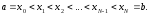 (9)
(9)
Геометр. вывод расчетной формулы метода Эйлера.
Пусть найдено уже
приближение
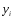 к решению
к решению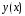 задачи (7), (8) в узле
задачи (7), (8) в узле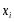 сетки (9). Обозначим через
сетки (9). Обозначим через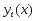 интегральную кривую дифференциального
уравнения (7), проходящую через точку
интегральную кривую дифференциального
уравнения (7), проходящую через точку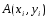 .
Проведем к этой интегральной кривой
касательную в точке
.
Проведем к этой интегральной кривой
касательную в точке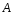 до пересечения с вертикалью
до пересечения с вертикалью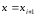 в точке
в точке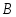 и
ординату точки
и
ординату точки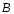 возьмем в качестве приближения
возьмем в качестве приближения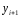 к решению
к решению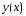 задачи (7), (8) в узле
задачи (7), (8) в узле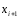 .
.
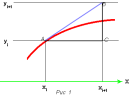
Из прямоугольного
треугольника
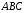 найдем выражение для вычисления
найдем выражение для вычисления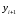
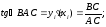
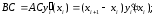
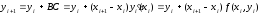 .
.
Получили для
решения задачи Коши (7), (8) расчетную
формулу метода Эйлера:
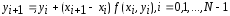 (10)
(10)
Аналитич. вывод расчетной формулы метода Эйлера.
Проведем разложение в ряд Тейлора (11)
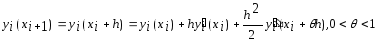
Из
этого разложения с учетом, что
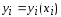 и
и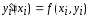 ,
получаем снова расчетное правило метода
Эйлера
,
получаем снова расчетное правило метода
Эйлера . (10)
. (10)
Метод Эйлера
является одношаговым и явным. Из формул
(10) и (11) для погрешности
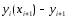 метода Эйлера на шаге следует оценка
метода Эйлера на шаге следует оценка
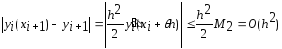 , (11)
, (11)
где
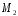 -
максимальное значение вторых производных
для интегральных кривых, лежащих в
рассматриваемой окрестности решения
-
максимальное значение вторых производных
для интегральных кривых, лежащих в
рассматриваемой окрестности решения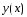 .
.
Погрешность
одношагового метода
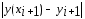 есть величина на единицу меньшего
порядка относительно
есть величина на единицу меньшего
порядка относительно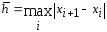 по сравнению с погрешностью на шаге
(11). Таким образом, метод Эйлера относится
к численным методам первого порядка
точности.
по сравнению с погрешностью на шаге
(11). Таким образом, метод Эйлера относится
к численным методам первого порядка
точности.
Использование квадратурных формул для построения численных методов решения задачи Коши.
Расчетную формулу
(10) метода Эйлера можно получить также,
применяя квадратурную формулу левых
прямоугольников к интегралу в формуле
Ньютона-Лейбница
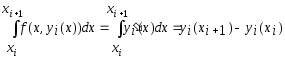 . (12)
. (12)
Если применить к
вычислению интеграла в (10) квадратурную
формулу трапеций, то получим расчетное
правило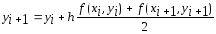 (13)
неявного метода Адамса второго порядка
точности или метода трапеций.
(13)
неявного метода Адамса второго порядка
точности или метода трапеций.
Расчетная формула
(11) представляет собой уравнение с одним
неизвестным
 .
Если начальное приближение вычислить
по методу Эйлера и сделать одну итерацию
при решении уравнения (13), то получим
расчетную формулу
.
Если начальное приближение вычислить
по методу Эйлера и сделать одну итерацию
при решении уравнения (13), то получим
расчетную формулу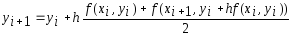 (8)
(8)
метода Коши-Эйлера. Это явный метод второго порядка точности.
