
- •1.Источники и классификация погрешностей. Неустранимая и вычислительная погрешность.
- •2. Постановка задачи интерполирования. Существование и единственность обобщенного интерполяционного многочлена.
- •3. Интерполяционный многочлен Лагранжа.
- •4. Схема Эйткина
- •5. Остаточный член интерполяционного многочлена Лагранжа.
- •6. Минимиз. Оценки остаточного члена интерпол. Мн-на.
- •7. Разделенные разности и интерполяционная формула Ньютона с разделенными разностями.
- •8. Конечные разности и интерполяционные формулы Ньютона с конечными разностями.
- •9. Составление таблиц.
- •10. Сходимость интерполяционного процесса
- •11.Общая задача интерполирования алгебраическими многочленами. Интерполяционный многочлен Эрмита с узлами кратности 2.
- •13 . Оптимизация шага при численном диф-нии
- •14. Интерполяционные квадратурные формулы
- •15. Квадратурные формулы Ньютона-Котеса
- •16. Простейшие квадрат ф-лы н-Кот. И оценка их погрешности.
- •17. Составные квадратурные формулы средних прямоугольников, трапеций, парабол и оценка их погрешности
- •18. Квадратурные формулы Гаусса
- •20. Метод наименьших квадратов.
- •22.Обобщённые мног-ны наилучших среднеквадратических приближений.
- •24. Многочлены наилучших равномерных приближений. Примеры.
- •25. Наилучшие приближения в линейном нормированном пространстве.
- •26. Интерполяционные сплайны.
- •27. Существование и единственность кубического сплайна.
- •28.Краткие сведения о нормах векторов и матриц.
- •29. Обусловленность линейных алгебраических систем.
- •30. Метод Гаусса решения системы линейных ур-ний.
- •31. - Разложение квадратных матриц.
- •32. Разложение симметричных матриц. Метод квадр. Корней решения лин. Алг.Систем
- •34. Принцип сжимающих отображений в метрическом пространстве.
- •35. Метод простой итерации решения лин. Алг. Систем и усл. Его сходимости.
- •36. Метод Якоби решения линейных алгебраических систем
- •37. Метод Зейделя решения лин. Алг. Систем.
- •38. Метод покоординатного спуска решения линейных алгебраических систем.
- •39. Метод скорейшего спуска решения линейных алгебраических систем
- •40. Степенной метод решения частичной проблемы собственных значений.
- •41. Метод Данилевского раскрытия характеристического уравнения
- •42. Метод вращений решения полной проблемы собственных значений.
- •43. Метод бисекции и простой итерации решения уравнений с одним неизвестным.
- •44. Методы хорд и касательных как частные случаи метода простой итерации.
- •45. Методы локализации корней алгебраического уравнения.
- •46. Метод Лобачевского решения алгебраических уравнений.
- •47. Методы простой итерации и Зейделя решения системы нелинейных уравнений.
- •48. Метод Ньютона и аналоги метода Зейделя решения системы нелинейных уравнений.
- •49. Классификация численных методов решения задачи Коши. Методы Эйлера, трапеций и к-э.
- •50. Метод Рунге-Кутта решения задачи Коши. Построение методов р-к второго порядка точности.
- •51. Оценка погрешности и сходимость одношаговых методов решения задачи Коши.
- •52. Экстраполяц. Метод Адамса решения задачи Коши.
- •53. Интерполяционный метод Адамса решения задачи Коши.
- •54. Общий вид линейных многошаговых методов решения задачи Коши.
- •55. Условие корней многошаговых методов решения задачи Коши
- •56. Сходимость многошаговых методов решения Коши.
- •57. Сеточные методы решения краевых задач для обыкновенных дифференциальных уравнений.
- •58. Сходимость сеточного метода решения краевых задач для обыкновенных диф. Уравнений.
- •59. Методы прогонки и пристрелки решения разностных схем при решении краевых задач для обыкновенных д.У.
- •60. Эквивалентность граничных и вариационных задач
- •61. Метод Ритца решения вариационных задач.
- •62. Построение системы линейных уравнений для определения значений параметров в методе Ритца.
- •63. Вариационно-разностный вариант метода Рица.
- •64. Сеточные методы решения краевой задачи для уравнения Пуассона. Фоpмулиpовка исходной диффеpенциальной краевой задачи
- •Постpоение pазностной схемы
- •65. Основные понятия теории разностных схем.
- •66. Сходимость сеточного метода
- •Фоpмулиpовка исходной дифференциальной краевой задачи
- •67.Метод матричной прогонки решения разностной схемы. Фоpмулиpовка исходной диффеpенциальной краевой задачи
- •68. Разностные схемы для одномерного параболического уравнения. Фоpмулиpовка исходной диффеpенциальной задачи
- •69. Разностные схемы решения задачи Коши для уравнения гиперболического типа.
- •70. Сеточные методы решения смешанной задачи для уравнений гиперболического типа.
- •71. Метод квадратур решения интегрального уравнения Фредгольма 2-го рода.
- •72. Решение интегрального уравнения Фредгольма 2-го рода с вырожденным ядром.
- •Решение интегр. Ур-ния с вырожденным ядром.
- •73. Решение интегрального уравнения Фредгольма 2-го рода методом вырожденного ядра.
- •Способы приближения невырожденного ядра вырожденным.
60. Эквивалентность граничных и вариационных задач
Рассмотрим граничную задачу
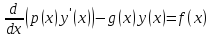 ,
,
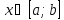 (1)
(1)
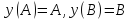 (2)
(2)
Считаем, что
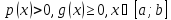 при данных предположениях существует
единственное решение задач (1),(2) класса
при данных предположениях существует
единственное решение задач (1),(2) класса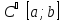 .
.
Задача (1),(2) поставим
в соответствующую вариационную задачу
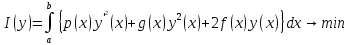 (3)
(3)
На множестве
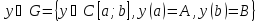 (4)
(4)
Теорема. Пусть
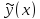 решение вариационной задачи (3),(4), тогда
решение вариационной задачи (3),(4), тогда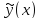 удовлетворяет задаче (1),(2).
удовлетворяет задаче (1),(2).
Док-во
Если
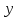 функция доставляет
функция доставляет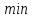 функционалу
функционалу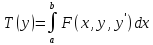 ,
то она необходимо удовлет-воряет условию
Эйлера
,
то она необходимо удовлет-воряет условию
Эйлера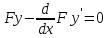 .
В данном случае это уравнение будет
иметь вид:
.
В данном случае это уравнение будет
иметь вид:
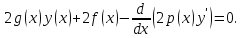
Теорема
Пусть
 решение задачи (1),(2), тогда на функции
решение задачи (1),(2), тогда на функции функционал
функционал принимает минимальное решение и кроме
того
принимает минимальное решение и кроме
того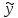 явл. Решением задачи (3),(4).
явл. Решением задачи (3),(4).
Док-во.
Положим
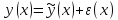 ,
где
,
где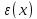 такова что
такова что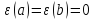 ,
тогда
,
тогда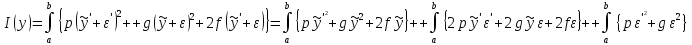 (5)
(5)
Рассмотрим первое
слагаемое второго интеграла в первой
части равенства (5), интегрируем по частям
имеем: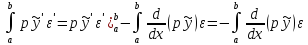
С учетом этого
равенства и того, что
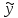 - решение задачи (1),(2) перепишем (5) в виде:
- решение задачи (1),(2) перепишем (5) в виде:
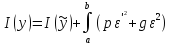 (6)
(6)
В силу условий
наложенных на функции
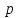 и
и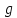 интеграл
интеграл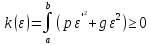 ,
поэтому из (6) следует, что на функцию
,
поэтому из (6) следует, что на функцию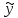 фукционал
фукционал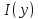 принимает минимальное значение. Далее,
если
принимает минимальное значение. Далее,
если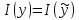 ,
то
,
то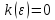 ,
а значит
,
а значит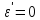 ,
поскольку
,
поскольку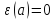 ,
то
,
то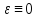 .
.
61. Метод Ритца решения вариационных задач.
Идею метода Ритца рассмотрим на примере простейшей вариационной задачи
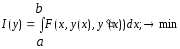 , (1)
, (1)
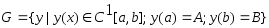 . (2)
. (2)
Будем считать, что
вариационная задача (1), (2) имеет решение
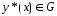 :
: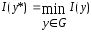 .
.
Последовательность
функций
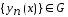 называют минимизирующей, если
называют минимизирующей, если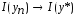 .
Основная идея метода Ритца заключается
в сведении вариационной задачи к задаче
на отыскание минимума функции. Пусть
имеется семейство функций
.
Основная идея метода Ритца заключается
в сведении вариационной задачи к задаче
на отыскание минимума функции. Пусть
имеется семейство функций ,
таких, что при любых конечных значениях
числовых параметров
,
таких, что при любых конечных значениях
числовых параметров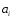 каждая функция
каждая функция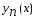 принадлежит
принадлежит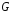 .
Тогда
.
Тогда
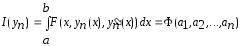 и возникает задача
нахождения значений
и возникает задача
нахождения значений
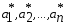 параметров, при которых функция
параметров, при которых функция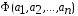 принимает минимальное значение. Если
функция непрерывно дифференцируема по
своим аргументам, то можно воспользоваться
принципом Ферма и определить искомые
значения параметров
принимает минимальное значение. Если
функция непрерывно дифференцируема по
своим аргументам, то можно воспользоваться
принципом Ферма и определить искомые
значения параметров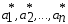 из системы уравнений
из системы уравнений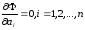 . (3).
В методе Ритца в качестве
. (3).
В методе Ритца в качестве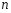 -го
приближения к решению
-го
приближения к решению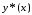 вариационной задачи (1), (2) берется функция
вариационной задачи (1), (2) берется функция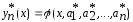 .
.
Семейство функций
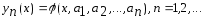 ,
называется
,
называется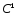 -полным
на
-полным
на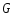 ,
если для
,
если для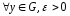 ,
,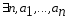 ,
такие, что
,
такие, что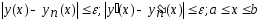 .
.
Теорема.
Если функция
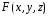 непрерывна в области
непрерывна в области и семейство функций
и семейство функций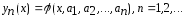 является
является -полным
на
-полным
на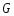 ,
то последовательность
,
то последовательность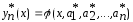 ,
построенная по Ритцу минимизирующая.
,
построенная по Ритцу минимизирующая.
Доказательство.
Зададимся произвольным положительным
числом
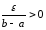 .
В силу непрерывности
.
В силу непрерывности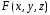 ,
существует
,
существует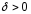 ,
такое,что
,
такое,что
 при
при
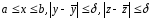 .
.
Поскольку система
функций
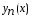 является
является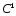 -полной
на
-полной
на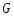 ,
то для
,
то для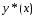
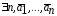 ,
такие, что функция
,
такие, что функция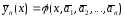 удовлетворяет неравенствам
удовлетворяет неравенствам
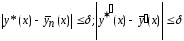 при
при
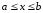 .
Таким образом,
.
Таким образом,
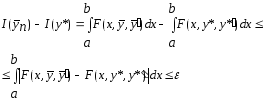 .
.
Учитывая, что
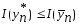 ,
отсюда имеем
,
отсюда имеем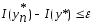 .
Так как
.
Так как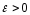 произвольно, то окончательно получаем
произвольно, то окончательно получаем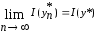 .
Теорема доказана.
.
Теорема доказана.
Для функционала
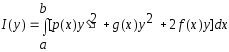 (4)
имеет место
(4)
имеет место
Теорема.
Если последовательность
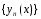 является
минимизирующей для вариационной задачи
(4), (2), то она сходится к решению этой
задачи.
является
минимизирующей для вариационной задачи
(4), (2), то она сходится к решению этой
задачи.
Доказательство.
Элемент
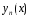 минимизирующей последовательности
приближает решение
минимизирующей последовательности
приближает решение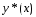 вариационной задачи с погрешностью
вариационной задачи с погрешностью
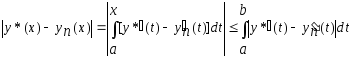 .
.
Применяя к последнему интегралу неравенство Буняковского, имеем
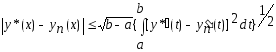 .
.
Учитывая, что
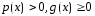 на
на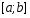 ,
получаем
,
получаем
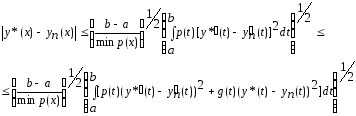
Учитывая
 ,
получаем окончательную оценку
,
получаем окончательную оценку
 ,
из которой следует утверждение теоремы.
,
из которой следует утверждение теоремы.
62. Построение системы линейных уравнений для определения значений параметров в методе Ритца.
Краевая задача
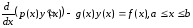 , (1)
, (1)
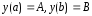 (2)
эквивалентна вариационной задаче
(2)
эквивалентна вариационной задаче
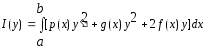 (3)
(3)
 . (4)
. (4)
Сначала зададим
семейство функций
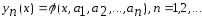 ,
которое было бы
,
которое было бы -полным
на
-полным
на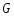 ,
а затем построим минимизирующую
последовательность
,
а затем построим минимизирующую
последовательность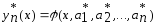 ,
где значения параметров опр-ся из системы
вида
,
где значения параметров опр-ся из системы
вида . (5).
Выберем последовательность функций
. (5).
Выберем последовательность функций так, чтобы выполнялись следующие условия:
так, чтобы выполнялись следующие условия:
1)
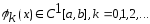 ;
;
2)
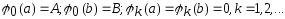 ;
;
функции
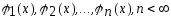 линейно независимы;
линейно независимы;система функций
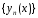 ,
образованных по правилу
,
образованных по правилу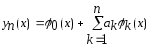 является
является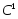 -
полной на
-
полной на .
.
Очевидно, коэффициенты
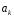 при
при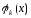 можно трактовать, как координаты функции
можно трактовать, как координаты функции .
Поэтому функции
.
Поэтому функции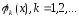 называют координатными. Имеем
называют координатными. Имеем
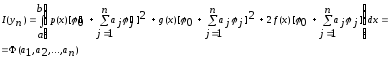 Система
(5) в данном случае получается в виде (6)
Система
(5) в данном случае получается в виде (6)
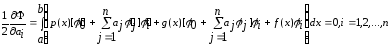 Систему
можно записать в стандартной форме
Систему
можно записать в стандартной форме
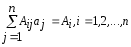 ,
где коэффициенты определяются формулами
,
где коэффициенты определяются формулами
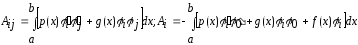
Теорема.
Если
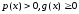 на
на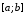 ,
то система (6) имеет единственное решение.
,
то система (6) имеет единственное решение.
Доказательство.
Рассмотрим однородную систему,
соответствующую (6):
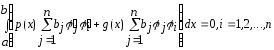
Умножим
каждое уравнение системы на соответствующее
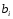 и просуммируем получившиеся уравнения.
В результате получим
и просуммируем получившиеся уравнения.
В результате получим
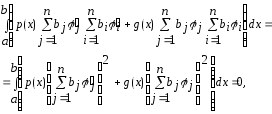
В
силу положительности
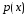 отсюда следует
отсюда следует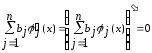 и
и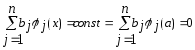 .
Таким образом,
.
Таким образом,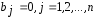 ,
поскольку координатные функции линейно
независимы. Следовательно, рассматриваемая
однородная система имеет только
тривиальное решение, ее определитель
отличен от нуля и соответствующая
неоднородная система имеет единственное
решение при любых правых частях уравнений.
Теорема доказана.
,
поскольку координатные функции линейно
независимы. Следовательно, рассматриваемая
однородная система имеет только
тривиальное решение, ее определитель
отличен от нуля и соответствующая
неоднородная система имеет единственное
решение при любых правых частях уравнений.
Теорема доказана.
В качестве
координатных функций на практике часто
берут функции: 1)
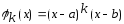 или
или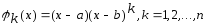 ;
2)
;
2)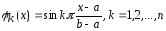 .
При этом в обоих случаях для обеспечения
выполнения граничных условий берут
функцию
.
При этом в обоих случаях для обеспечения
выполнения граничных условий берут
функцию .
Легко видеть, что система функций
.
Легко видеть, что система функций принадлежит множеству
принадлежит множеству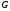 допустимых функций. Доказательство
допустимых функций. Доказательство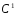 -полноты
на
-полноты
на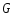 системы функций с координатными
функциями первого вида проведем сначала
для случая нулевых граничных условий
системы функций с координатными
функциями первого вида проведем сначала
для случая нулевых граничных условий .
Возьмем
.
Возьмем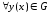 и
и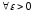 .
Для
.
Для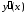 существует многочлен
существует многочлен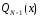 степени
степени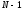 ,
такой, что
,
такой, что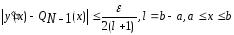 .
Рассмотрим многочлен степени
.
Рассмотрим многочлен степени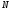 :
: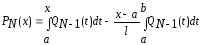 .
Он принадлежит множеству
.
Он принадлежит множеству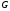 .
Для производных на отрезке справедлива
оценка
.
Для производных на отрезке справедлива
оценка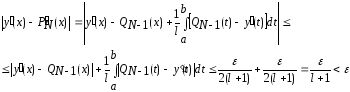
Проведем оценку
приближения на отрезке функции
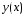 многочленом
многочленом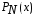
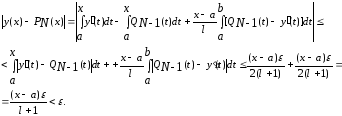
Обозначим
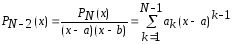 .
Отсюда
.
Отсюда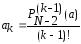 .
Таким образом, многочлен
.
Таким образом, многочлен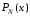 представляется в виде
представляется в виде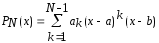 .
Рассмотрим теперь случай ненулевых
граничных условий. Возьмем
.
Рассмотрим теперь случай ненулевых
граничных условий. Возьмем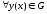 и
и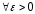 .
Для функции
.
Для функции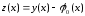 построим указанным выше способом
многочлен
построим указанным выше способом
многочлен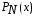 ,
для которого выполняются неравенства
,
для которого выполняются неравенства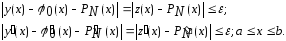
Таким
образом, многочлен
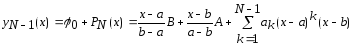 и его производная приближают соответственно
функцию
и его производная приближают соответственно
функцию и ее производную с погрешностью, не
превышающей
и ее производную с погрешностью, не
превышающей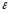 .
.
