13 . Оптимизация шага при численном диф-нии

Пусть функция 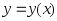задана на отрезке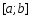таблицей значений.

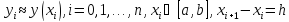Получим простейшую формулу численного дифференцирования. Используем разложение в ряд Тейлора

(1)

Из (1) имеем 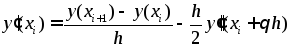(2)

Из (2) получили простейшую формулу численного дифференцирования: 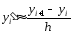. (3)

Подставим в формулу (3) точное значение производной и точные значения функции

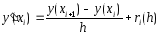
Величина 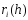представляет собой погрешность метода для численного дифференцирования по расчетной формуле(3).

Имеем 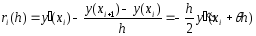.(4)

Из (4) для погрешности метода получаем оценку

. (5)

Из оценки (5) видно, что погрешность метода стремится к нулю при 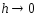. Учтем еще, что заданные величины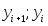приближают соответствующие значения функции с абсолютной погрешностью: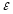

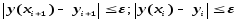.(6)

Тогда приходим к равенству 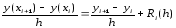, где величину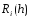называют неустранимой погрешностью.

Оценим неустранимую погрешность. Из последнего равенства имеем

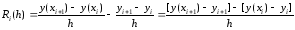
Отсюда с учетом (6) получим оценку 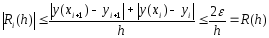.(7)

Из оценки (7) видно, что неустранимая погрешность стремится к бесконечности при .

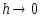Пренебрегая вычислительной погрешностью, для общей погрешности получаем оценку

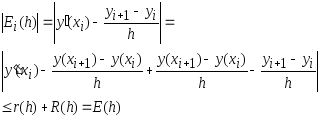
Найдем теперь оптимальную величину шага, при которой общая оценка погрешности (8)

будет минимальной. Из уравнения

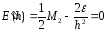
находим искомую величину шага .

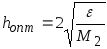При этом для общей погрешности получается минимальная оценка .

14. Интерполяционные квадратурные формулы

Будем рассматривать задачу приближенного вычисления значения определенного интеграла вида 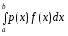.(1)

Здесь 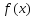- произвольная достаточно гладкая функция, а- некоторая фиксированная функция, называемая весовой функцией.

Для численного вычисления интеграла I(f) исп.квадратурные формулы:

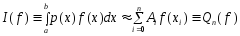. (2)

Точки 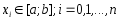называютузлами квадратурной формулы, 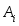- коэффициентами квадратурной формулы,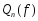- квадратурной суммой.

Заменяя функцию 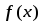в интеграле (1) интерполяционным многочленом Лагранжа по узлам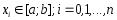, получим

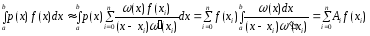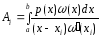, где . (3)

Квадратурные формулы (2), в которых коэффициенты определяются выражениями (3), называют интерпол-ми. Как видно из выражения (3), коэффициенты квадратурной формулы зависят от весовой функции 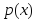, узлов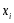и не зависят от функции.

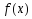Теорема. Для того чтобы квадратурное правило (2) было точным для любого многочлена 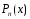степениn, необходимо и достаточно, чтобы оно было интерполяционным.

Д-во. Необх. Квадратурное правило (2) является точным для любого многочлена степени n. Возьмем произвольное значение 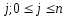и зафиксируем его. Для многочлена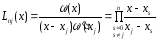степениn по формуле (2) имеем 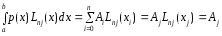. Т.о, все коэффициенты квадратурного правила (2) определяются формулой (3), то есть, квадратурное правило является интерполяционным.

Достат. Квадратурное правило (2) является интерполяционным. Возьмем произвольный многочлен 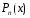степениn. Он, очевидно, совпадает со своим интерполяционным многочленом 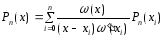. Поэтому

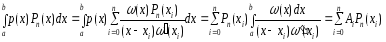Т.о., интерполяционное квадратурное правило является точным для любого многочлена степени n. Теорема доказана.

15. Квадратурные формулы Ньютона-Котеса

Рассмотрим построение интерпол-ных квадратурных ф-ул 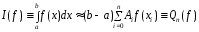(1)для следующих двух случаев расположения на отрезке интегрирования равномерной сетки узлов квадратуры:

1) ;

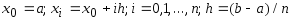2)

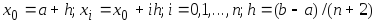
Если ввести параметр k, то оба случая можно записать в форме (2)

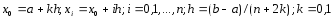Пределы интегрирования тогда представляются выражениями 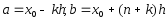. Перейдем также к новой переменной интегрированияy по правилу 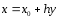. В результате получим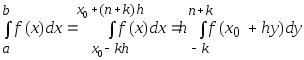.(3)

Для узлов квадратуры при этом имеем 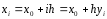. Т.о., новой переменной интегрирования соотв-ют узлы квадратуры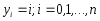. Подынтегральную ф-цию в правой части (3) заменим интерпол-ным мн-ном по узлам: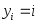

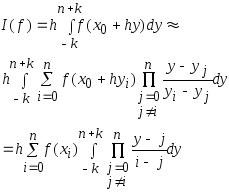
_{Поскольку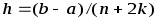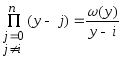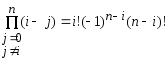};;, приходим к выражению.

Построена квадратурная формула вида (1), где коэффициенты определяются выражением

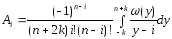. (4)

Квадратурные формулы (1) с равноотстоящими узлами (2) и коэфф-нтами (4) называют квадратурными формулами Н-Кот.