32. Разложение симметричных матриц. Метод квадр. Корней решения лин. Алг.Систем

Пусть A=[a_ij]_n×n данная симметричная матрица a_ij=a_ji. Будем строить разложение матрицы А в виде А=U^TU (1), где U- верхняя (правая) треугольная матрица. Равенство (1) перепишем в подробной форме:

(2)

Перемножив (2) и учитывая симметричность матрицы А, получаем систему уравнений относительно неизвестных u_ij:

u₁₁²= a₁₁ u₁₂u₁₁=a_{12 ………} u_1nu₁₁=a_1n

u₁₂²+ u₂₂²=a_{22 ……..} u_1nu₁₂+u_2nu₂₂=a_2n (3)

. . . . . . . . . . . . . . . . . . . . . . .

u_1n²+u_2n²+…+u_nn²=a_nn

Cистему (3) решаем следующим образом, в начале находим элемент u₁₁= 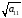, далее из остальной части 1-ой строки находим.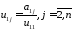

Из 1-го ур. во 2-ой строке находи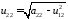м . Из остальной части 2-ой строки находим: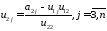

Продолжая, последним находим элемент:

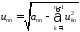
, указанный процесс можно описать следующими формулами: 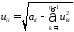(4)

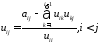(5)

При практическом счёте необходимо своевременно переключаться с формулы (4) на (5), и наоборот.

Замечание. Более универсально, чем разложение (1) явл. разложение эрмитовых матриц: А=U^*ΔU, где Δ-диагональная матрица на главной диагонали, которой стоят числа ±1.

Замечание: Реализацию вычисления по формуле (4), (5) могут помешать 2 обстоятельства:

- отрицательное подкоренное выражение в (4);

- обращение в 0 знаменателя (5).

Однако, если матрица А симметрична, положительно определённая, то разложение (1) всегда осуществляеться тоже самое отномительно к матрицам с диагоналями преобладанием.

Применим разложение (1) к решению лин. алг. системы Ах=b (6) с симметрично положительно определённой матрицей А. В силу (1) имеем:

U^TUx=b (7)

Перепишем (7) в виде 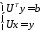(8)

Очевидно, что решение подсистемы (8) не сложнее, чем обратный ход метода Гаусса.

33. Метод вращения решений лин. алг. систем

Предположим, что решение системы лин. алг. ур.

Ах= b, с матрицей

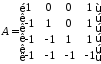
Прямой ход метода Гаусса даст следующую цепочку

Очевидно, что матрица такого типа размера n×n. После прямого хода метода Гаусса, допускает рост элементов до величены 2^n-1, что при больших n приводит к сильному влияниюпогрешности округлений.

Рассмотрим метод вращений решения лин. алг. систем не допуская большого роста абсолютных велечин элементов матрицы системы. Пусть задана система:

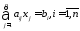(1)

Возьмём 2 числа С₁ и S₁ умножим 1-ое ур. системы на С₁ , 2-ое на S₁. Полученные уравнения сложим и заменим этим уравнением 1-ое ур. системы, т.е. 1-ое ур. сист. будет иметь вид:

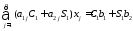
Далее 1-ое ур. сист. умножим на (-S₁), а 2-ое умножим на С₁, сложив, получим уравнения и заменим 2-ое ур. в 1, т.е. 2-ое ур. в 1 будет иметь вид:

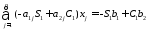
Перейдём к выбору чисел С₁ и S₁, выберем их таким образом, чтобы коэффициенты при х₁ во 2-ом ур. получилась система =0, т.е. чтобы выполнялось условие:

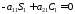
также потребуем, чтобы имело место условие нормировки: 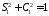. Тогда можно положить

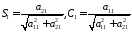
После указанного преобразования система (1) имеет вид:

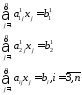(2)

Заметим, что числа С₁ и S₁ можно трактовать, как sin и cos некоторого угла, поэтому очевидно, что переход от (1) к (2) представляет собой преобразование вращения с некоторой ортогональной матрицей.

Предположим преобразуем исходную систему, 1-ое и 3-ее ур. в (2) и проведя те же рассуждения. Исключим из 3-го ур. в (2) перемножая x₁, далее берём 1-ое и 4-ое ур. получаем систему, 1-ое и 5-ое, и т.д. 1-ое и n-ое. Таким образом после указанных шагов система (2) преобразуется к виду:

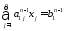(3)

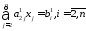(4)

Далее обрабатывая подсистему (4). Проведя аналогичные рассуждения для подсистемы (4) исключим неизвестную х₂ из всех уравнений подсистемы (4) начинаю со 2-го и т.д. продолжаем указанный процесс до тех пор, пока система (3), (4) не будет иметь треугольную матрицу, т.е. не будет приведена к виду:

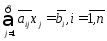(5)

Теперь нахождение неизвестных из системы (5) аналогично обратному ходу метода Гаусса.

Преимущество этого метода заключается в том, что при переходе от системы (1) к системе (5) евклидова норма каждого столбца матрицы неизменяется. Действительно после 1-го шага имеем: