1.Метрические пр-ва. Шары, открытые и закрытые мн-ва.

Опр. Пусть - произвольное множество и пусть любым двум элементам сопоставлено неотрицательное число , обладающее следующими свойствами, называющимися аксиомами метрики:

1. (аксиома отделимости);

2. , (аксиома симметрии);

3. , (аксиома треугольника).

Аксиомы 1-3 называются аксиомами метрического пространства, называется метрикой на множестве , а множество, на котором задана метрика, называется метрическим пространством.

Опр. Открытым шаром с центром в т. радиуса r>0, где Х—МП, наз-ся мн-во .

Замкнутым шаром с центром в т. радиуса r>0, где Х—МП, наз-ся мн-во .

Сферой в т. радиуса r>0 наз-ся мн-во .

Пусть М--некоторое подмн-во Х и пусть есть т. . Т. наз-ся внутренней точкой мн-ва М, если сущ-ет некоторый открытый шар с центром в этой точке .

Совокупность всех внутренних точек мн-ва М наз-ся внутренностью мн-ва М и обозначается .

Мн-во М в метрическом пр-ве Х наз-ся открытым, если любая точка этого мн-ва явл-ся внутренней точкой; это означает, что . Пример: открытый шар.

Св-ва открытых мн-в: 1.  и пр-во Х явл-ся открытым.

2.Если есть любое семейство открытых мн-в ( ) , -открытое для , то -открытое.

3.Если , -открытые, то -открыты.

Совокупность всех открытых мн-в обозначают и наз-ют топологией пр-ва Х.

Св-ва:

1’., X.

2’. ( ), ;

3’. .

Х-топологическое пр-во.

Замкнутым мн-вом наз-ют мн-во, дополнение к-го открыто ( , если - открыто, то М- замкнуто).

Пусть MX—МП , т. наз-ся точкой прикосновения мн-ва М, если .

Замыканием мн-ва М наз-ся мн-во М, состоящее из всех точек прикосновения мн-ва М MM мн-во М замкнуто, если М=М.

Если .

Точка прикосновения, к-рая не принадлежит мн-ву М, наз-ся предельной точкой мн-ва М, т.е. MX—МП, , если содержит точку, к-рая не принадлежит М, т.е. .

Совокупность всех предельных точек мн-ва М наз-ся произвольным мн-вом к мн-ву М и обозначается M’.

Границей мн-ва М наз-ся мн-во . Пример, М=Q.

У мн-ва рациональных чисел нет внутренности , Q=R. Q=R.

Внешностью мн-ва М наз-ся внутренность его дополнения , .

2.Сходящиеся и фундаментальные последовательности в МП и их св-ва.

Последовательностью наз-ся отобр-ние мн-ва натурал. чисел в Х, т.е. NX, х(n)= -общий n-ый член посл-ти.

( )-упорядоченное мн-во значений посл-ти.

Определение. Последовательность ( ) сходится к эл-ту aX, если расстояние ,т.е. .

Элемент а называется пределом последовательности .

Св-во:Если последовательность сходится, то предел этой последовательности единственен.

Доказательство.

Будем доказывать методом от противного. Пусть , ab. Т.к. .

Т.к. , то .

Обозначим . Тогда (1) и (2).

Возьмем . Тогда в силу (1) (a,b)2. При 0 (a,b)0. С др. стороны по аксиоме 1: (a,b)0 (a,b)=0a=b. Это противоречит предположению, а  предел единственен.

Определение. Последовательность в метрическом пространстве называется фундаментальной, если .

Св-во:если последовательность сходится, то она фундаментальна, т.е. любая сходящаяся посл-ность фундаментальна.

Доказательство.

Зафиксируем произвольное . Возьмём . Так как сходится, то и .

.

Т. обр мы доказали, что -фундаментальна.

Определение. Метрическое пространство , в котором любая фундаментальная последовательность сходится, называется полным метрическим пространством. Обратное верно всегда.

Определение. Подмножество , - метрическое пространство, называется подпространством этого метрического пространства, если в введена метрика из метрического пространства , то есть , где - метрика и пара - подпространство метрического пространства с - индуцированной метрикой пространства .

3.Пр-во и его св-ва. Теорема о его полноте.

- пространство всех непрерывных функций на отрезке .Пусть f,gC[a;b] --Чебышевская метрика в пр-ве .

Докажем, что функция является метрикой:

1) , то есть

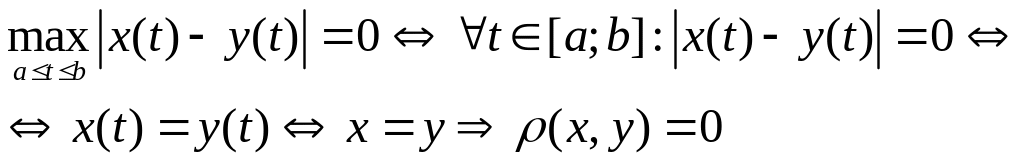
2)

3)

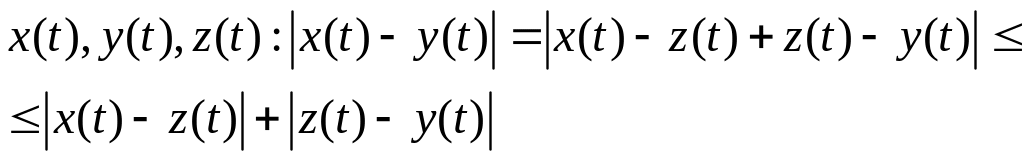
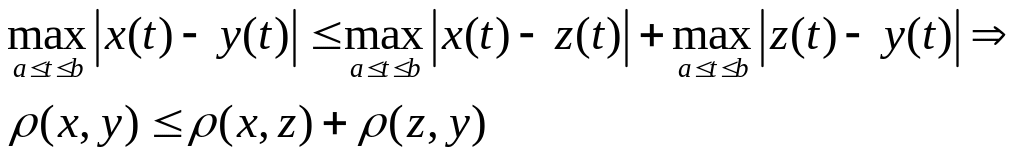
Теорема. Пр-во --полное.

Д-во: Возьмем произвольную фундаментальную посл-ность ( ) в пр-ве и докажем, что оно сходится.

Т.к. ( ) фундаментальна, то имеем: >0 (1).

Отметим, что если выполняется (1), то t[a;b]. (2).

Зафиксируем t[a;b] и рассмотрим числовую посл-ность ( ). Исходя из (2) числовая посл-ность ( ) фундаментальна в пр-ве R, к-рое явл. полным  сущ-ет такое а , что . Построим числовую ф-цию (3). Тогда в силу (3) .

Докажем, что равномерно и непрерывна в .

В пределе мы получим на [a;b].

Т.к. непрерывна на и , то f(t) непрерывна в . Т.к. fC[a;b], то в .

Получили, что пр-во полно.

Интегральная метрика в пр-ве . Эта метрика превращает пр-во в пр-во -неполное.

- пространство всех непрерывно дифференцируемых функций на .

.

4.Примеры метрич пр-в (2-4)

2) Множество и для рассмотрим метрику

делает пространством изолированных точек, что обозначается .

Выясним, явл-ся ли это пр-во полным. Для этого возьмем фундаментальную посл-ность и .

.Посл-ность, у к-рой с некоторого номера все значения равны 0 , наз-ся финально-стационарной .

Получили, что , что .

Т. обр доказали, что любая фундаментальная посл-ность явл-ся финально-стационарной. Любая финально-стационарная посл-ность сходится  пр-во полное.

3) Пусть – произвольное натуральное число, обозначим через функцию, определенную на отрезке .

Если , то , , если же , то - пространство всех - раз непрерывно дифференцируемых функций на , . Тогда

4) -пространство всех бесконечно дифференцируемых функций на .

Если , то

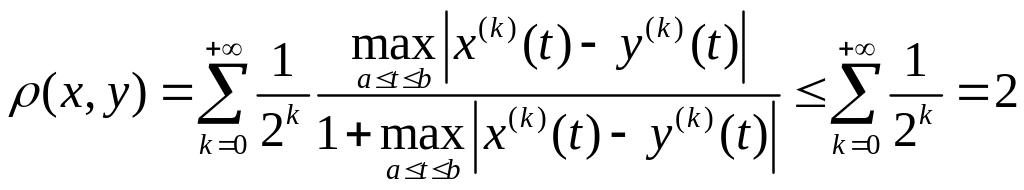
Покажем, что удовлетворяет всем аксиомам метрики:

1)

Проверим, что если , то , т.е. Если , то , т.е.

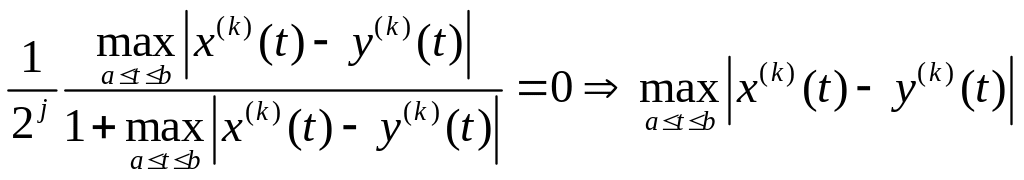
2) выполняется, по свойствам модуля.

3) , т.е.

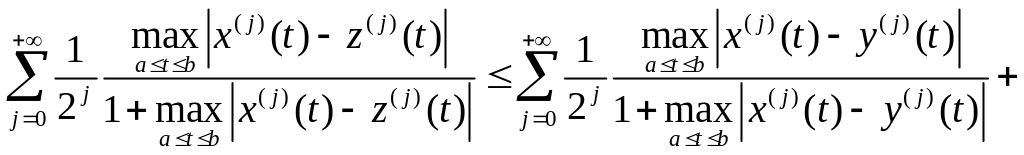
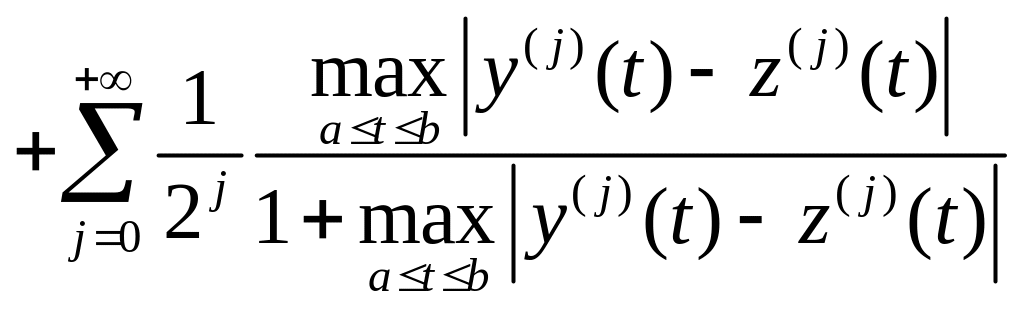(1)

Для доказательства используем свойства ряда. Достаточно доказать неравенство без сумм для Обозначим через a,b,c наши дроби.

(2)

Пусть , Докажем (2).

Введём вспомогательную функцию:

,

, значит функция возрастающая, следовательно,

.

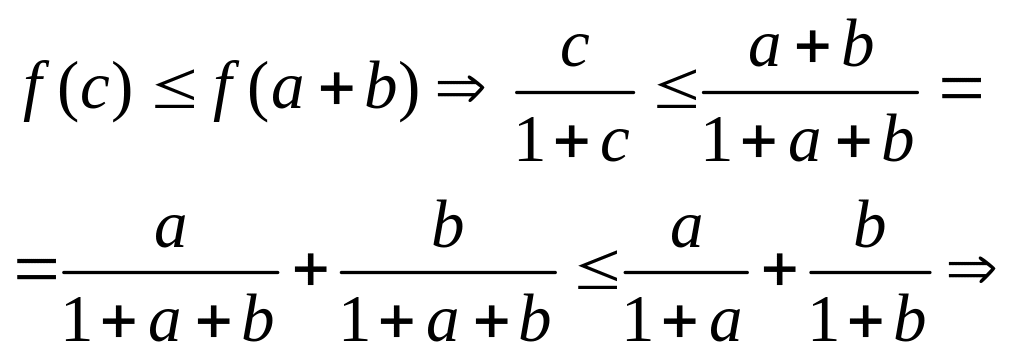
В знаменателях мы можем убрать , т.к. и от их удаления соответствующие дроби только возрастут.

Итак, доказали, что является метрикой.

5. Примеры метрич пр-в (5-7)

5)С(R)-пр-во всех непрерывных ф-ций на числовой прямой.

В этом случае берутся отрезки [-n;n]N. Тогда .

 С(R) удовлетворяет всем аксиомам метрического пр-ва.

6) --пр-во всех К-раз непрерывно диф-мых ф-ций на всей числовой оси.

.

7) -- пр-во всех бесконечно диф-мых ф-ций на всей числовой оси.

6. Примеры метрич пр-в (8-14)

8) S-пр-во всех числовых последовательностей с элементами - числовая последовательность. .

9) - пространство всех квадратично суммируемых последовательностей, ,

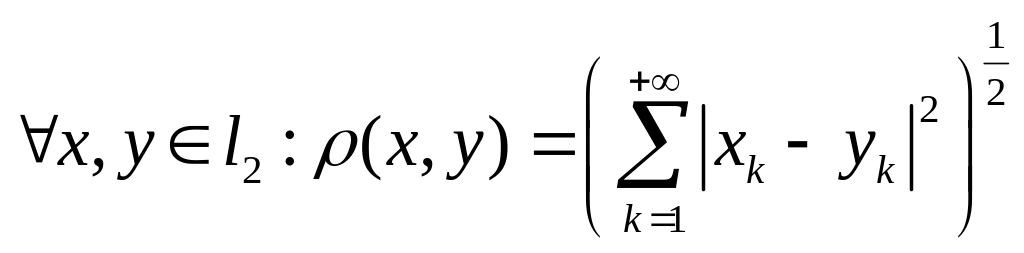
10) -пространство всех абсолютно суммируемых последовательностей. ,

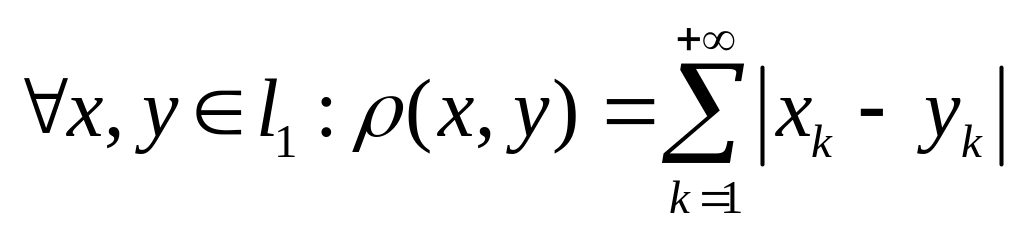
11) --пр-во всех числовых посл-тей, суммируемых в p-ой степени.

12) - пространство всех таких числовых последовательностей, которые являются ограниченными. Последовательность называется ограниченной, если существует число .

.

13) с – пространство всех сходящихся числовых последовательностей.

это сходящаяся последовательность, т.е.

,

- индуцированная метрика.

14) - пространство всех числовых последовательностей, сходящихся к нулю (бесконечно малые последовательности), его элементы , такие, что ,

. -замкнутое, полное

Вводится индуцированной метрикой из пространства .