
- •1.Метрические пр-ва. Шары, открытые и закрытые мн-ва.
- •7.Непрерывн. Отобр., св-ва.
- •8.Сжимающие отобр-я, св-ва
- •9. Принцип неподвижной точки
- •10.Полукольца мн-в и мера на полукольцах. Св-ва
- •11.Кольца мн-в и их св-ва
- •12.Теорема о распространении мера с полукольца на кольцо
- •13.Примеры мер, опр-ных на всех мн-вах
- •14.Внешняя мера и ее св-ва
- •15.Ступенчатые ф-ции
- •16.Интеграл от ступенчатой ф-ции
- •17.Интеграл от интегрируемой ступенчатой ф-ции
- •18.Измеримые ф-ции и их св-ва
- •19.Сходимость почти всюду. Канторово мн-во.
- •20.Интегрируемые ф-ции. Интеграл Лебега.
- •22.Тензорное произведение мер
- •23. Теорема о тензорном произведении мер.
- •24. Двойные и повторн инт от тенз произв. Т.Фубини и Тонелли.
- •26.Векторные подпр-ва и фактор пр-ва
- •28.Порождающие мн-ва. Базисы. Теорема о сущ алг базиса.
- •29.Линейный оператор. Св-ва.
- •30.Линейные функционалы. Теорема Хана-Банаха.
11.Кольца мн-в и их св-ва
Определение.
Пусть
![]() .
.
![]() называется
кольцом, если оно обладает сл св-вами:
называется
кольцом, если оно обладает сл св-вами:
1)
![]() 2)
2)![]()
Кольцо обладает следующими свойствами:
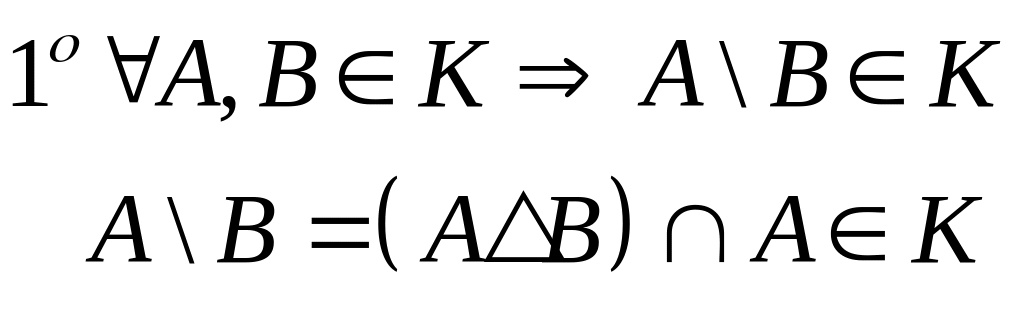 .
.
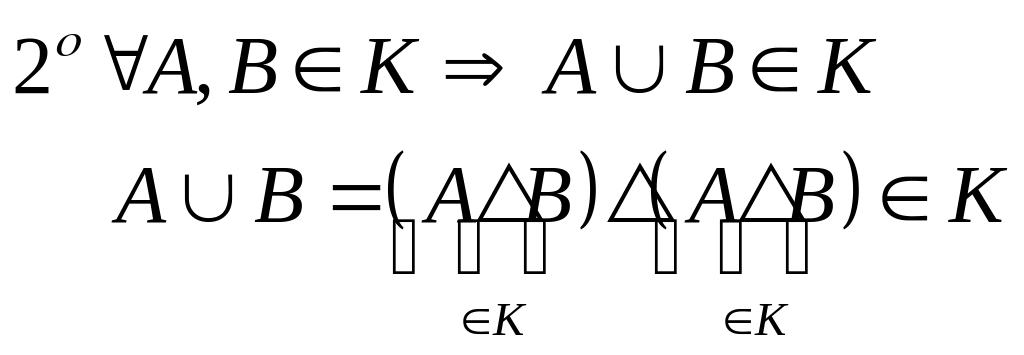
![]() т.к.
т.к.
![]()
![]()
Кольца, содержащие , называются алгеброй.
Замечание.Если К-кольцо, то К-полукольцо. В силу св-ва 1:
A\BK CK A\B=C
Определение. Пусть S—полукольцо. Через K(s) обозначим множество непересекающихся объединений:
![]()
Теорема (о кольце, порожденном полукольцом).
Если S – полукольцо то K(s) – кольцо.
Доказательство.
Пусть
![]() ,
,
![]() где
где
![]()
Рассмотрим
![]() и покажем, что
и покажем, что
![]()
I.
![]()
![]()
Покажем, что
![]()
Будем доказывать
методом математической индукции
(индукцию проводим по![]() ):
):
Если
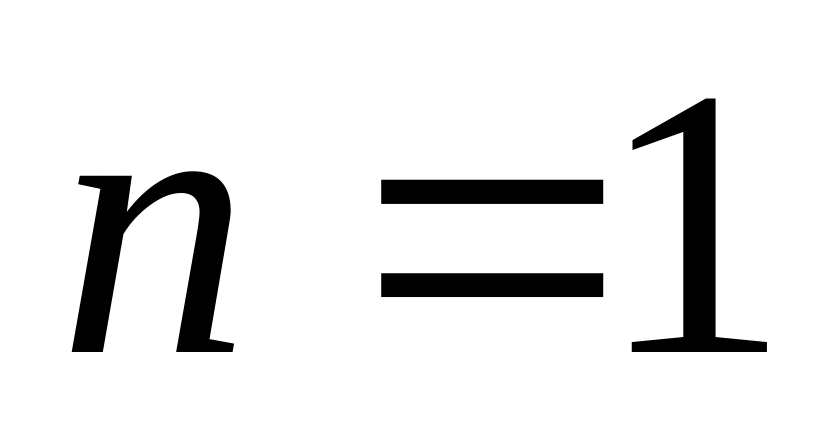 ,
то
,
то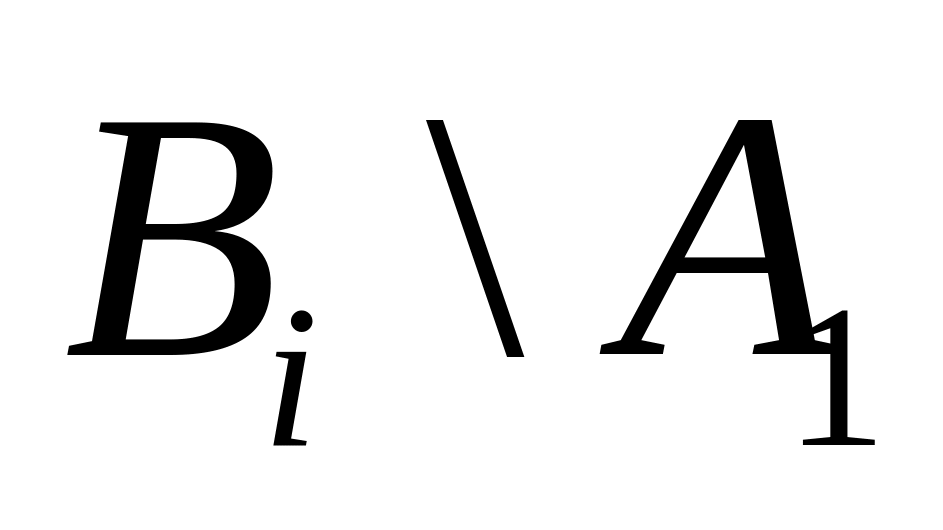 :
: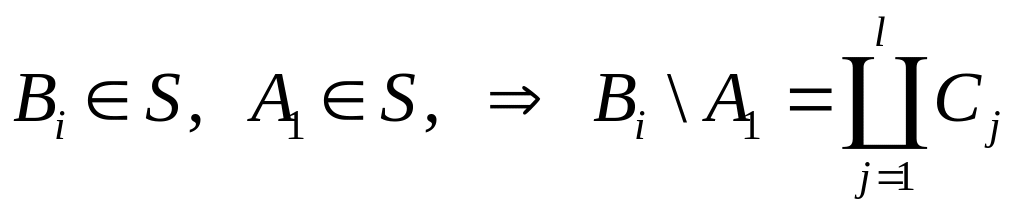 ,
где
,
где
![]()
Пусть наше утверждение
 верно
при
верно
при
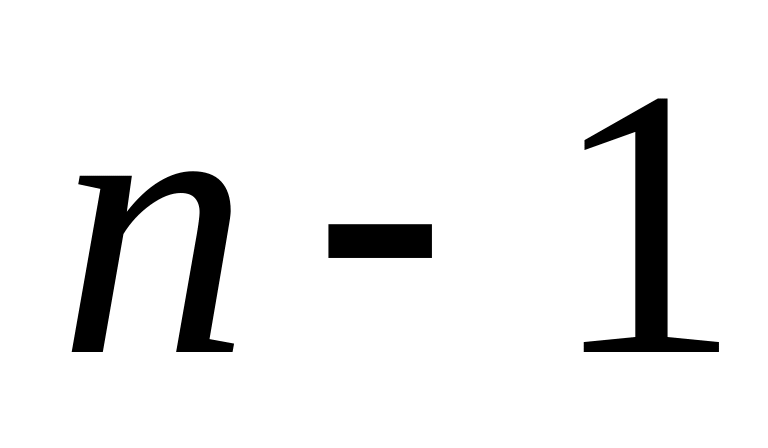 ,
т.е.
,
т.е.
 .
Покажем, что оно справедливо и для
:
.
Покажем, что оно справедливо и для
:
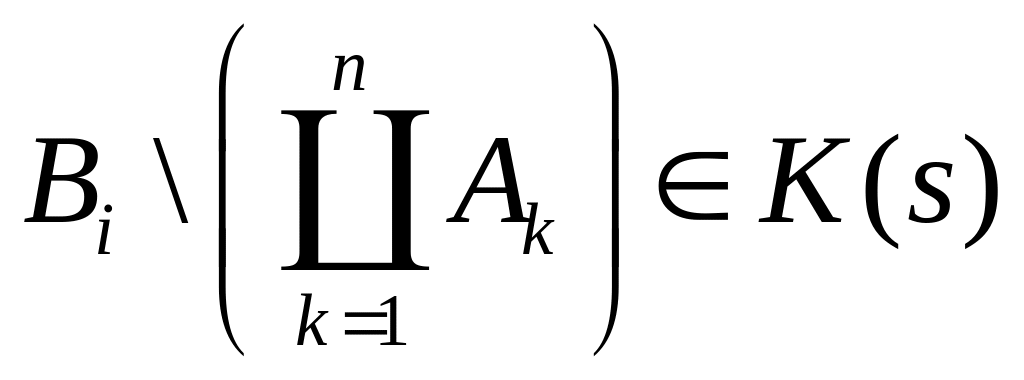 ,
,
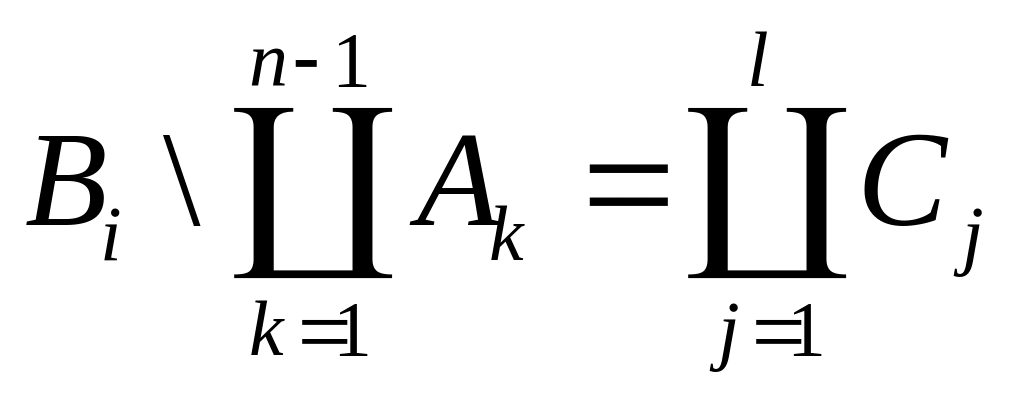 тогда можно записать:
тогда можно записать:
![]()
Таким образом,
доказали, что
![]() из
справедливо:
из
справедливо:
![]()
II. Рассмотрим
![]()
Т.о. показали, что
![]()
Тогда
![]()
![]()
![]()
Мы доказали, что
![]() и
и
![]() -- кольцо.
-- кольцо.
12.Теорема о распространении мера с полукольца на кольцо
Пусть мера
задана на полукольце
![]() , тогда мера
единственным образом распространяется
на порождаемое кольцо К(
),
а именно
, тогда мера
единственным образом распространяется
на порождаемое кольцо К(
),
а именно
![]()
![]() (1)
(1)
Д-во:
Для
![]() возьмем
возьмем
![]() ,
тогда
,
тогда
![]() ,
,
где
![]() - распространение (расширение) прежней
меры
- распространение (расширение) прежней
меры
![]()
Если
![]() ,
то по (1) получаем
,
то по (1) получаем
![]() (2)
(2)
Определение, которое дается формулой (1), корректно, т.к. правые части (1) и (2) равны. Проверим это.
Введем обозначение
![]() ,
,
![]() .
Части
.
Части
![]() не пересекаются.
не пересекаются.
Рассмотрим
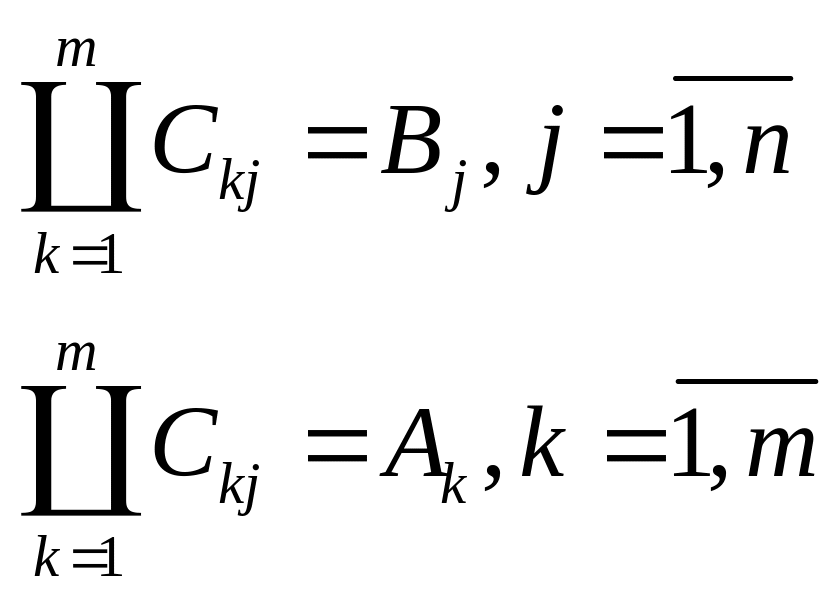
Рассмотрим правую часть (1), т.е.
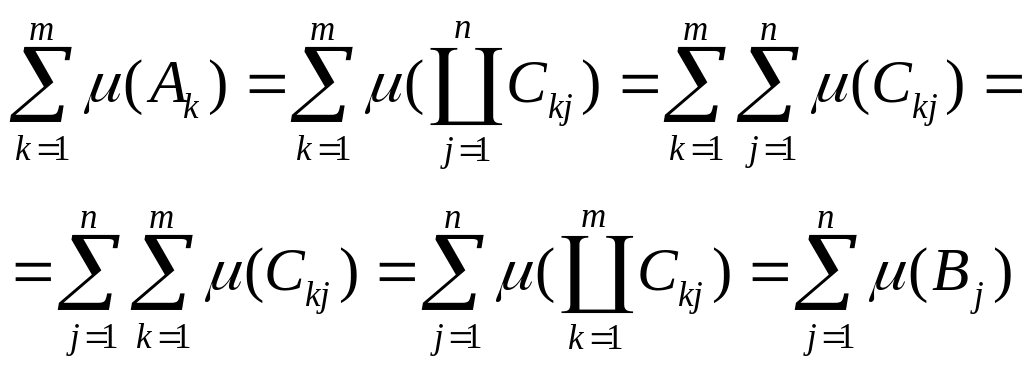
Таким образом, мы доказали, что правые части (1) и (2) равны.
Будем говорить,
что
![]() - мера на кольце K(S).
Докажем, что эта мера неотрицательна и
аддитивна.
- мера на кольце K(S).
Докажем, что эта мера неотрицательна и
аддитивна.
Доказательство.
То, что она неотрицательна
 из (1) как сумма неотрицательных чисел,
из (1) как сумма неотрицательных чисел,

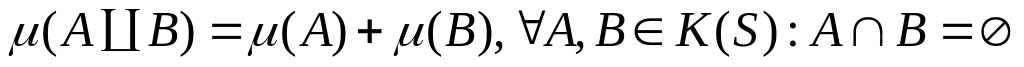
Докажем это.
![]()
![]()
![]()
Т.к. по условию
![]() ,
то их части тоже не пересекаются, т.е.
,
то их части тоже не пересекаются, т.е.
![]()

т.е.
![]() - мера на кольце
- мера на кольце
![]() (является расширением первоначальной
меры на
).
(является расширением первоначальной
меры на
).
13.Примеры мер, опр-ных на всех мн-вах
, где Х—произвольное мн-во.
Определение.
Мера
,
заданная на
![]() ,
называется
,
называется
![]() - аддитивной, если
- аддитивной, если
![]() ;
причем
;
причем
![]() ,
то
,
то
![]() .
.
,
возьмем точку
![]() и определим меру
и определим меру
![]() :
:
![]()
Тогда
называется атамарной мерой, сосредоточенной
в точке
![]() .
.
Покажем, что это мера. Проверим аксиомы.
Неотрицательность следует из определения, т.е.
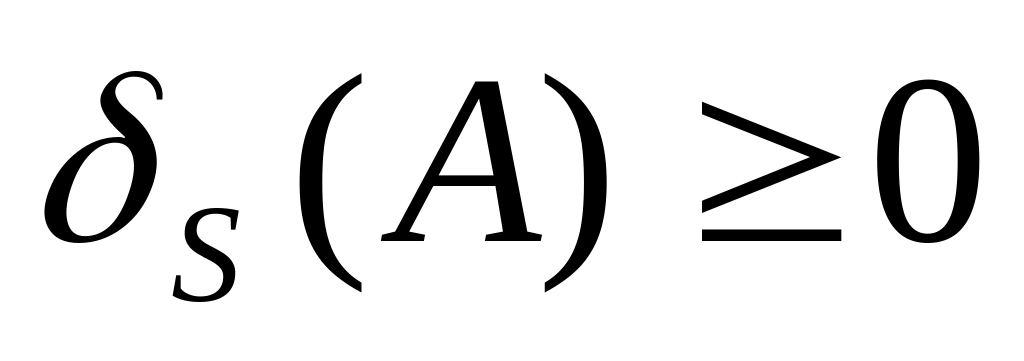
Проверим выполнение условия аддитивности.
![]()
Докажем, что
![]()
Пусть
 ,
тогда
,
тогда
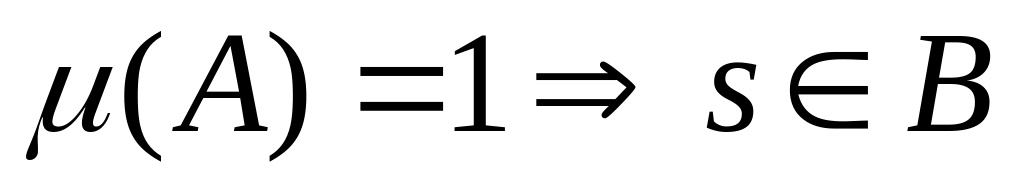 или
или
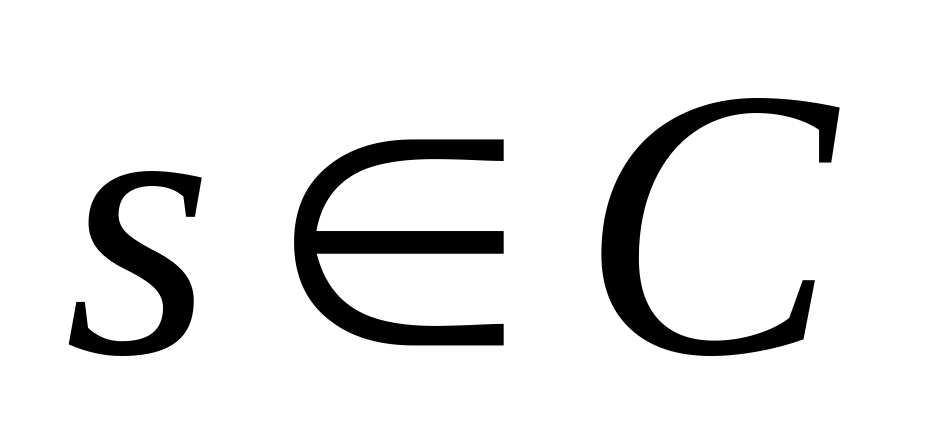 .
.
Пусть
![]() ,
тогда
,
тогда
![]() и
и
![]() .
В противном случае получаем
.
В противном случае получаем
![]() и
и
![]() или
или
![]() .
.
 ,
тогда
,
тогда
 ,
но
,
значит, т.к.
,
то
,
но
,
значит, т.к.
,
то
 и
,
то
и
,
то
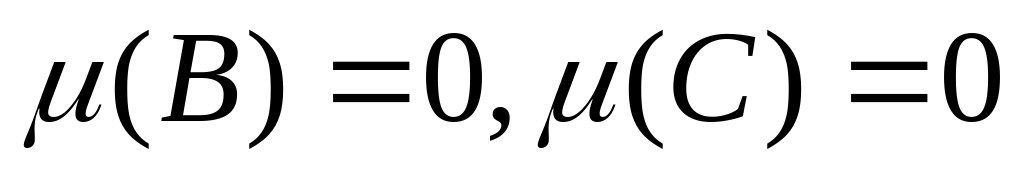 .
.
![]() является мерой.
является мерой.
Пусть
![]() .Докажем,
что
.Докажем,
что
![]() -аддитивная
мера.
-аддитивная
мера.
Для доказательства необходимо рассмотреть два случая:
1)
![]()
![]() верно равенство
верно равенство
![]()
2)
![]()
верно равенство
Доказали, что любая атамарная мера является -аддитивной мерой.
