
- •1.Метрические пр-ва. Шары, открытые и закрытые мн-ва.
- •7.Непрерывн. Отобр., св-ва.
- •8.Сжимающие отобр-я, св-ва
- •9. Принцип неподвижной точки
- •10.Полукольца мн-в и мера на полукольцах. Св-ва
- •11.Кольца мн-в и их св-ва
- •12.Теорема о распространении мера с полукольца на кольцо
- •13.Примеры мер, опр-ных на всех мн-вах
- •14.Внешняя мера и ее св-ва
- •15.Ступенчатые ф-ции
- •16.Интеграл от ступенчатой ф-ции
- •17.Интеграл от интегрируемой ступенчатой ф-ции
- •18.Измеримые ф-ции и их св-ва
- •19.Сходимость почти всюду. Канторово мн-во.
- •20.Интегрируемые ф-ции. Интеграл Лебега.
- •22.Тензорное произведение мер
- •23. Теорема о тензорном произведении мер.
- •24. Двойные и повторн инт от тенз произв. Т.Фубини и Тонелли.
- •26.Векторные подпр-ва и фактор пр-ва
- •28.Порождающие мн-ва. Базисы. Теорема о сущ алг базиса.
- •29.Линейный оператор. Св-ва.
- •30.Линейные функционалы. Теорема Хана-Банаха.
7.Непрерывн. Отобр., св-ва.
Рассмотрим два
метрические пространства
![]() с
метриками
с
метриками
![]() и
и
![]() соответственно.
соответственно.
Введем отображение
![]() .
.
![]()
![]() - образ
элемента
при отображении
- образ
элемента
при отображении
![]() .
.
Определение.
Отображение
называется непрерывным в точке
![]() ,
если
,
если
![]()
Шар
![]() для
для
![]() ,
шар
,
шар
![]() для
для
![]() .
.
Определение можно переписать следующим образом:
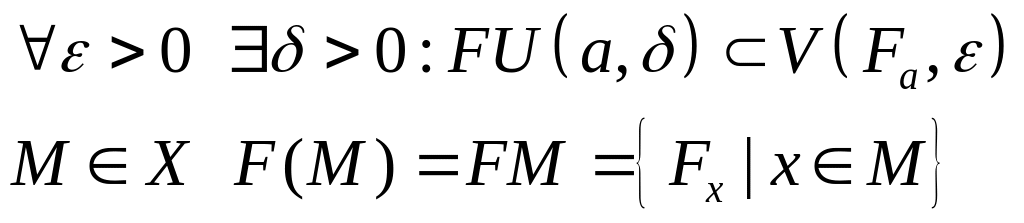
Теорема (об эквивалентном условии непрерывности).
Для того чтобы
отображение
было непрерывным в точке
необходимо
и достаточно, чтобы для любой
последовательности
![]() ,
сходящейся к
,
сходящейся к
![]() при
при
![]() :
:
![]() .
.
Если отображение
непрерывно в каждой точке
![]() ,
то говорят, что отображение
непрерывно на всем пространстве
и
называется непрерывным отображением.
,
то говорят, что отображение
непрерывно на всем пространстве
и
называется непрерывным отображением.
Множество всех
непрерывных отображений из
в
![]() обозначим
обозначим
![]() .
.
Теорема (о непрерывности композиции).
Пусть
![]() непрерывные отображения
,
непрерывные отображения
,
![]() ,
где
,
где![]() –
метрические пространства. Тогда
композиция отображений
–
метрические пространства. Тогда
композиция отображений
![]() (которая
определяется следующим образом
(которая
определяется следующим образом
![]() )
является непрерывным отображением
)
является непрерывным отображением
![]() .
.
(Кратко: композиция непрерывных отображений является непрерывным отображением).
Доказательство.
Возьмем произвольное
и
пусть последовательность
![]() ,
тогда, применяя теорему об эквивалентных
условиях непрерывности, получаем
,
тогда, применяя теорему об эквивалентных
условиях непрерывности, получаем
![]() .
Еще раз применяя эту теорему, получаем,
что
.
Еще раз применяя эту теорему, получаем,
что
![]() .
Это значит, что
.
Это значит, что
![]() (3)
(3)
И снова применяя предыдущую теорему, получаем, что непрерывно в , т.е. композиция непрерывна в точке . А т.к. точка была выбрана произвольно из множества , то отображение является непрерывным.
8.Сжимающие отобр-я, св-ва
Будем рассматривать отображение F:XY с метрикой .
Определение.
Отображение
F:XY ,
где X
и Y
метрические пр-ва, называется сжимающим
отображением
(отображением сжатия), если существует
число
![]() ,
что выполняется неравенство:
,
что выполняется неравенство:
![]() (*)
(*)
Св-во сжимающих отобр-ий.
Любое сжимающее отображение непрерывно.
Д-во.Для
этого выберем произвольную точку
.
Полагая
![]() ,
из соотношения (*) получаем:
,
из соотношения (*) получаем:
![]() (1).
(1).
![]() .
Тогда по заданному
можно построить
такое, что
.
Тогда по заданному
можно построить
такое, что
![]() (
(![]() .
Т.к.
.
Т.к.
![]() ,
то
,
то
![]() .
.
Таким образом,
![]() ).
А
это значит по определению, что отображение
непрерывно в точке
.
).
А
это значит по определению, что отображение
непрерывно в точке
.
Т.к. точка была выбрана произвольно из , то отображение непрерывно на всем пространстве.
Таким образом, любое сжимающее отображение непрерывно.
Определение.
Если имеем
отображение
![]() ,
то точка
называется
неподвижной
точкой отображения,
если
,
то точка
называется
неподвижной
точкой отображения,
если![]() .
.
Теорема (о единственности неподвижной точки у сжимающего отображения).
Пусть - сжимающее отображение, , тогда в отображении не может быть более одной неподвижной точки.
Доказательство.
Пусть существует
хотя бы две неподвижные точки у отображения
![]() .
.
Если![]() ,
,
тогда
![]()
Следовательно,
![]() (2)
(2)
Т.к.
![]() ,
то
,
то![]() .
.
Неравенство (2)
сокращаем на
и получаем,
![]() ,
что противоречит
.
,
что противоречит
.
