
- •1.Метрические пр-ва. Шары, открытые и закрытые мн-ва.
- •7.Непрерывн. Отобр., св-ва.
- •8.Сжимающие отобр-я, св-ва
- •9. Принцип неподвижной точки
- •10.Полукольца мн-в и мера на полукольцах. Св-ва
- •11.Кольца мн-в и их св-ва
- •12.Теорема о распространении мера с полукольца на кольцо
- •13.Примеры мер, опр-ных на всех мн-вах
- •14.Внешняя мера и ее св-ва
- •15.Ступенчатые ф-ции
- •16.Интеграл от ступенчатой ф-ции
- •17.Интеграл от интегрируемой ступенчатой ф-ции
- •18.Измеримые ф-ции и их св-ва
- •19.Сходимость почти всюду. Канторово мн-во.
- •20.Интегрируемые ф-ции. Интеграл Лебега.
- •22.Тензорное произведение мер
- •23. Теорема о тензорном произведении мер.
- •24. Двойные и повторн инт от тенз произв. Т.Фубини и Тонелли.
- •26.Векторные подпр-ва и фактор пр-ва
- •28.Порождающие мн-ва. Базисы. Теорема о сущ алг базиса.
- •29.Линейный оператор. Св-ва.
- •30.Линейные функционалы. Теорема Хана-Банаха.
23. Теорема о тензорном произведении мер.
Определение.
Пусть
![]() -
мера на полукольце
,
-
мера на полукольце
,
![]() -
мера на полукольце
и
-полукольцо.
Определим на полукольце S
- меру
-
мера на полукольце
и
-полукольцо.
Определим на полукольце S
- меру
![]() ,
где
,
где
![]()
![]() ,
,
![]() .
Тогда
-
называется тензорным
произведением
и
и записывается следующим образом:
.
Тогда
-
называется тензорным
произведением
и
и записывается следующим образом:
![]() .
.
Теорема (о тензорном произведении мер).
Тензорным
произведение мер является мерой, т.е.
если
-
мера на пространстве
,
а
-
мера на пространстве
,
то
![]() является мерой на пространстве
.
является мерой на пространстве
.
Доказательство.
I.
Возьмем
![]() -полукольца
множеств на пространствах
-полукольца
множеств на пространствах
![]() соответственно. Тогда
соответственно. Тогда
![]() представляется в виде:
представляется в виде:
![]() ,
где
,
где
![]() ,
тогда
,
тогда
![]() .
.
II.
Докажем, что если
![]() ,
где
,
где
![]() ,
тогда
,
тогда
![]() -
это свойство аддитивности меры
.
-
это свойство аддитивности меры
.
Для этого рассмотрим характеристическую функцию
![]() (1)
(1)
Т.к.
,
где
![]() ,
тогда
,
тогда
![]() (2)
(2)
Аналогично,
,
где
![]() ,
тогда
,
тогда
![]() (3)
(3)
Поскольку
,
то
![]() (4)
(4)
Подставляем (2), (3), (4) в (1):
![]() (5)
(5)
Т.к. характеристическая
функция множеств является интегрируемой,
то можно проинтегрировать равенство
по
![]() :
:
![]() Получаем:
Получаем:
![]() (6)
(6)
Полученное
соотношение (6) проинтегрируем по
множеству
![]() :
:
![]()
Получаем:
![]()
Из этого по определению следует: .
Таким образом, доказали аддитивность .
Итак, - неотрицательна и аддитивна, значит является мерой.
24. Двойные и повторн инт от тенз произв. Т.Фубини и Тонелли.
Интеграл от функции
![]() называется интегралом Лебега:
называется интегралом Лебега:
![]() ,
иногда пишут
,
иногда пишут
![]() .
.
Будем рассматривать интегралы
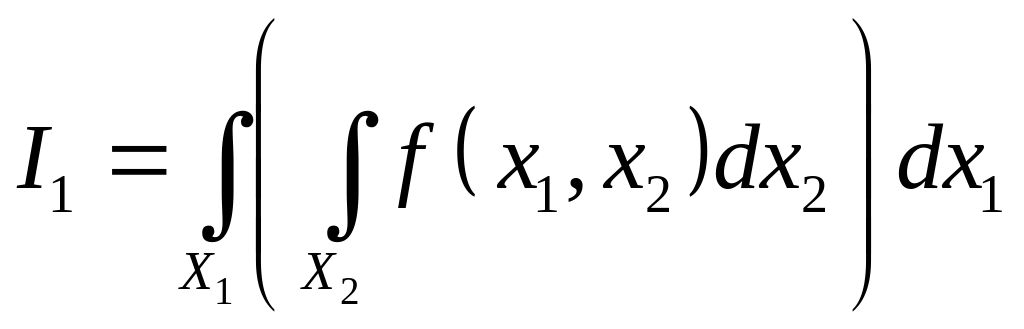 и
и
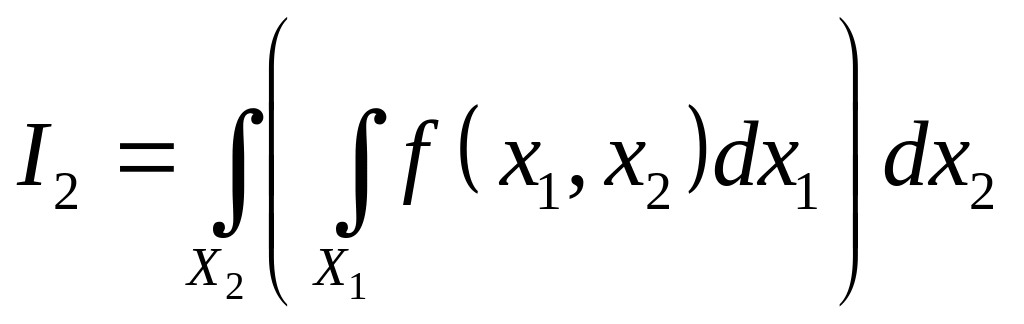 .
.
Эти интегралы называют повторными.
Теорема Фубини.(о связи между двойным интегралом и повторными интегралами)
Если функция
интегрируема по тензорному произведению
мер
![]() ,
т.е. существует интеграл
,
т.е. существует интеграл
![]() .Тогда
существуют повторные интегралы:
.Тогда
существуют повторные интегралы:
![]() и
и
![]() и имеет место рав-во
и имеет место рав-во
= + . Обратное неверно.
Теорема Тонелли.
Если функция
![]() измерима по мере
и существует хотя бы один из повторных
интегралов
измерима по мере
и существует хотя бы один из повторных
интегралов
![]() ,
тогда функция
интегрируема по мере
и существует двойной интеграл, причем
он равен повторным.
,
тогда функция
интегрируема по мере
и существует двойной интеграл, причем
он равен повторным.
25.Опр-е векторного пр-ва. Алгебр. операции над мн-вами.
Пусть
![]() – поле действительных чисел
или поле комплексных чисел
– поле действительных чисел
или поле комплексных чисел
![]() и будем рассматривать векторные
пространства над этим полем. Это значит,
будем рассматривать:
и будем рассматривать векторные
пространства над этим полем. Это значит,
будем рассматривать:
1)
![]() ;
;
2) операцией умножения
![]()
называется произведение числа на элемент , при этом должны выполняться некоторые свойства:
1. - коммутативная группа относительно сложения.
а) ассоциативность:
![]() ,
,
![]()
существует нейтральный элемент, т.е.
![]()
существует обратный элемент, т.е.
![]()
коммутативность:
![]() ,
,
![]()
2. Аксиома дистрибутивности.
a)
![]()
b)
![]()
c)
![]()
3. Условие нормировки.
![]()
Алгебр операции над мн-вами
Если
![]() и
и
![]() -
два подмножества из векторного
пространства
,
т.е.
-
два подмножества из векторного
пространства
,
т.е.
![]() ,
то определим
,
то определим
![]() .
.
Если одно из этих
множеств является одноточечным, например
![]() ,
то будем писать
,
то будем писать
![]() .
Соответственно, если
.
Соответственно, если
![]() ,
то
,
то
![]() .
.
Аналогично для
умножения. Пусть
![]() .
Определим подмножество
.
Определим подмножество
![]()
Если -одноточечное,
т.е.
![]() ,
то будем писать
,
то будем писать
![]() ,
а если
,
а если
![]() ,
то
,
то
![]() .
.
Пример 1. Рассмотрим
множества
![]() и
и
![]() .
.
Тогда
![]() – открытая правая полуплоскость.
– открытая правая полуплоскость.
Пример 2.
Пусть
![]() ,
тогда
,
тогда
![]() ,
а
,
а
![]() ,
следовательно,
,
следовательно,
![]() .
.
