
- •1.Источники и классификация погрешностей. Неустранимая и вычислительная погрешность.
- •2. Постановка задачи интерполирования. Существование и единственность обобщенного интерполяционного многочлена.
- •3. Интерполяционный многочлен Лагранжа.
- •4. Схема Эйткина
- •5. Остаточный член интерполяционного многочлена Лагранжа.
- •6. Минимиз. Оценки остаточного члена интерпол. Мн-на.
- •7. Разделенные разности и интерполяционная формула Ньютона с разделенными разностями.
- •8. Конечные разности и интерполяционные формулы Ньютона с конечными разностями.
- •9. Составление таблиц.
- •10. Сходимость интерполяционного процесса
- •11.Общая задача интерполирования алгебраическими многочленами. Интерполяционный многочлен Эрмита с узлами кратности 2.
- •13 . Оптимизация шага при численном диф-нии
- •14. Интерполяционные квадратурные формулы
- •15. Квадратурные формулы Ньютона-Котеса
- •16. Простейшие квадрат ф-лы н-Кот. И оценка их погрешности.
- •17. Составные квадратурные формулы средних прямоугольников, трапеций, парабол и оценка их погрешности
- •18. Квадратурные формулы Гаусса
- •20. Метод наименьших квадратов.
- •22.Обобщённые мног-ны наилучших среднеквадратических приближений.
- •24. Многочлены наилучших равномерных приближений. Примеры.
- •25. Наилучшие приближения в линейном нормированном пространстве.
- •26. Интерполяционные сплайны.
- •27. Существование и единственность кубического сплайна.
- •28.Краткие сведения о нормах векторов и матриц.
- •29. Обусловленность линейных алгебраических систем.
- •30. Метод Гаусса решения системы линейных ур-ний.
- •31. - Разложение квадратных матриц.
- •32. Разложение симметричных матриц. Метод квадр. Корней решения лин. Алг.Систем
- •34. Принцип сжимающих отображений в метрическом пространстве.
- •35. Метод простой итерации решения лин. Алг. Систем и усл. Его сходимости.
- •36. Метод Якоби решения линейных алгебраических систем
- •37. Метод Зейделя решения лин. Алг. Систем.
- •38. Метод покоординатного спуска решения линейных алгебраических систем.
- •39. Метод скорейшего спуска решения линейных алгебраических систем
- •40. Степенной метод решения частичной проблемы собственных значений.
- •41. Метод Данилевского раскрытия характеристического уравнения
- •42. Метод вращений решения полной проблемы собственных значений.
- •43. Метод бисекции и простой итерации решения уравнений с одним неизвестным.
- •44. Методы хорд и касательных как частные случаи метода простой итерации.
- •45. Методы локализации корней алгебраического уравнения.
- •46. Метод Лобачевского решения алгебраических уравнений.
- •47. Методы простой итерации и Зейделя решения системы нелинейных уравнений.
- •48. Метод Ньютона и аналоги метода Зейделя решения системы нелинейных уравнений.
- •49. Классификация численных методов решения задачи Коши. Методы Эйлера, трапеций и к-э.
- •50. Метод Рунге-Кутта решения задачи Коши. Построение методов р-к второго порядка точности.
- •51. Оценка погрешности и сходимость одношаговых методов решения задачи Коши.
- •52. Экстраполяц. Метод Адамса решения задачи Коши.
- •53. Интерполяционный метод Адамса решения задачи Коши.
- •54. Общий вид линейных многошаговых методов решения задачи Коши.
- •55. Условие корней многошаговых методов решения задачи Коши
- •56. Сходимость многошаговых методов решения Коши.
- •57. Сеточные методы решения краевых задач для обыкновенных дифференциальных уравнений.
- •58. Сходимость сеточного метода решения краевых задач для обыкновенных диф. Уравнений.
- •59. Методы прогонки и пристрелки решения разностных схем при решении краевых задач для обыкновенных д.У.
- •60. Эквивалентность граничных и вариационных задач
- •61. Метод Ритца решения вариационных задач.
- •62. Построение системы линейных уравнений для определения значений параметров в методе Ритца.
- •63. Вариационно-разностный вариант метода Рица.
- •64. Сеточные методы решения краевой задачи для уравнения Пуассона. Фоpмулиpовка исходной диффеpенциальной краевой задачи
- •Постpоение pазностной схемы
- •65. Основные понятия теории разностных схем.
- •66. Сходимость сеточного метода
- •Фоpмулиpовка исходной дифференциальной краевой задачи
- •67.Метод матричной прогонки решения разностной схемы. Фоpмулиpовка исходной диффеpенциальной краевой задачи
- •68. Разностные схемы для одномерного параболического уравнения. Фоpмулиpовка исходной диффеpенциальной задачи
- •69. Разностные схемы решения задачи Коши для уравнения гиперболического типа.
- •70. Сеточные методы решения смешанной задачи для уравнений гиперболического типа.
- •71. Метод квадратур решения интегрального уравнения Фредгольма 2-го рода.
- •72. Решение интегрального уравнения Фредгольма 2-го рода с вырожденным ядром.
- •Решение интегр. Ур-ния с вырожденным ядром.
- •73. Решение интегрального уравнения Фредгольма 2-го рода методом вырожденного ядра.
- •Способы приближения невырожденного ядра вырожденным.
58. Сходимость сеточного метода решения краевых задач для обыкновенных диф. Уравнений.
Для
граничной задачи
 ,
(1)
y(a)=A,
y(b)=B
(2)
на равномерной сетке xi=a+ih,
i=0,1,...,N;h=(b-a)/N
построена разностная схема
,
(1)
y(a)=A,
y(b)=B
(2)
на равномерной сетке xi=a+ih,
i=0,1,...,N;h=(b-a)/N
построена разностная схема
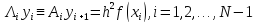 ,(3)
y0=A,
yN=B
(4).
Точное решение y(x)
в узлах сетки:
,(3)
y0=A,
yN=B
(4).
Точное решение y(x)
в узлах сетки:
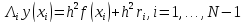 ,(5)
,(5)
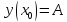 ,y(xN)=B
(6).
Для погрешности, с которой алгебраические
уравнения (3) приближают диф-ое уравнение
(1) в узлах сетки, была получена оценка
,y(xN)=B
(6).
Для погрешности, с которой алгебраические
уравнения (3) приближают диф-ое уравнение
(1) в узлах сетки, была получена оценка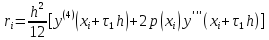 (7).
Граничные условия приближаются точно.
Фактическое решение
(7).
Граничные условия приближаются точно.
Фактическое решение
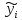 системы (3), (4), вследствие выч-ой
погрешности, отличается от точного
решенияyi
этой системы, =>
системы (3), (4), вследствие выч-ой
погрешности, отличается от точного
решенияyi
этой системы, =>
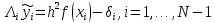 ,(8)
,(8)
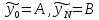 (9)
Оценим погрешности
(9)
Оценим погрешности
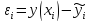 .
Вычитая из (5), (6) соотв. ур-ния (8), (9),
получим разностную задачу
.
Вычитая из (5), (6) соотв. ур-ния (8), (9),
получим разностную задачу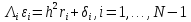 ,(10)
,(10)
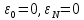 (11).
(11).
Лемма.
Пусть выполняются условия:1)
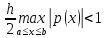 2)g(x)≤0,a≤x≤b
3)
2)g(x)≤0,a≤x≤b
3)
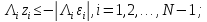 4)
4) ,
для произвольных последовательностей
,
для произвольных последовательностей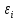 ,
,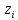 .Тогда
.Тогда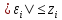 ,
i=0,1,...N.
Док-во.
Рассмотрим 2 числовые последовательности
zi±εi,
i=0,1,...,N.
Из условия 3) леммы имеем
,
i=0,1,...N.
Док-во.
Рассмотрим 2 числовые последовательности
zi±εi,
i=0,1,...,N.
Из условия 3) леммы имеем
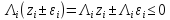 ,i=1,2...N-1.
В силу принципа max
для оператора
,i=1,2...N-1.
В силу принципа max
для оператора
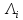 последоват-тиzi±εi,i=0,1,...N
принимают свое наименьшее отрицательное
значение на границе. Из условия (4) на
границе имеем z0±ε0≥0
и zN±εN≥0.
Т.о. zi±εi≥0,
i=0,1,...N
лемма доказана.
последоват-тиzi±εi,i=0,1,...N
принимают свое наименьшее отрицательное
значение на границе. Из условия (4) на
границе имеем z0±ε0≥0
и zN±εN≥0.
Т.о. zi±εi≥0,
i=0,1,...N
лемма доказана.
Построим
посл-ть zi.
Рассм. граничную задачу:
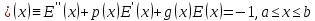 ,(12)
,(12)
E(a)=0,E(b)=0
(13) При a<x<b
решение E(x)
этой задачи положительно: E(x)>0.
Докажем это от противного. Пусть
существует такое
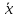 ,
что
,
что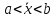 и
и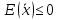 .
Тогда внутри отрезка найдется точка
.
Тогда внутри отрезка найдется точка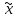 ,
в которой достигается неположит-ыйmin:
,
в которой достигается неположит-ыйmin:
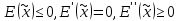 .
В результате противоречие
.
В результате противоречие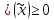 .
Для последов-ти
.
Для последов-ти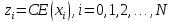 выполняются условия 4) леммы сравнения
при любой положительной константеC.
Найдем значение константы C,
при котором будут выполнены условия
3). Из (10) и (7) имеем
выполняются условия 4) леммы сравнения
при любой положительной константеC.
Найдем значение константы C,
при котором будут выполнены условия
3). Из (10) и (7) имеем
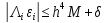 ,
или
,
или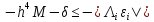 (14),
где
(14),
где
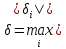 ,
,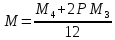 ,
,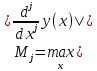 ,
,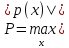 .
Из
.
Из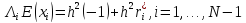 получим при достаточно маломh
получим при достаточно маломh
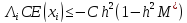 ,
,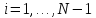 ,(15),
где
,(15),
где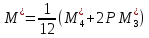 ,
,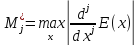 .
Из (14) и (15) следует, что для вып. усл. 3)
леммы сравн. полож. константыC
должно удовлетворять неравенству
.
Из (14) и (15) следует, что для вып. усл. 3)
леммы сравн. полож. константыC
должно удовлетворять неравенству
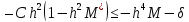 .
=> получ.
.
=> получ.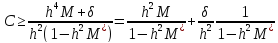 .Использ. лемму сравнения, приходим к
искомой оценке
.Использ. лемму сравнения, приходим к
искомой оценке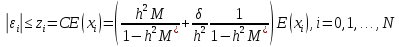 (16) Из оценки (16) вытекает, что решение
(16) Из оценки (16) вытекает, что решение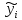 системы (8), (9) приh→0
равномерно сходится к решению y(x)
исходной задачи (1), (2), если δ/h2→0
при h→0.
системы (8), (9) приh→0
равномерно сходится к решению y(x)
исходной задачи (1), (2), если δ/h2→0
при h→0.
59. Методы прогонки и пристрелки решения разностных схем при решении краевых задач для обыкновенных д.У.
Для
гран. задачи
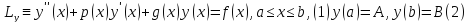 на равномерной сетке
на равномерной сетке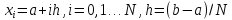 была построена разностная схема
была построена разностная схема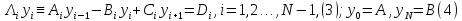 .
Коэффициенты в уpавнениях (3):
.
Коэффициенты в уpавнениях (3):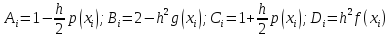 (5).
Метод
разностной пристрелки.
(3) можно решить относительно
(5).
Метод
разностной пристрелки.
(3) можно решить относительно
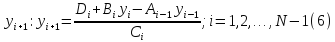 Так как
Так как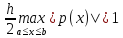 ,
то
,
то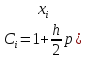 )>0
и операция деления в (6) реализуется.
Последовательность, образуемая по
правилу (6) однозначно определяется
значениями первых двух своих членов:
)>0
и операция деления в (6) реализуется.
Последовательность, образуемая по
правилу (6) однозначно определяется
значениями первых двух своих членов: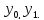 Постpоим последоват-ти
Постpоим последоват-ти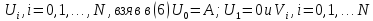 взяв в (6)
взяв в (6)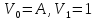 Очевидно, последоват-ть
Очевидно, последоват-ть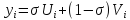 ,i=0,1…N
,i=0,1…N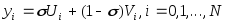 (7)
при любом значении паpаметpа σ
удовлетворяет сис-ме (3) и левому граничному
условию
(7)
при любом значении паpаметpа σ
удовлетворяет сис-ме (3) и левому граничному
условию
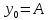 .
Чтобы выполнялось пpавое гpаничное
условие
.
Чтобы выполнялось пpавое гpаничное
условие ,
нужно взять
,
нужно взять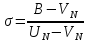 (8)
(8)
Метод
разностной прогонки.
Уравнение
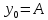 можем записать:
можем записать: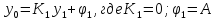 Пусть мы выpазили
Пусть мы выpазили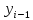 через
через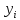 фоpмулой
фоpмулой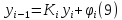 Подставим это для
Подставим это для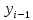 в (3):
в (3): -
-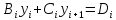 .
Отсюда находим
.
Отсюда находим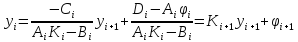 Т.о. коэффициенты в (9)
Т.о. коэффициенты в (9)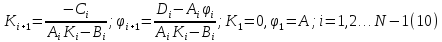 После этого из (9) пpи i=N имеем
После этого из (9) пpи i=N имеем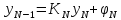 .
По фоpмуле (9) пpи i=N,N-1…2 последовательно
вычисляем
.
По фоpмуле (9) пpи i=N,N-1…2 последовательно
вычисляем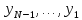 .
Гpаничные значения
.
Гpаничные значения даны. Данный метод решения граничной
задачи - метод пpогонки. Вычисления по
(10) - прямой ход прогонки, а по (9) –
обратный.Теорема.
В расчетных формулах (10) знаменатели не
обращаются в нуль. Доказательство.
Задано
даны. Данный метод решения граничной
задачи - метод пpогонки. Вычисления по
(10) - прямой ход прогонки, а по (9) –
обратный.Теорема.
В расчетных формулах (10) знаменатели не
обращаются в нуль. Доказательство.
Задано
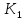 =0.
Пусть
=0.
Пусть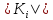 <1,
тогда |
<1,
тогда |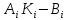 |=
|=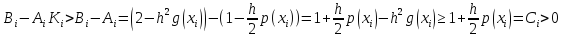 .
Далее
.
Далее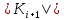 =|
=|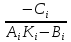 |<1.
Утверждение теоремы доказано. Т.к.
|<1.
Утверждение теоремы доказано. Т.к.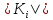 <1,
вычисления по формуле (9) будут устойчивы
к вычислению погрешности. Исследуем
устойчивость к вычислению погрешности
формулы (10) к φi.
Цепочка преобразований:
<1,
вычисления по формуле (9) будут устойчивы
к вычислению погрешности. Исследуем
устойчивость к вычислению погрешности
формулы (10) к φi.
Цепочка преобразований:
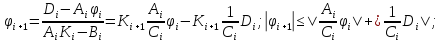
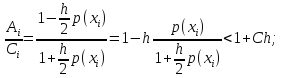
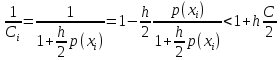 ;
;
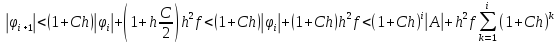
тут
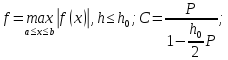
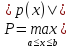 .
Учитывая
.
Учитывая
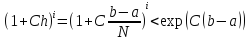 при 0≤i≤N оценка
при 0≤i≤N оценка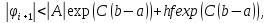 Т.о. на прямом ходе прогонки по (10) при
Т.о. на прямом ходе прогонки по (10) при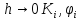 ограниченые, =>устойчивы к вычислительной
погрешности.
ограниченые, =>устойчивы к вычислительной
погрешности.
