
- •1.Расстояние между двумя точками. Деление отрезка в данном отношении.
- •7.Угол между 2-мя прямыми. Условия параллельности и перпендикулярности.
- •14. Угол между 2-мя векторами.
- •8. Кривые второго порядка (эллипс, парабола, гипербола)
- •10. Проекция вектора на ось
- •12.Операции над векторами:
- •19. Решение методом Крамера
- •20. Линейная зависимость векторов. Базис и ранг системы векторов. Разложение вектора по данному базису.
- •21. Матрица и её экономический смысл. Операции над матрицами.
- •22. Ранг матрицы. Эквивалентные матрицы. Вычисление ранга матрицы методом Гаусса.
- •23. Обратная матрица и её вычисления.
- •25. Система линейных алгебраических уравнений относительно n неизвестных. Решение системы методом Гаусса. Понятие базисного решения.
- •27. Понятие функции. Область определения. Различные способы задания.
- •28.Числовая последовательность. Определение предела числовой последовательности.
- •29.Определение бесконечно большой и бесконечно малой последовательности. Связь между ними. Операции над бесконечно малыми последовательностями.
- •30.Предел функции в точке. Односторонние пределы.
- •34. Точки разрыва и их классификация.
- •35. Производная ф-ции. Гео. И эк. Смысл.
- •36. Произв. Сложной и обр. Ф-ции. Табл. Производных.
- •42. Экстремум ф-ции и его необходимое условие. Достаточные признаки экст.
- •46.Экстремум функции нескольких переменных. Необходимое условие экстремума
- •47.Метод наименьших квадратов
- •48.Первообразная функции. Неопределённый интеграл. Основные свойства неопределённого интеграла
- •49.Замена переменной (подстановка) в неопределённом интеграле. Интегрирование по частям.
- •51.Интегрирование выражений, содержащих тригонометрические функции.
- •52. Интегрирование некоторых иррациональных функций.
- •53.Геометрическая задача, приводящая к понятию определённого интеграла. Определённый интеграл. Его свойства.
- •54. Применение определённого интеграла в экономике.
- •Теорема
- •Формула Ньютона – Лейбница связывает неопределенный и определенный интегралы.
- •56.Замена переменной и интегрирование по частям в определенном интеграле. Метод замены переменной
- •57.Площадь плоской фигуры. Объем тела вращения.
- •58 Интегралы с бесконечными пределами:
- •59.Интегралы от неограниченнх ф-ий
- •60.Дифференциальные уравнения (основные понятия)
- •64. Производственная функция Кобба-Дугласа:
- •66.Признаки срав-ия для полож. Рядов. Пр. Даламбера и Коши сход-ти рядов.
- •67.Знакопеременные ряды. Абсолютная и условная сходимость.
- •68.Знакочередующиеся ряды.Признак Лейбница.
- •69.Понятие степенного ряда .Область сходимости степенного ряда
- •70. Ряды Тейлора и Маклорена.
51.Интегрирование выражений, содержащих тригонометрические функции.
1.Метод подведения под знак диф. Заключается в том, что некоторые сомножетели подинтегральной функции подводятся под знак диф, после чего используется подходящий табличный интеграл.2.Интегралы вида ∫ sin mx cos nx dx; ∫sin mx sin nx dx;
∫ cos mx cos nx dx применяются следующие формулы: sin mx cos nx= ½ (sibn (m+n)x+sin(m-n)x); sin mx sin nx= ½(cos(m-n)x-cos(m+n)x); cos mx cos nx=1/2(cos(m-n)x+cos(m+n)x).3.Интегралы вида:∫ cosmx sinnx dx интегрируются следующим образом:Если оба числа m и n– чётные, то пользуемся формулой понижения степени cos2x=(1+cosx)/2; sin2x=(1-cos2x)/2; sinx cosx=sin2x/2
52. Интегрирование некоторых иррациональных функций.
Неопределённый
интеграл ![]() выделением полного квадрата в подкоренном
выражении и введением новой переменной
выделением полного квадрата в подкоренном
выражении и введением новой переменной
![]() в зависимости от знака
в зависимости от знака ![]() приводится к одному из интегралов:
приводится к одному из интегралов:
![]()
![]()
Неопр. интеграл
![]() завис. от знака
завис. от знака ![]() приводится к одному из интегралов:
приводится к одному из интегралов:
![]()
![]()
Неопр.![]() в завис. от знака
в завис. от знака ![]() приводится к одному из интегралов:
приводится к одному из интегралов:
![]()
![]()
Интеграл вида
![]() ,
где R-
рациональная ф-я и
,
где R-
рациональная ф-я и ![]() целые числа, с помощью подстановки
целые числа, с помощью подстановки ![]() , где n-наименьшее
общее кратное чисел
, где n-наименьшее
общее кратное чисел ![]() ,
приводится к интегралу от рациональной
ф-и.
,
приводится к интегралу от рациональной
ф-и.
Интеграл дифференциального бинома
![]()
где n,m,p- рац. числа ; a,b- постоянные. отличные от нуля, сводится к интегралу от рац. ф-и в трёх случаях:
1)котда p-целое
число, -разложением на слагаемые по
формуле бинома Ньютона при ![]() ;
подстановкой
;
подстановкой ![]() ,
где N-
общий знаменатель дробей m
и n;
,
где N-
общий знаменатель дробей m
и n;
2)когда![]() - целое число, - подстановкой
- целое число, - подстановкой ![]() , где s-
знаменатель дроби p;
, где s-
знаменатель дроби p;
3)когда ![]() - целое число, - подстановкой
- целое число, - подстановкой ![]()
53.Геометрическая задача, приводящая к понятию определённого интеграла. Определённый интеграл. Его свойства.
Пусть ф-я ![]() определена на отрезке
определена на отрезке ![]() .
Разобьём отрезок
.
Разобьём отрезок![]() точками
точками ![]() .
Длина каждого
.
Длина каждого ![]() .
Выберем в каждом из частичных отрезков
точку
.
Выберем в каждом из частичных отрезков
точку ![]() .
.
Рассмотрим сумму
![]() Эта
сумма наз. частично интегральной суммой
ф-и
Эта
сумма наз. частично интегральной суммой
ф-и ![]() на отрезке
на отрезке![]() .
Геометрически сумма
.
Геометрически сумма ![]() предст. собой алгебраич. сумму площадей
прямоугольников, в основании кот. лежат
отрезки
предст. собой алгебраич. сумму площадей
прямоугольников, в основании кот. лежат
отрезки ![]() ,
а высоты равны
,
а высоты равны ![]() .
.
Предел интегральной
суммы ![]() ,
найденный при условии, что длина
наибольшего частичного отрезка стрем.
к 0, ( мелкость разбиения стрем. к 0 ) наз.
определённым интегралом функции
,
найденный при условии, что длина
наибольшего частичного отрезка стрем.
к 0, ( мелкость разбиения стрем. к 0 ) наз.
определённым интегралом функции ![]() в пределах от
в пределах от ![]() до
до ![]()
![]()
Теорема: если ф-я
![]() непрерывна на
непрерывна на ![]() ,
то она интегрируема на
,
то она интегрируема на ![]() ,
т.е. предел интегральной суммы существует
и не зависит от способа разбиения отрезка
,
т.е. предел интегральной суммы существует
и не зависит от способа разбиения отрезка
![]() на частичные отрезки
на частичные отрезки ![]() и выбора на них точек
и выбора на них точек ![]() .
.
Если ![]() на
на![]() ,
то геометрически опр. интеграл выражает
площадь фигуры, ограниченной графиком
,
то геометрически опр. интеграл выражает
площадь фигуры, ограниченной графиком
![]() ,
осью ОХ и двумя прямыми
,
осью ОХ и двумя прямыми ![]() и
и ![]() , называемый криволинейной трапецией.
, называемый криволинейной трапецией.
Свойства определённого интеграла:



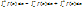
 ,
то
,
то


 ,
,  ,
то
,
то 
 ф-я
ф-я
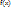 непрерывна на отрезке
непрерывна на отрезке ,
,
 ,то
на этом отрезке сущ. хотя бы одна точка
,то
на этом отрезке сущ. хотя бы одна точка
 ,
,
 такая,
что
такая,
что 
 −я
−я
 непрерывна
и
непрерывна
и ,то
имеет место равенство
,то
имеет место равенство  Ф-я
Ф-я  наз.
определённым интегралом с переменным
верхним пределом.
наз.
определённым интегралом с переменным
верхним пределом. Ньютона-Лейбница:
если
Ньютона-Лейбница:
если  -
какая-либо первообразная от
-
какая-либо первообразная от ,
то
,
то 
