Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МИЭТ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

bdz_teorver

.pdf

Скачиваний:

414

Добавлен:

05.06.2015

Размер:

771.45 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 126 7 8 9 10 11 12 > Следующая >>>

Условие задачи

Каждый поступающий в университет должен сдать три экзамена.

Вероятность успешной сдачи первого экзамена равна 0,6, второго –

0,7, третьего – 0,9.

Следующий экзамен поступающий сдает только в случае успешной сдачи предыдущего.

Случайная величина X – число экзаменов,

сдававшихся поступающим в университет.

Вариант

X 2

Вариант

X 2 − 3

Вариант

PDF created with pdfFactory Pro trial version www.pdffactory.com

Условие задачи

Студент разыскивает нужную ему формулу,

заказав в читальном зале библиотеки три справочника.

Вероятность того, что

формула есть в первом справочнике, равна

0,7, во втором – 0,8, в

третьем – 0,9. Случайная величина X

–количество справочников, в

которых содержится нужная студенту формула.

Имеется пять однотипных ключей.

Из них только один подходит к замку. Случайная величина X

–число попыток открывания замка (испробованный ключ

в последующих попытках не участвует).

Вариант

X 2 − 3

Вариант

X 2

Вариант

+ 5 29

X 2 + 3

PDF created with pdfFactory Pro trial version www.pdffactory.com

Условие задачи

Вариант

На

шахматную

доску 24

2 X

X 2 − 5

ставится

слон.

Случайная величина X

–

число

клеток,

которые

стоят

под

ударом этого слона.

З а д а н и е 3.8.

Случайная

величина

является

непрерывной.

Найти

плотность

распределения

fY ( y) случайной величины Y (табл.3.5).

Таблица 3.5

Условие задачи		Вариант	Y
Условие задачи			Y

Случайная		1	1
величина	X			X
величина	X
распределена	по
показательному
закону	с
параметром λ = 2 .
Случайная		2		X 3 + 5
величина	X
распределена
нормально	с
параметрами m = 0
и σ = 1.
Случайная		3	2 − X 3
величина	X
распределена
равномерно	на
отрезке [0;1].
Случайная		4	1− X 5
величина X имеет

Вариант

− X2

3X −1

e− X

Вариант

X 5 +1

2eX

ln(X + 2)

5X −1

PDF created with pdfFactory Pro trial version www.pdffactory.com

Условие задачи				Вариант	Y	Вариант	Y		Вариант	Y
плотность				Вариант		Вариант			Вариант
плотность
распределения
f X (x) =	ì2x,	x Î[0;1],
f X (x) =	í	x	Ï[0;1].
	î 0,	x	Ï[0;1].
Случайная				5	X 3 + 2	12	1		19	3ln X
величина				X			X
величина				X
распределена				по
показательному
закону				с
параметром λ = 1 .
Случайная				6	2 3 X	13	-	1	20	e− X
							-	X
величина				X				X
величина				X
распределена				по
закону	Коши			с
плотностью
fX (x) =	1
fX (x) =	p(1+ x2 ) .
	p(1+ x2 ) .
Случайная				7	1− X 5	14	arctg X		21	3 X +1
величина				X
распределена
нормально				с
параметрами			m = 1
и σ = 2 .
Случайная				22	X 5 − 2	25	-	4	28	3X
величина				X			-	X
величина				X
распределена				по
показательному
закону				с
параметром λ = 3 .
Случайная				23	1− X 3	26	3 5 X		29	arctg(X -1)
величина				X
распределена				на
					54

PDF created with pdfFactory Pro trial version www.pdffactory.com

Условие задачи

Вариант

всей числовой оси

с плотностью

(x) = 0,5e− |x|

Случайная

2e− X

X 3 - 5

величина

распределена

по

закону

Рэлея

плотностью

−

2 , x

> 0,

(x) = íxe

0, x

£ 0.

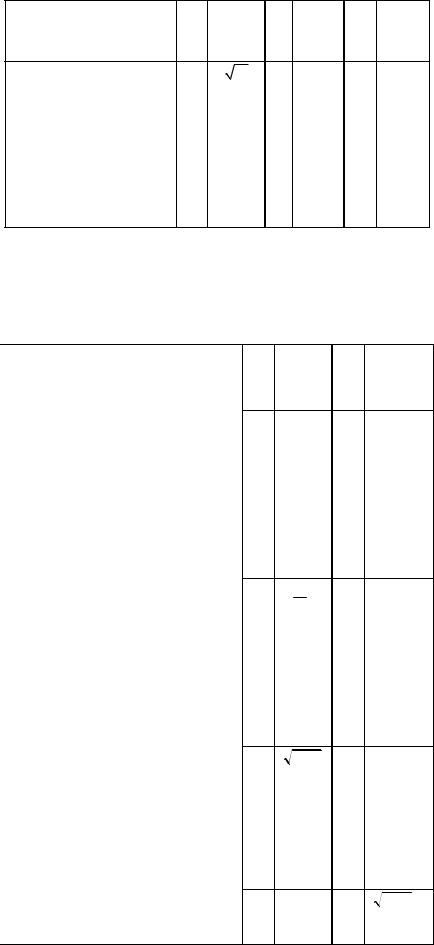
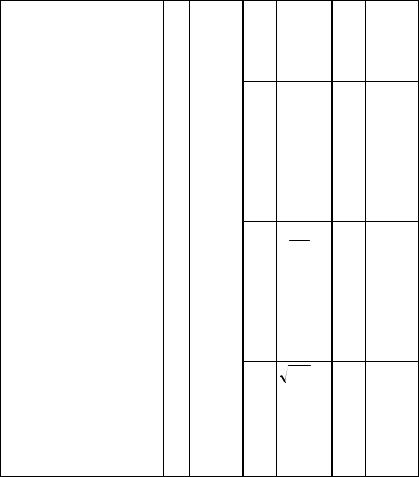
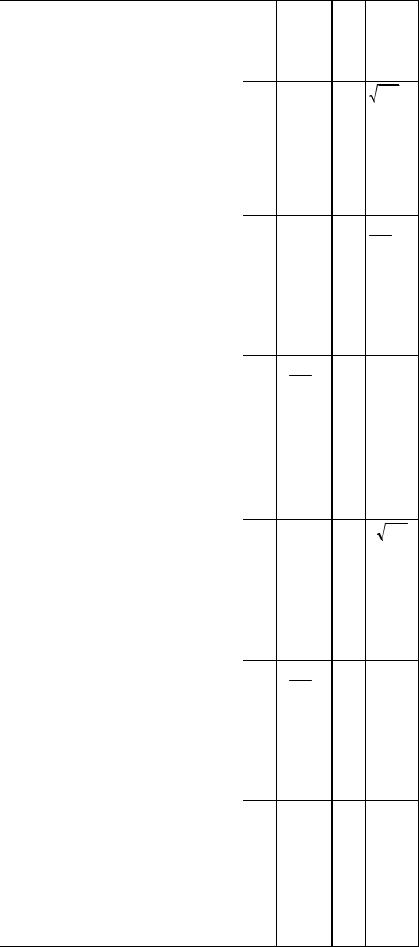
З а д а н и е 3.9. Случайная величина X является непрерывной. Найти плотность распределения fY ( y) случайной величины Y (табл.3.6).

Таблица 3.6


Условие задачи				Вариант	Y
Условие задачи					Y

Случайная		величина		1	1
X	распределена		по			X 2
X	распределена		по
показательному
закону с параметром
λ = 2 .
Случайная		величина		4		X 2 + 5
X	распределена
нормально			с
параметрами m = 0			и
σ = 1.
Случайная		величина		5	\| X \| - 2

X распределена

равномерно на отрезке [0;1].

Вариант

2|X |

- X24

3| X |

Вариант

X 2 +1

2e|X |

2 − X 2

PDF created with pdfFactory Pro trial version www.pdffactory.com

Условие задачи								Вариант	Y	Вариант
Условие задачи									Y
										13
Случайная					величина			6	1− X 4	13
X		имеет			плотность
распределения
			ì2x,		x Î[0;1],
f X (x) = í					x Ï[0;1].
			î 0,		x Ï[0;1].
										14
Случайная					величина			7	X 4 + 2	14
X		распределена					по
показательному
закону с параметром
λ = 1 .
										15
Случайная					величина			8	\| X \| + 2	15
X		распределена					по
закону					Коши		с
плотностью
fX		(x) =		1
fX		(x) =	p(1	+ x2 ) .
			p(1	+ x2 ) .
Случайная					величина			9	1− X 4	16
X			распределена
нормально							с
параметрами m = 1							и
σ = 2 .
										17
Случайная					величина			10	X 2 + 4	17
X		распределена					по
показательному
закону с параметром
λ = 3 .
										27
Случайная					величина			25	1− X 2	27
X		распределена					на
всей числовой оси с
плотностью
f	X	(x) = 0,5e− \|x\|				.
	X					.

									56

e−|X |

ln | X |

− | X1 |

-ln | X |

−| X4 |

| X | -1

Вариант

5| X |

| X |

2e−|X |

−3| X |

3|X |

5ln | X |

PDF created with pdfFactory Pro trial version www.pdffactory.com

Условие задачи

Вариант

Случайная

величина

−1

3e−|X |

X распределена

по

X |

закону

Рэлея

плотностью

−

2 , x > 0,

fX (x) = íxe

x £ 0.

PDF created with pdfFactory Pro trial version www.pdffactory.com

Вариант

X 4 - 5

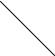
4. Системы случайных величин (случайные векторы)

З а д а н и е 4.1. Случайный вектор (X ; Y ) имеет распределение:

Y	–1	0	b
X

a	p	0,15	0,05

0	0,05	0,2	q

1	с	0,15	0,1

Учитывая данные, представленные в							табл. 4.1, найти с,				центр рассеивания (mX ; mY ) ,
коэффициент корреляции			ρX ,Y		. Вычислить вероятность					P{X < Y}		.
коэффициент корреляции					. Вычислить вероятность							.
														Таблица 4.1

	Вариант	a		b		p	q	Вариант	a		b	p	q

	1	–1		1		0	0	16	–3		1	0,1	0,1

	2	–2		2		0,1	0,1	17	–3		2	0,1	0,2

	3	–2		1		0,1	0,2	18	–3		5	0,3	0

	4	–1		4		0,3	0	19	–3		6	0	0,3

	5	–1		1		0	0,3	20	–2		4	0	0,2

	6	–2		2		0	0,2	21	–5		5	0,1	0

	7	–2		1		0,1	0	22	–5		5	0,2	0,1

	8	–1		1		0,2	0,1	23	–4		5	0,1	0,1

	9	–2		2		0,1	0,2	24	–4		6	0,1	0,2

	10	–2		1		0,3	0	25	–4		4	0,3	0

	11	–1		1		0	0,3	26	–2		1	0	0

	12	–2		2		0	0	27	–2		2	0,05	0,15

	13	–2		1		0,3	0	28	–2		1	0,05	0,15

	14	–3		4		0	0,3	29	–3		4	0,05	0,15

	15	–1		2		0	0	30	–2		3	0	0

PDF created with pdfFactory Pro trial version www.pdffactory.com

За д а н и е 4.2. Решить задачу.

1.Игральная кость подбрасывается до первого выпадения числа 6, но не более трех раз. Случайные величины: Х – число выпадений «шестерки», Y – число

подбрасываний. Описать закон распределения случайного вектора (X ; Y ) . Найти

одномерные законы распределения компонент X и Y. Вычислить вероятность

P{X < Y} . Построить совместную функцию распределения и вычислить ее значение

в точке (0,5; 4) .

2.Игральная кость подбрасывается до первого выпадения числа 6, но не более трех раз. Случайные величины: Х – число выпадений «шестерки», Y – число подбрасываний. Описать закон распределения случайного вектора (X ; Y ) . Найти центр рассеивания и коэффициент корреляции.

3.	Монета	подбрасывается	до	первого	выпадения	цифры,	но
	не более четырех раз. Случайные величины: Х – число выпадений «герба», Y –
	число подбрасываний. Описать закон распределения случайного вектора (X ; Y ) .
	Найти одномерные законы распределения компонент X и Y. Вычислить
	вероятность	P{X < Y} . Построить		совместную	функцию	распределения	и
	вычислить ее значение в точке (0,5; 4) .
4.	Монета	подбрасывается	до	первого	выпадения	цифры,	но
	не более четырех раз. Случайные величины: Х – число выпадений «герба», Y –
	число подбрасываний. Описать закон распределения случайного вектора (X ; Y ) .
	Найти центр рассеивания и коэффициент корреляции.

5.Стрелок стреляет по мишени из пистолета до первого попадания, но не более трех раз. Вероятность попадания в мишень при каждом выстреле равна 0,8. Случайные величины: Х – модуль разности между числом попаданий и числом промахов, Y –

число промахов. Описать закон распределения случайного вектора (X ; Y ) . Найти одномерные законы распределения компонент X и Y. Вычислить вероятность

P{X = Y}. Построить совместную функцию распределения и вычислить ее значение

в точке (0,5; 4) .

6.Стрелок стреляет по мишени из пистолета до первого попадания, но не более трех раз. Вероятность попадания в мишень при каждом выстреле равна 0,8. Случайные величины: Х – модуль разности между числом попаданий и числом промахов, Y –

число промахов. Описать закон распределения случайного вектора (X ; Y ) . Найти центр рассеивания и коэффициент корреляции.

PDF created with pdfFactory Pro trial version www.pdffactory.com

7.Игральная кость подбрасывается три раза. Случайные величины: Х – число появлений «шестерки», Y – число появлений четной цифры. Описать закон распределения случайного вектора (X ; Y ) . Найти одномерные законы распределения компонент X и Y. Вычислить вероятность P{X = Y}. Построить совместную функцию распределения и вычислить ее значение в точке (0,5; 4) .

8.Игральная кость подбрасывается три раза. Случайные величины: Х – число появлений «шестерки», Y – число появлений четной цифры. Описать закон распределения случайного вектора (X ; Y ) . Найти центр рассеивания и коэффициент корреляции.

9.Число Х выбирается из множества целых чисел {1; 2; 3; 4} . Затем из этого множества выбирается наудачу число Y, меньшее первого числа. Описать закон распределения

случайного вектора (X ; Y ) . Найти одномерные законы распределения компонент X

и Y. Вычислить вероятность P{X > Y}. Построить совместную функцию распределения и вычислить ее значение в точке (3,5; 3) .

10.Число Х выбирается из множества целых чисел {1; 2; 3; 4} . Затем из этого множества выбирается наудачу число Y, меньшее первого числа. Описать закон распределения случайного вектора (X ; Y ) . Найти центр рассеивания и коэффициент корреляции.

11.Иван и Петр наудачу извлекают по одному шару из урны, содержащей 3 белых и 5 черных шаров. Иван извлекает шар первым. Случайные величины: X – число черных шаров у Ивана, Y – число белых шаров у Петра. Описать закон распределения случайного вектора (X ; Y ) , если выбор шаров производится без возвращения. Найти одномерные законы распределения компонент X и Y.

Построить совместную функцию распределения и вычислить ее значение в точке

(0,5; 4) . Вычислить вероятность P{X < Y} .

12.Иван и Петр наудачу извлекают по одному шару из урны, содержащей 3 белых и 5 черных шаров. Иван извлекает шар первым. Случайные величины: X – число черных шаров у Ивана, Y – число белых шаров у Петра. Описать закон распределения случайного вектора (X ; Y ) , если выбор шаров производится без возвращения. Найти центр рассеивания и коэффициент корреляции.

13.Иван и Петр наудачу извлекают по одному шару из урны, содержащей 3 белых и 5 черных шаров. Случайные величины: X – число белых шаров у Ивана, Y – число черных шаров у Петра. Описать закон распределения случайного вектора (X ; Y ) ,

PDF created with pdfFactory Pro trial version www.pdffactory.com

<<< < Предыдущая 1 2 3 4 56 / 126 7 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
27.03.2016135.73 Кб10bdz_1_mp_14_2015-09-11.pdf
#
27.03.2016120.02 Кб14bdz_2_mp_10_2015-10-29.pdf
#
05.06.2015145.28 Кб13bdz_3mp_13.pdf
#
05.06.2015146.57 Кб7bdz_5_mp_12.pdf
#
05.06.2015739.2 Кб190BDZ_linal_matan.pdf
#
05.06.2015771.45 Кб414bdz_teorver.pdf
#
23.09.201958.38 Кб0Bil_Sety(new).docx
#
16.08.2019123.22 Кб4bla_blatov_2_1.docx
#
27.03.2016208.45 Кб5buklet_2015_god.docx
#
17.12.2018337.92 Кб4C1.doc
#
22.12.2018189.95 Кб3C2.doc