
Строительная механика
.pdf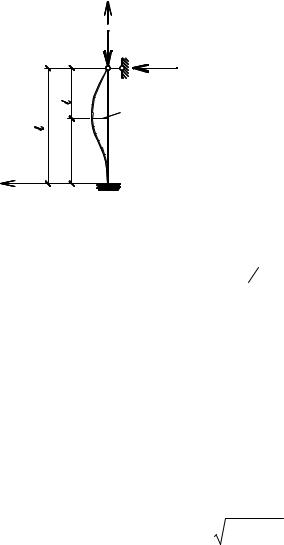
-x
x |
|
PКР |
Rв |
|
|
B |
|
y(x) |
|
При бесконечно малых перемещениях можно принять, что положение изогнутой оси стержня описывается приближенно дифференциальным уравнением:
|
x |
y |
0 А |
Рис. 5.10
|
|
− EI |
d 2 y |
= M x |
(5.4) |
|
|
dx2 |
|||
|
|
|
|
|
|
|
|
вместо точного |
|
||
− EI |
y′′ |
= M x . |
|
(5.4,а) |
|
[1 + (y′)2 ]32 |
|
||||
Изгибающий момент в произвольном сечении стержня
M x = Pкр y − RB (l− x).
С учетом принятого направления координатных осей дифференциальное уравнение изгиба по условию (5.4) получаем в виде:
EIy′′ + Pкр y = RB (l − x).
Разделив все слагаемые на EI и обозначив
|
|
|
|
n = |
|
Pкр / EI , |
(а) |
||
|
|
′′ |
|
2 |
|
RB |
|
|
|
получаем: |
y |
+ n |
|
y = |
EI (l − x). |
|
|||
|
|
|
|||||||
Решение этого неоднородного дифференциального уравнения будет: |
|||||||||
|
|
|
y = Asin(nx)+ B cos(nx)+ C(l− x), |
(5.5) |
|||||
где A, B и C – постоянные интегрирования. |
|
||||||||
Так как по условию (а) |
|
|
|
|
|
|
|||
|
|
|
|
|
P |
|
= n2 EI, |
(5.6) |
|
|
|
|
|
|
кр |
|
|
|
|
то критическая нагрузка может быть найдена, если известен параметр « n ». Для определения постоянных A, B и C в уравнении (5.5) воспользуем-
ся кинематическими граничными условиями:
1) При x = 0, y = 0; 2) При x = 0, y′ = 0; 3) При x = l, y = 0.
81

По первому условию y = A 0 + B 1+C l = 0. |
(1) |
||
По второму условию y′ = A n cos(nx)− B n sin(nx)− C = 0 . |
|
||
При x = 0 |
y′ = A n 1 − B 0 − C 1 = 0 . |
(2) |
|
По третьему условию y = A sin(nl)+ B cos(nl)+ C 0 = 0 . |
(3) |
||
Система однородных уравнений имеет вид: |
|
||
|
A 0 + B 1 |
+ C l = 0; |
|
|
|
− C 1 = 0; |
(5.7) |
|
A n − B 0 |
||
|
|
|
|
|
A sin(nl)+ B cos(nl)+ C 0 = 0. |
|
|
Уравнения (5.7) удовлетворяются, если A = B = C = 0, но это условие |
|||
соответствует недеформированному состоянию системы. Если A, |
B и C от- |
||
личны от нуля, то должно выполняться условие (5.3). Этому случаю соответствуют неопределенные значения постоянных, что характеризует безразличное состояние системы. Таким образом, уравнение устойчивости имеет вид:
|
|
0 |
1 |
l |
|
|
|
|
|||||
D = |
|
n |
0 |
−1 |
|
= 0 . |
|
|
sin(nl) |
cos(nl) |
0 |
|
|
Раскрыв определитель, имеем
nl cos(nl)−1 sin(nl)= 0 ,
или tg(nl)= nl . (5.8)
Чтобы найти наименьшее (отличное от нуля) значение критической силы, нужно отыскать наименьший положительный корень уравнения (5.8). В общем случае такого типа уравнения решаются способом последовательных приближений. Путем подбора находим nl = 4,493 и по формуле (5.6)
P = n2 EI = 20,19EI .
кр |
l 2 |
|
82

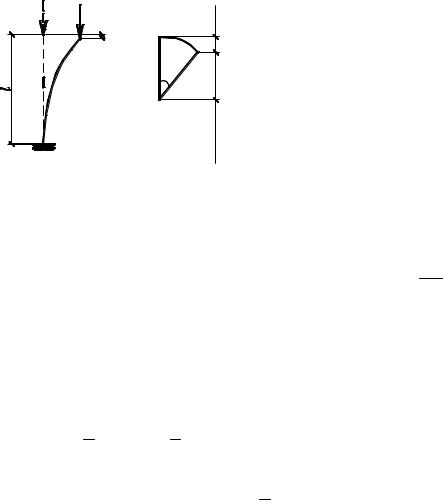
Для упругой центрально нагружен-
|
|
x |
|
ной шарнирно опертой стойки посто- |
||
|
|
|
|
|||
|
|
PКР |
|
янного сечения (рис. 5.11) определе- |
||
|
|
|
|
|||
|
|
|
|
ние критической нагрузки статиче- |
||
|
EI |
y(x) |
|
ским методом повторит предыдущий |
||
|
|
|
||||
|
x |
|
|
расчет. Приняв |
дифференциальное |
|
y |
0 |
|
|
уравнение |
по |
зависимости (5.4), |
|
|
|
||||
|
Рис. 5.11 |
|
|
M x = Pкр y, |
EIy′′ + Pкр y = 0. |
|
|
|
|
|
|
|
|
и однородное дифференциальное уравнение изгиба получаем в виде: |
||||||
|
|
|
y′′ + n2 y = 0 , |
|
(5.9) |
|
где |
|
|
n = |
Pкр . |
|
(5.10) |
|
|
|
|
EI |
|
|
Решение уравнения (5.9) имеет вид:
y = A sin(nx)+ B cos(nx),
где A, B – постоянные интегрирования, определяемые по кинематическим граничным условиям: при x = 0, y = 0; при x = l , y = 0.
По первому условию B = 0 и изогнутая ось стержня является синусоидой, определяемой уравнением
y = A sin(nx). |
(5.11) |
По второму условию A sin(nl)= 0, и так как A ≠ 0 , то sin(nl)= 0 .
Наименьшее значение положительного корня (отличного от нуля) этого уравнения nl =π и по формуле (5.6)
P |
= |
π 2 EJ |
, |
(5.12) |
|
кр |
l |
2 |
|
|
|
|
|
|
|
||
т.е. получена известная формула Л. Эйлера.
Установим физический смысл постоянной A в формуле (5.11), так как она осталась неопределенной.
Подставив в уравнение (5.11) значение n = πl и x = 2l , имеем:
83
π |
|
l |
|
π |
|
|
||
y = A sin |
|
|
|
= A sin |
|
|
= A 1, |
|
2 |
2 |
|||||||
l |
|
|
|
|
|
|||
т.е. A = ymax = y0 – максимальное отклонение стержня от начального его по-
ложения в середине пролета стойки.
Изогнутую ось стержня в деформированном состоянии можно представить в виде:
y = y0 sin |
π x |
. |
(5.13) |
|
|||
|
l |
|
|
Полученное выше (по второму граничному условию) равенство sin(nl)= 0 удовлетворяется, если nl =π , nl = 2π , nl = 3π и т.д., что под-
тверждает зависимость формы деформации элемента (рис. 5.2) от значений критических сил.
Заметим, что приведенные выше решения статическим методом будут справедливы при малых перемещениях (потеря устойчивости в малом), так как использовалось приближенное дифференциальное уравнение изгиба (5.4), справедливое при малых деформациях.
Статический метод имеет разновидности в зависимости от способа нахождения уравнения устойчивости (5.3):
–метод непосредственного интегрирования дифференциального уравнения изогнутой оси стержня;
–использование метода сил и метода перемещений;
–интегрирование уравнений в конечных разностях;
–приближенные способы, основанные преимущественно на методе перемещений.
Энергетический метод. Этот метод используется в расчетной практике для приближенного определения критических нагрузок для стоек сложного и
втом числе переменного сечения, а так же для плоских и пространственных рам, ферм, комбинированных систем. В основу его положен энергетический признак равновесия, согласно которому полная потенциальная энергия системы П в состоянии устойчивого равновесия имеет минимальное значение, в
84

состоянии неустойчивого равновесия – максимальное, а в случае безразличного состояния системы приращение потенциальной энергии ∆П должно быть рано нулю. Этот принцип наглядно прослеживается на примере абсолютно твердого шарика, помещаемого на различных поверхностях (рис 5.12).
а) |
б) |
в) |
|
Q |
Q |
Q |
|
П=max |
|||
П=min |
∆П=0 |
Рис. 5.12
Шарик, находящийся на вогнутой сферической поверхности, располагается в самой низкой ее точке (рис. 5.12а) и при любом отклонении его от этого положения он под действием собственного веса Q , будет возвращаться в начальное положение. Располагаясь в самой низкой точке сферы, шарик обладает минимальной потенциальной энергией и находится в состоянии устойчивого равновесия. Находясь в верхней точке выпуклой сферической поверхности (рис. 5.12б), шарик находится в состоянии неустойчивого равновесия и обладает максимальной потенциальной энергией. При любом на него воздействии он будет перемещаться в более низкие точки сферы, занимая устойчивое положение. Если шарик находится на горизонтальной плоскости (рис. 5.12в), то при любых горизонтальных перемещениях его потенциальная энергия не изменяется. Приращение потенциальной энергии ∆П = 0 , что соответствует безразличному состоянию системы.
Полная потенциальная энергия упругой системы численно равна работе внешних и внутренних сил, совершаемой ими при переводе системы из деформированного состояния в начальное, недеформированное. Изменение потенциальной энергии определяется равенством:
∆П =U −T , (5.14)
где U , T – изменения работы соответственно внутренних и внешних сил сис-
темы при небольшом отклонении ее от состояния равновесия.
85

Расчет систем на устойчивость энергетическим методом состоит в следующем. При бесконечно малом отклонении системы от начальной формы равновесия в ее элементах возникнут дополнительные внутренние силы
M ,Q и N . Эти внутренние силы M ,Q и N и внешние нагрузки (q, P) со-
вершат некоторую работу. Если окажется, что U > T , (∆П > 0), то система устойчива, а если U < T , (∆П < 0) – система неустойчива. Равенство U = T
дает значения нагрузок, при которых становится возможной потеря устойчивости первоначальной формы равновесия системы.
В случае безразличного состояния системы будем иметь ∆П =U −T = 0 ,
откуда |
|
|
|
|
|
|
|
|
U =T . |
|
|
|
|
|
(5.15) |
|
Как известно, потенциальная энергия внутренних сил определяется вы- |
||||||||||||||||
ражением: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
l |
|
|
2dx |
m |
l |
µ |
|
2dx |
m |
l |
|
|
2dx |
|
|
|
|
|
|
|
||||||||||||
|
M |
Q |
N |
|
|
|||||||||||
U = ∑ |
∫ |
|
|
|
+ ∑ |
∫ |
|
|
|
+∑ |
∫ |
|
|
|
, |
(5.16) |
|
2EI |
2GF |
|
2EF |
||||||||||||
1 0 |
|
1 0 |
1 0 |
|
|
|
||||||||||
где M ,Q и N – дополнительные усилия в элементах системы, возникаю-
щие при отклонении ее от начального положения равновесия; m – количество элементов в системе;
µ – коэффициент, учитывающий неравномерность распределения ка-
сательных напряжений в сечениях элементов.
Для систем из элементов сплошного сечения, пренебрегая влиянием поперечных и продольных сил, имеем:
|
1 |
m |
l |
|
2dx |
|
|
|
M |
|
|||||
U = |
2 |
∑1 |
0∫ |
EI |
|
, |
|
или, учитывая зависимость − EIy′′ = M x : |
|
|
|
|
|||
|
1 m |
l |
|
′′ |
2 |
||
U = |
|
∑ |
|
|
|
||
|
|
|
|
||||
2 |
∫EI[y |
(x)] dx . |
|||||
|
1 |
0 |
|
|
|
|
|
(5.17)
(5.18)
Работу вертикально приложенных узловых нагрузок можно определить:
n
T = ∑Piδi , (15.19)
i =1
86
где δi |
– перемещение точки приложения внешней силы по ее направлению, |
||||||||||||||
вызванное изгибом сжимаемого стержня. |
|
|
|
|
|
||||||||||
а) |
P |
PКР |
|
б) |
|
|
|
|
|
Например, перемещение силы Р по ее |
|||||
|
δ |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
направлению при изгибе стержня, |
|||||||||
|
|
δ |
|
|
∆ |
|
|
|
|
||||||
|
dx |
|
dx |
dω |
|
|
|
|
|
изображенного на рис. 5.13а, примем |
|||||
|
|
|
|
|
|
|
|
равным δ . Для определения δ |
выде- |
||||||
|
|
|
|
|
ω |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx cosd |
|
|
|
|
лим из |
стержня бесконечно |
малый |
|||
|
|
|
|
|
|
|
|
|
элемент dx и определим вертикаль- |
||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Рис. 5.13 |
|
|
|
|
|
ное смещение его конца ∆δ |
|
||||||
при повороте элемента dx на некоторый малый угол dϕ (рис. 5.13б): |
|
||||||||||||||
|
|
∆δ |
= dx − dxcosϕ = (1 − cosϕ)dx = |
2sin2 dϕ dx . |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
Ввиду малости угла dϕ можно принять |
|
|
|
|
|||||||||||
|
|
|
sin2 |
dϕ |
dϕ |
2 |
= |
1 |
tg 2dϕ |
= |
1 |
(y′)2 . |
|
||
|
|
|
2 |
= |
|
|
4 |
4 |
|
||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
Тогда |
∆δ = 2 |
1 (y′)2 dx |
= 1 |
(y′)2 dx |
и полное перемещение при изгибе стержня: |
||||||||||
|
|
4 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ = 1 |
l |
(y′)2 dx . |
|
|
|
(5.20) |
|||
|
|
|
|
|
|
∫ |
|
|
|
||||||
|
|
|
|
|
|
|
2 |
0 |
|
|
|
|
|
|
|
Работа внешней силы для рассматриваемого стержня
T = Pкрδ = Pкр |
1 |
∫l (y′)2 dx . |
(5.21) |
|
2 |
||||
|
0 |
|
Приравнивая правые части равенств (5.18) и (5.21), из полученного уравнения имеем:
|
|
l |
′′ |
2 |
dx |
|
|
|
|
∫ |
|
||||
|
|
EI [y (x)] |
|
|
|||
P |
= |
0 |
|
|
|
. |
(5.22) |
|
|
|
|
||||
кр |
|
|
∫l [y′(x)]2 dx |
|
|||
|
|
|
|
||||
|
|
|
0 |
|
|
|
|
Формула (5.22) справедлива при любых закреплениях концов стержня. Для системы с несколькими сжатыми стержнями критические нагрузки
87

для них находятся приравниванием правых частей равенств (5.18) и (5.19). При этом внешние узловые нагрузки целесообразно выразить через одну из
них с поправочными множителями ki |
и формула (5.22) примет вид: |
|
||||||
|
|
m |
l |
′′ |
2 |
dx |
|
|
|
|
|
|
|
||||
|
|
∑∫EI [y (x)] |
|
|
||||
P |
= − |
1 0 |
|
|
|
, |
(5.23) |
|
|
|
|
|
|||||
кр |
|
n |
n l |
[y′(x)]2 dx |
|
|||
|
|
∑ki ∑∫ |
|
|||||
|
|
i=1 |
1 0 |
|
|
|
|
|
где n – число загруженных стержней системы. Критические нагрузки получаем по условию:
(Pкр )i = ki Pкр .
Применение энергетического метода рассмотрим на примере упругого шарнирно опертого стержня постоянного сечения (рис. 5.11), приняв уравнение упругой линии в деформированном его состоянии по формуле (5.13), т.е.
y = y0 sin πlx ,
где y0 – прогиб стержня в середине пролета.
|
|
|
|
|
|
|
π |
|
π x |
|
|
|
|
|
|
|
|
|
|
π 2 |
|
πx |
|
|
|
|||||||
В нашем случае |
y′ = y0 l |
|
cos |
|
|
|
и |
|
|
y′′ = −y0 |
|
sin |
|
l . |
|
|
||||||||||||||||
|
l |
|
|
|
|
l 2 |
|
|
|
|||||||||||||||||||||||
Числитель в выражении (5.22) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
l |
′′ |
2 |
|
|
2 π |
4 |
l |
π x |
|
|
|
2 π |
4 |
|
l |
|
|
|
|
2 π |
4 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
∫ |
|
|
|
|
|
|
|
∫sin |
|
|
dx = |
EI y0 |
|
|
|
|
|
|
|
= |
EI y0 |
|
|
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
EI [y |
(x)] dx = EI y0 |
l |
4 |
|
l |
|
l |
4 |
|
2 |
2l3 |
|||||||||||||||||||||
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Знаменатель в выражении (5.22) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
l |
|
|
|
|
|
|
2 |
l |
|
|
|
|
|
|
2 |
|
l |
|
|
|
|
|
π |
2 |
|
|
|
|
|||
|
∫ |
[y′(x)] |
2dx |
= y02 π |
|
|
∫cos2 π x dx =y02 π |
|
|
= y02 |
|
. |
|
|
|
|||||||||||||||||
|
|
|
|
|
2 |
|
2l |
|
|
|
||||||||||||||||||||||
|
0 |
|
|
|
|
|
l2 |
0 |
|
|
l |
|
|
|
l2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
Критическая нагрузка по формуле (5.22) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
P |
|
= EI y |
2 π 4 |
|
|
2l |
= |
π 2 EI . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
0 2l3 |
y02 π 2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
кр |
|
|
|
|
|
|
|
l 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Получено точное решение, так как изогнутая ось стойки принята по той кривой, которая соответствует действительному изгибу стойки в момент потери ею устойчивости (5.13).
88
Недостатком энергетического метода является то, что необходимо задаваться уравнениями упругих линий изогнутых стержней в момент потери устойчивости. Отсюда и приближенность получаемого решения этим методом. Чем ближе принятые уравнения изогнутых осей стержней к действительной их форме деформации в момент потери устойчивости, тем точнее получаемый результат. Кроме того, для вычисленной критической нагрузки неизвестна степень точности ее значения. В общем случае энергетический метод дает завышенные значения критических сил.
Динамический метод. В общем случае решение динамическим методом сводится к отыскиванию уравнений движения масс системы и определению частот собственных колебаний этих масс. Равновесие системы будет устойчивым, если колебания ее масс будут затухающими или просто восстанавливается первоначальное состояние системы. Значение критической нагрузки находят по частотам собственных колебаний. Если эта частота положительна, то равновесие устойчиво; если она равна нулю – система в критическом (безразличном) состоянии, а мнимое значение наименьшей частоты соответствует неустойчивому состоянию системы.
В расчетной практике решение задач устойчивости упругих стержневых систем выполняется, как правило, статическим или энергетическим методами, которыми мы воспользуемся в дальнейшем.
5.6.Устойчивость стержней постоянного сечения
сжесткими опорами
Формула Л.Эйлера для определения наименьшей критической сжимающей нагрузки, действующей на упругий стержень постоянного сечения с шарнирно опертыми концами, имеет вид (5.12):
P |
= |
π 2 EI |
. |
|
кр |
l |
2 |
|
|
|
|
|
||
Для стержней постоянного сечения с различными опорными закрепле-
89
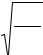
ниями критическая нагрузка может быть определена по общей формуле:
P |
= |
π 2 EI |
= |
π 2 EI |
, |
(5.24) |
кр |
|
l02 |
|
(µl)2 |
|
|
|
|
|
|
|
где l0 – приведенная (расчетная) длина сжатого стержня (это понятие впер-
вые введено Ф.С. Ясинским в конце XIX века и лежит в основе практических методов расчета сжатых и сжато-изогнутых элементов конструкций согласно действующих норм);
µ – коэффициент расчетной длины, определяемый |
|
|||
µ = |
l0 |
, |
(5.25) |
|
l |
||||
|
|
|
||
l – геометрическая длина сжатого стержня. |
|
|||
Из равенства (5.24) получаем формулу для определения расчетной дли- |
||||
ны сжатого стержня: |
|
|
||
l0 =π |
EI , |
(5.26) |
||
|
|
Pкр |
|
|
где Pкр – значение критической нагрузки для данного стержня.
В таблице 5.1 приведены формулы для определения критических сил для центрально нагруженных упругих стержней постоянного сечения с различными опорными закреплениями, расчетные длины этих стержней и значения коэффициента расчетной длины µ .
90
