
Строительная механика
.pdf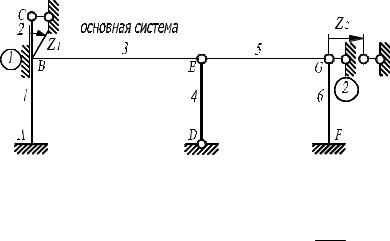
B, E, G . Направления смещений введенных связей при построении еди-
ничных эпюр указаны в основной системе стрелками. Там же цифрами 1, 2, …, 6 указаны порядковые номера стержней.
Рис. 4.12
Вычислим погонные жесткости (i) стержней: in = EIn , где EIn – жест- ln
кость n - го стержня, ln – его длина. Так как погонные жесткости всех стержней выражены через EI , то численное значение EI может быть принято любым (не равным нулю) числом, и соотношение жесткостей стержней в системе будет соблюдаться. Примем EI =8:
i |
= |
|
EI1 |
= |
EI = |
8 = 2; |
|
i |
= |
EI2 = |
EI = |
8 |
= 4; |
|||||||||
|
|
|
|
|
2 |
|||||||||||||||||
1 |
|
|
|
l1 |
l1 |
4 |
|
|
2 |
|
l2 |
|
|
l2 |
|
|
|
|||||
i |
= |
EI3 |
= 8EI = |
8 8 |
=8; |
i |
= EI4 = |
2EI = |
|
2 8 |
= 4; |
|||||||||||
|
|
|
|
|
4 |
|||||||||||||||||
3 |
|
|
|
l3 |
l3 |
8 |
|
4 |
|
l4 |
|
|
l4 |
|
|
|
|
|||||
i |
= |
|
|
EI5 |
= |
6 8 |
= 8; |
|
|
i |
= |
EI6 |
= |
EI |
= |
8 |
= 2. |
|||||
|
|
|
6 |
|
|
|
4 |
4 |
||||||||||||||
5 |
|
|
|
l5 |
|
|
|
|
6 |
|
l6 |
|
|
|
|
|
||||||
В нашем случае канонические уравнения имеют вид:
r |
Z |
+ r |
Z |
2 |
+ R |
= 0; |
||||
|
11 |
|
1 |
12 |
|
|
1p |
|
||
|
|
|
Z |
+ r |
|
Z |
|
+ R |
= 0. |
|
r |
|
|
2 |
|||||||
|
21 |
1 |
22 |
|
|
2 p |
|
|||
Для вычисления коэффициентов при неизвестных и свободных членов канонических уравнений построим в основной системе эпюры изгибающих моментов от поочередного смещения добавленных связей на единицу и действия заданной нагрузки.
Повернем дополнительно введенную (защемляющую) связь на угол
61
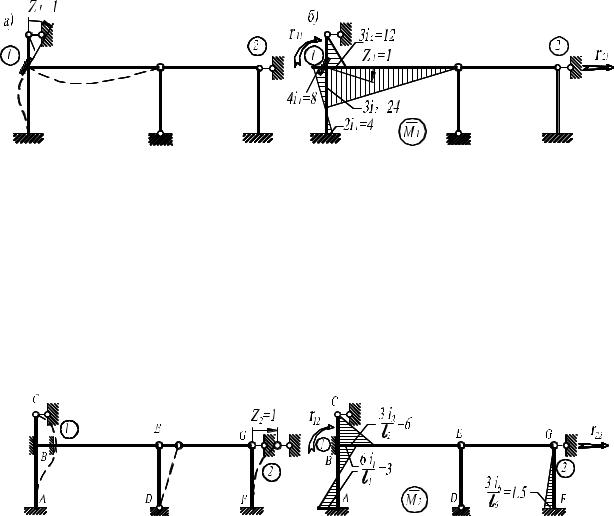
Z1 =1. На рис. 4.13а показаны изогнутые оси стержней от этого воздействия.
Изогнулись только те стержни, которые примыкают к узлу 1, а остальные стержни остались прямолинейными. Изгибающие моменты, возникающие при изгибе стержней, и эпюры изгибающих моментов на стержнях приведены на рис. 4.13б (см. табл. 4.1. готовых решений).
Рис. 4.13
Изогнутые оси стержней в основной системе при линейном перемещении связи 2 в горизонтальном направлении связи 2 показаны на рис. 4.14а. Изогнутся стержни AB, BC и FG . Стержень DE повернется, не изгибаясь,
стержни BE и EG – сместятся вправо, тоже не изгибаясь. Эпюры изгибающих моментов на стержнях от этого воздействия приведены на рис. 4.14б.
а) б)
Рис. 4.14
От действия заданной нагрузки изгибаться будут стержни BE и EG , к которым непосредственно приложена нагрузка. Остальные стержни не изгибаются и изгибающие моменты в них не возникают. Эпюры изгибающих моментов в стержнях от этого воздействия приведены на рис. 4.15.
62
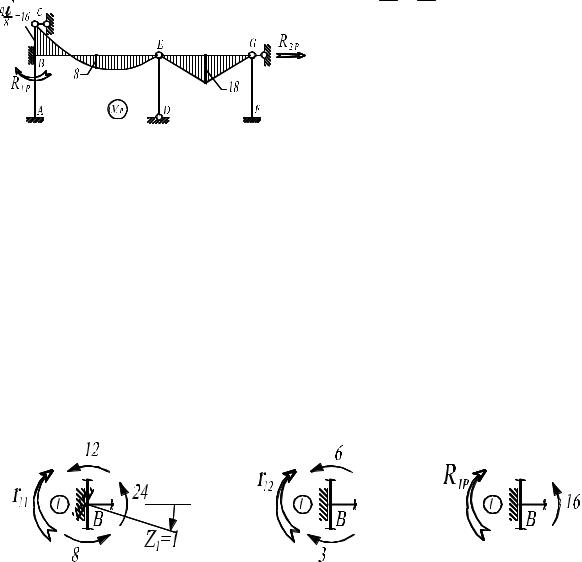
|
На эпюрах от единичных смеще- |
||
|
ний (M 1 , M 2 ) |
и от действия за- |
|
|
данной нагрузки (M p ) |
стрелками |
|
|
указаны положительные направ- |
||
|
ления реакций, совпадающие с |
||
|
направлением |
соответствующих |
|
Рис. 4.15 |
перемещений. |
|
|
Вычислим реактивные моменты в дополнительно введенной защем- |
|||
ляющей первой связи, рассматривая равновесие узла. На рис. 4.16а обозначе- |
|||
ны значения моментов в отсекаемых стержнях при повороте этой связи на |
|||
угол Z1 =1 и показано вычисление реактивного момента r11. На рис. 4.16б, |
|||
приведено вычисление реактивного момента r12 , а на рис. 4.16в – вычисление |
|||
реактивного момента R1p от заданной нагрузки. |
|
|
|
a) |
б) |
в) |
|
∑M1 = 0; |
∑M1 = 0; |
∑M1 = 0; |
|
r11 −12 − 24 −8 = 0, |
r12 +3 −6 = 0, |
R1 p +16 = 0, |
|
→ r11 = 44. |
→ r12 = 3. |
→ R |
= −16. |
|
|
1 p |
|
|
Рис. 4.16 |
|
|
Реакцию в дополнительно введенной связи, препятствующей линейно- |
|||
му смещению узлов рамы |
в горизонтальном направлении, определим, рас- |
||
сматривая равновесие отсеченной части рамы (рис. 4.17). |
|
|
|
63
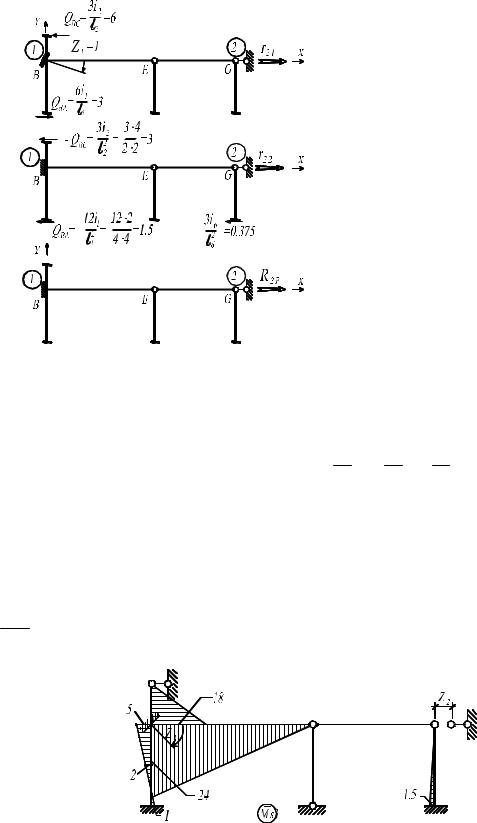
a) |
|
∑X = 0 ; r21 +3 −6 = 0, |
|
→ r21 =3.
б) |
∑ X = 0 ; |
r22 −3 −1,5 − |
|
−0,375 = 0,
→ r22 = 4,875.
в)
∑X = 0 ; R2 р = 0,
Рис. 4.17
Проверим достоверность вычисленных значений коэффициентов при неизвестных и свободных членов канонических уравнений. Для этого строим суммарную единичную эпюру по условию M S = M 1 + M 2 (рис. 4.18) и про-
верим соблюдение условия (4.5):
|
l |
|
2s dx |
|
1 1 |
|
|
2 |
|
4 |
|
|
|
|
∑ |
M |
|
|
|
|
(5 |
|
|
+1 1)+ |
|||||
0∫ |
EI |
= |
8 218 |
2 |
|
|
18 + |
|
5 |
+ 4 2 2 |
||||
3 |
6 8 |
|||||||||||||
+ 818 12 24 8 23 24 + 18 121,5 4 231,5 = 27 + 3,5 + 24 + 0,375 =54,875.
Рис. 4.18
Алгебраическая сумма коэффициентов при неизвестных
∑ri k = r11 + r12 + r21 + r22 = 44 +3 +3 + 4,875 = 54,875 .
64
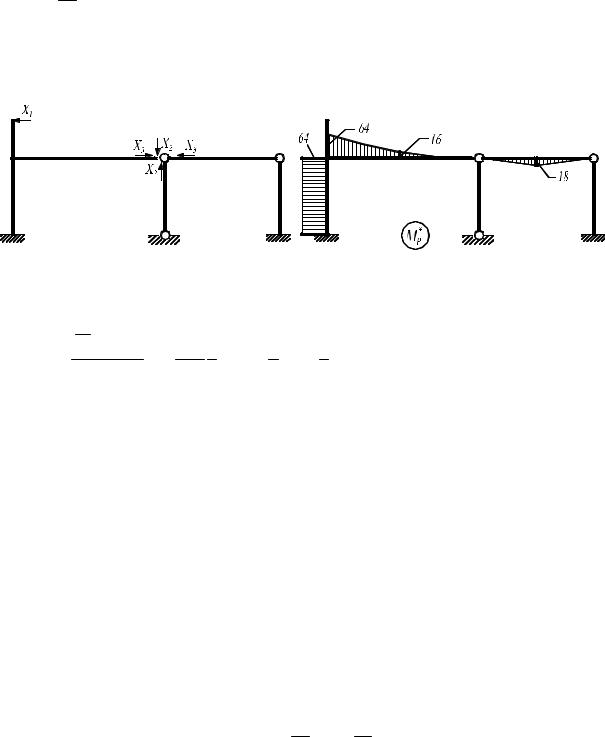
Следовательно, реакции ri k найдены верно.
Для проверки свободных членов уравнений суммарную единичную эпюру (M S )умножаем на грузовую эпюру (M P ), построенную в О.С. метода сил. На рис. 4.19а показана основная система метода сил, а на рис. 4.19б – эпюра изгибающих моментов в этой системе от заданных нагрузок.
а) |
б) |
основная система |
|
м.с. |
|
Рис. 4.19
∑∫ M s MEI*pdx = −818 13 64 8 34 24 + 18 64 4 2 = −48 + 64 =16
∑Ri p = R1p + R2 p = −16 + 0 = −16,
|
|
s M |
*p dx |
|
|
т.е. ∑∫ |
M |
= −∑Ri p , |
что подтверждает правильность полученных зна- |
||
|
EI |
|
|||
|
|
|
|
|
чений Ri p .
Система канонических уравнений принимает вид:
44Z1 + 3Z2 −16 = 0; откуда |
Z1 |
= 0,379562; |
3Z1 + 4,875Z2 + 0 = 0, |
Z2 |
= −0,233577. |
Проверка правильности решения системы уравнений остается обычной (приведена в методе сил п. 3.4).
Окончательную эпюру изгибающих моментов получаем по условию
M = M p + M 1Z1 + M 2Z2 .
Эпюры изгибающих моментов от фактических значений перемещений и результирующая эпюра моментов приведены на рис. 4.20а,б,в.
65
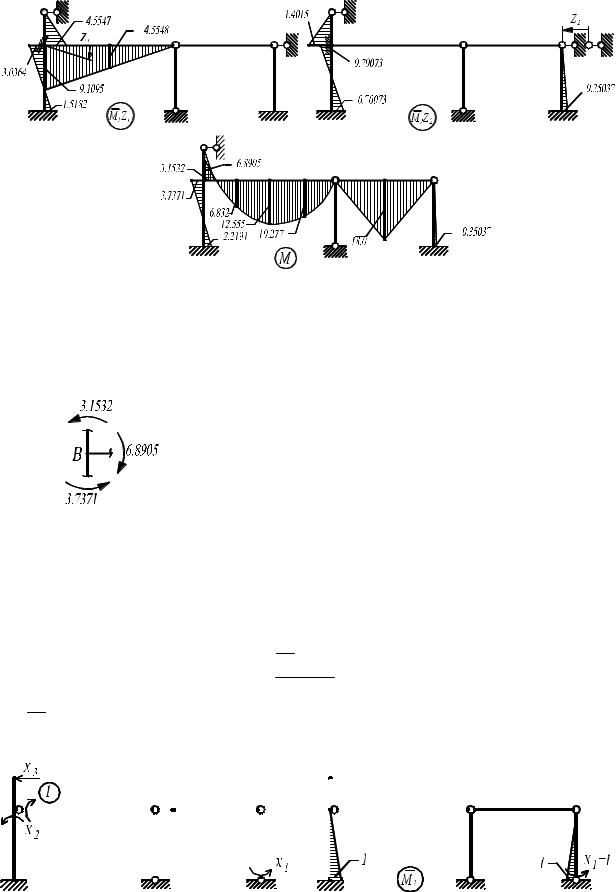
a) |
б) |
в)
Рис. 4.20
Выполним проверки правильности окончательной эпюры изгибающих моментов (см. п.4.5).
|
В статической проверке проверяют равнове- |
||
|
сие узлов ( ∑M узл. = 0 ). |
||
|
В нашем случае проверяем равновесие |
||
|
узла B. (Рис. 4.21). |
||
Рис. 4.21 |
∑M B = |
6,8905 − 3,1532 − 3,7371 = |
|
= 6,8905 |
− 6,8903 = 0,0002 ≈ 0. |
||
|
|||
В кинематической проверке находят перемещение в заданной системе по направлению любого неизвестного Хi по формуле:
∑∫M EIi Mdx = 0,
где M i – любая единичная эпюра в любой О.С. метода сил.
a) |
|
|
|
|
|
б) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.22
Примем основную систему метода сил, как показано на рис. 4.22а.
66
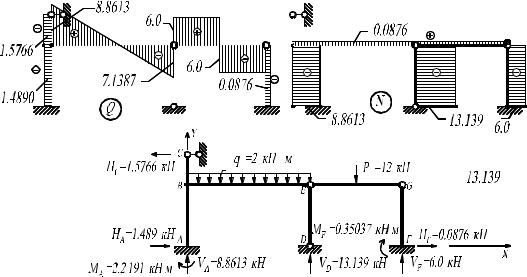
Единичная эпюра |
M |
1 приведена на рис. 4.22б. Тогда |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
Mdx |
|
1 1 |
|
|
2 |
|
1 |
|
|
1 |
|
1 |
|
|
|
2 |
|
|
|||
∑ |
|
M |
1 |
|
|
|
|
− |
|
1 |
4 |
|
0,35037 |
= |
|||||||||||||
∫ |
|
|
|
= |
|
|
|
1 4 |
|
2,2189 − |
|
3,7371 |
|
|
|
||||||||||||
|
|
|
|
8 2 |
|
3 |
8 |
2 |
3 |
||||||||||||||||||
|
|
|
|
EI |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||||||
= 0,0583920 − 0,058395; |
µ = 0,005%. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Эпюра поперечных (Q) и продольных(N ) сил, а также схема рамы с указанными значениями внешних нагрузок и реакций опор приведены на рис. 4.23а,б,в.
a) |
|
|
|
|
|
б) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в)
Рис. 4.23
Построение этих эпюр и проверки их правильности выполняются теми же способами, что и в методе сил.
Выполним проверки равновесия системы в целом, пользуясь уравне-
ниями (3.7).
∑X = 0; −1,5766 +1,489 + 0,0876 = −1,5766 +1,5766 = 0;
∑Y = 0; 8,8613 +13,139 + 6,0 −12,0 − 2,0 8,0 = 28,0 − 28,0 = 0.
∑MG = 0; 2,2191 + 8,8613 14 −1,489 4 −1,5766 2 −
− 2 8 10 +13,139 6 −12 3 + 0,35037 − 0,0876 4 =
= 205,46 − 205,46 = 0
Полученные результаты свидетельствуют о правильности построения эпюр и о правильности решения задачи.
67
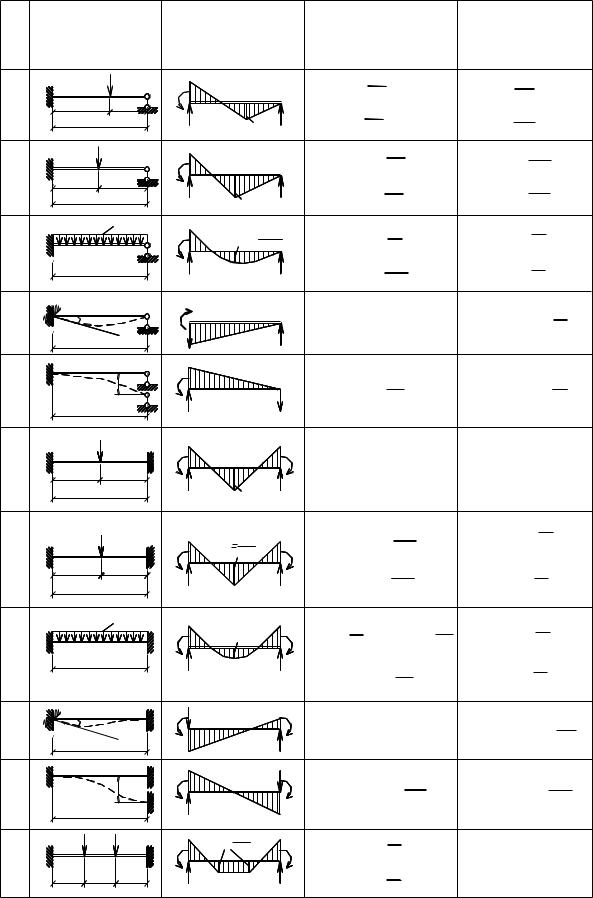
Таблица реактивных моментов и сил в однопролетных балках |
Таблица 4.1 |
№№
п/п Схемы
P
А
1 ul С vl l
P
А
2 |
|
l/2 С |
l/2 |
|
|
l |
|
|
А |
|
q |
3 |
l |
|
|
|
|
|
|
4 |
А |
z |
|
|
|
l |
|
5 |
А |
|
|
|
δ=1 |
|
|
|
l |
|
|
|
|
|
|
|
|
P |
|
6 |
А |
ul С |
vl |
|
|
l |
|
|
А |
P |
|
7 |
l/2 С |
l/2 |
|
|
|
l |
|
|
А |
|
q |
8 |
l |
|
|
|
|
|
|
9 |
А |
z |
|
|
|
l |
|
А
10 δ=1
l
11 А 
P P
l/3 l/3 l/3
Эпюры изгиба- |
Реактивные |
|
ющих моментов |
||
моменты |
||
и реакции |
||
|
|
MA |
|
|
|
MA = |
Pl |
|
|
|
|
|
|
2 |
|
||||||
В |
|
|
|
3 |
|
v(1-v ) |
||||||||||||||
|
RA |
MC |
RB |
MC = |
|
Pl |
|
|
2 |
|
|
|
|
|
||||||
|
|
2 |
|
u v(3-u ) |
||||||||||||||||
|
M |
|
|
|
|
MA= |
- |
|
3 |
|
|
|
|
|
||||||
В |
A |
|
|
|
|
|
16Pl |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
R |
MC |
RB |
|
M |
|
= |
|
5 Pl |
|
|
|||||||||
|
A |
|
|
|
|
|
C |
|
32 |
|
|
|
|
|||||||
В |
MA |
MC= |
ql2 |
|
|
MA = - |
|
|
ql2 |
|
|
|||||||||
|
|
16 |
|
|
89 ql2 |
|
||||||||||||||
|
R |
|
|
RB |
|
M |
|
|
= |
|
||||||||||
|
A |
|
|
|
|
|
|
|
max |
128 |
|
|
|
|||||||
|
MA |
|
|
|
|
|
|
|
|
|
|
|||||||||
В |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
RB |
|
MA= +3iz |
|
|
||||||||||||
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
MA |
|
|
|
|
M = - |
3i |
|
|
|
|
|
||||||||
|
|
|
|
RB |
|
|
δ |
|
|
|||||||||||
|
R |
|
|
|
|
|
|
A |
|
|
l |
|
|
|
|
|
|
|||
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В MA |
|
|
MB |
|
MA= -uv2 Pl |
|
|
|||||||||||||
|
|
|
|
|
M B=+u 2vPl |
|
|
|||||||||||||
|
R |
|
|
RB |
|
|
|
|||||||||||||
|
M |
|
|
MC=2u |
2 |
v |
2 |
Pl |
|
|||||||||||
|
A |
|
|
|
|
|
|
|
||||||||||||
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В MA MC |
Pl |
|
MB |
|
M |
|
= - |
|
Pl |
|
|
|||||||||
|
|
8 |
|
|
|
|
|
|
A |
|
|
|
|
8 |
|
|
|
|||
|
R |
|
|
RB |
|
MB =+ |
|
Pl |
|
|
||||||||||
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
||
В MA |
|
|
MB |
M |
=- |
ql2 |
|
M |
|
|
=+ |
ql2 |
||||||||
|
|
|
|
|
12 |
|
B |
12 |
||||||||||||
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|||||||
|
R |
|
|
RB |
|
|
M =+ |
ql2 |
|
|
||||||||||
|
A |
|
|
|
|
|
24 |
|
|
|||||||||||
В MA R |
|
|
MB |
|
|
|
|
C |
|
|
|
|
|
|||||||
|
|
|
M = +4iz |
|
|
|||||||||||||||
|
A |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
В MA |
|
|
RB |
|
MB |
= +2 i z |
|
|
||||||||||||
|
RB |
MB |
M |
=M |
= - |
|
|
6i |
δ |
|||||||||||
|
|
|
|
|
|
|
l |
|||||||||||||
|
RA |
|
|
|
|
A |
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 Pl |
|
|
|||||
В MA M= P9l |
|
MB |
|
M |
=- |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
A |
|
|
|
9 |
|
|
|
|
|
||
|
R |
|
|
R |
|
M |
B |
=+ |
2 Pl |
|
|
|||||||||
|
|
|
B |
|
|
|
|
|
|
|
9 |
|
|
|
|
|
||||
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Опорные
реакции
RA= Pv2 (3-u2)
RB= Pu2 (32 -u )
R = |
|
11 |
P |
||||
16 |
|
||||||
A |
|
|
|||||
R = |
|
|
5 |
P |
|||
|
16 |
||||||
B |
|
|
|||||
RA= |
5 |
|
ql |
||||
|
8 |
||||||
RB= |
3 |
|
ql |
||||
|
8 |
|
|||||
RA=RB= l3iz
RA=RB= 3il2 δ
RA =v 2(1+2u)P RB = u2(1+2v)P
R A= P2
R B= P2
R A= ql2
R B= ql2
R |
=R = |
6i |
A |
B |
l |
R =R = |
12i2 δ |
|
A |
B |
l |
|
|
|
RA= P
RB= P
68
Глава 5
Основы устойчивости стержневых систем
5.1.К истории вопроса
Впервой и второй частях курса строительной механики изучаются методы определения усилий и перемещений в статически определимых и неопределимых стержневых системах. Практика эксплуатации сооружений, имеющих в своей структуре сжатые элементы определенной гибкости, показала, что во многих случаях расчетов на прочность недостаточно для полной оценки надежности сооружения. Если расчетом на прочность установлено, что напряжения в сечениях элементов не превышают допускаемых нормами расчетных сопротивлений материала, то это еще не значит, что конструкция
впериод эксплуатации будет находиться в безопасном состоянии. Крушения крупных инженерных сооружений (например, мостов) часто происходили при напряжениях в сечениях элементов меньше допускаемых. Аварии сооружений во многих случаях происходили вследствие потери устойчивости сжатых элементов системы или же потери устойчивости сооружением своего положения.
В1744 году Л. Эйлер впервые получил формулу критической нагрузки для центрально сжатого гибкого стержня. Почти 100 лет формула Л. Эйлера не находила практического применения, так как в эксплуатируемых сооружениях того времени вопросы устойчивости не были определяющими. В то время не строились большепролетные конструкции, высотные сооружения и принятых из расчета на прочность сечений в массивных каменных и деревянных конструкциях было достаточно для обеспечения устойчивости их элементов.
Интенсивное строительство железных дорог со второй половины IX столетия потребовало возведения железнодорожных мостов, путепроводов с использованием стальных конструкций с более гибкими элементами, чем в применявшихся до этого времени конструкциях. В процессе возведения и в
69
период эксплуатации произошли крушения значительного числа железнодорожных металлических мостов с основными несущими стальными конструкциями. Одной из основных причин этих разрушений было несовершенство расчетов. В конструкциях были заложены предпосылки потери устойчивости сжатых стальных элементов.
Практика эксплуатации строительных конструкций, включающих гибкие сжатые элементы, показала, что без расчетов на устойчивость нельзя гарантировать безопасное состояние этих конструкций. Была востребована и получила дальнейшее развитие теория Л. Эйлера. Выделилась в самостоятельную науку и начала интенсивно развиваться теория расчета сооружений на устойчивость.
5.2. Формы потери устойчивости. Критическая нагрузка
Системы под действием нагрузок должны находиться в состоянии устойчивого равновесия. Каждому виду загружения сооружения нагрузками соответствует своя особая форма деформаций его элементов, соответствующие этим нагрузкам форма равновесия и положение системы.
Устойчивостью называют способность сооружения сохранять в деформированном состоянии соответствующие заданной нагрузке первоначальное положение и первоначальную форму равновесия при любых малых внешних или внутренних дополнительных возмущениях. Это означает, что если ка- ким-то малым возмущением на систему будет нарушено ее равновесное состояние, то после удаления причины возмущения система должна вернуться в первоначальное положение, т.е. сохранить свою первоначальную форму равновесия. В период возведения и эксплуатации сооружений возмущающие воздействия всегда имеют место. Это непредвиденные толчки сооружения (внешние возмущения), дефекты при изготовлении конструкции (внутренние возмущения).
Понятие «устойчивость» охватывает две разновидности этого явления: потерю устойчивости сооружением своего положения и потерю устойчиво-
70
