
Строительная механика
.pdf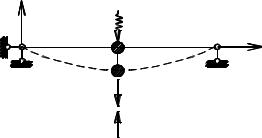
тенциальная энергия (энергия изгиба) достигает своего максимального значения и с ускорением возвращает массу к линии равновесия. К моменту расположения массы на линии равновесия потенциальная энергия убывает до нуля, но в это время скорость движения массы и ее кинетическая энергия достигает максимума и масса продолжает движение от линии равновесия, достигая максимального отклонения в обратном направлении и т.д. Таким образом, при колебаниях системы происходит переход одного вида энергии в другой.
Отметим, что приведенные выше зависимости и выводы будут справедливы для любых стержневых систем с одной степенью свободы при линейных колебаниях массы.
6.3.Вынужденные колебания систем с одной степенью свободы без учета сил сопротивления. Явление резонанса
Этот вид колебаний рассмотрим также на примере балки, изображенной на рис. 6.7. Примем динамическую нагрузку в виде гармонической, изме-
|
|
|
няющейся |
по |
синусоидальному |
y |
P sinθt |
x |
закону, т.е. |
P(t)= Psinθ t , где P и |
|
|
m |
||||
|
y |
|
θ – соответственно максимальная |
||
|
m |
|
составляющая |
(амплитуда) на- |
|
|
Im |
|
|||
|
|
|
|
|
|
|
S |
|
грузки и круговая частота возму- |
||
|
|
|
щающей силы. Приняв, что на- |
||
|
Рис. 6.7 |
|
правление перемещения массы m |
||
совпадает с направлением действия силы P(t), составим уравнение динами-
ческого равновесия
∑Y = 0; |
− P(t)− Im + S = 0 |
или, сохраняя предыдущие обозна- |
чения, |
my′′ + Cy = Psinθ t . |
|
141

Разделив на m слагаемые последнего равенства и обозначив
получаем неоднородное дифференциальное уравнение в виде y′′ +ω2 y = mP sinθ t .
Решение уравнения (6.13) в установившемся режиме имеет вид:
ω =  Cm ,
Cm ,
(6.13)
P |
|
y = Asin(ωt +ϕ)+ m(ω2 −θ 2 )sinθ t , |
(6.14) |
Из равенства (6.14) следует, что вынужденные колебания совершаются с той же частотой, которую имеет возмущающая сила, а амплитуда вынужденных колебаний (yдин ) зависит от величины составляющей P возмущаю-
щей силы P(t) и соотношения частот свободных и вынужденных колебаний.
Динамический прогиб можно представить в виде:
yдин = |
P |
P |
|
|
|
|
= |
|
|
P |
|
|
|
|
|
= |
|
P |
|
|
1 |
|
|
= yст |
|
1 |
|
|
, |
|||
m(ω2 −θ 2 )= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
θ 2 |
|
|
C |
|
θ 2 |
|
|
C |
|
|
θ 2 |
|
|
|
θ 2 |
|
|||||||||||||
|
|
mω2 1 |
− |
|
|
|
|
m |
|
1 − |
|
|
|
|
|
|
|
1 |
− |
|
|
|
|
1 |
− |
|
|
|
||||
|
|
|
|
2 |
|
|
|
2 |
|
|
|
2 |
|
2 |
||||||||||||||||||
|
|
|
|
ω |
|
|
|
|
ω |
|
|
|
|
|
|
ω |
|
|
|
|
ω |
|
||||||||||
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
или |
|
|
|
|
|
|
|
|
yдин = ycm µ , |
|
|
|
|
|
|
|
|
|
|
(6.15) |
||||||||||||
где |
|
|
|
|
|
|
|
|
µ = |
|
|
1 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
(6.16) |
|||||
|
|
|
|
|
|
|
|
|
|
|
θ 2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
ω2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
В выражении (6.15) |
ycm – статический прогиб, т.е прогиб, вызываемый |
|||||||||||||||||||||||||||||||
статическим действием амплитудного значения динамической нагрузки P(t).
Отвлеченная величина µ (6.16) носит название динамического коэф-
фициента и в системах с одной степенью свободы выражает отношение динамических величины (усилий, прогибов) к их статическим величинам. График изменения численных значений динамического коэффициента представлен на рис. 6.8. Если θ >ω , то динамический коэффициент µ имеет отрица-
тельные значения и правая кривая располагается ниже оси ωθ (на рис. 6.8 по-
казана пунктирной линией). Обычно значения коэффициента µ принимают-
142
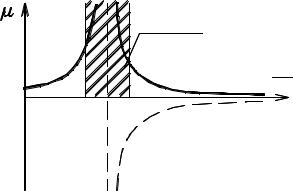
ся по абсолютной величине и обе кривые на графике располагаются выше оси ωθ (рис. 6.8).
зона
резонанса
1 |
|
|
|
0 |
0.75 |
1 |
1.25 |
|
θ
ω
Рис. 6.8
Из формулы (6.16) видно, что с приближением частоты возмущающей силы θ к частоте свободных колебаний ω динамический коэффициент, равно как и динамический прогиб (6.15), стремительно возрастают. При равенстве частот (θ =ω) динамический коэффициент становится равным беско-
нечности. Этот случай в технике носит название явления резонанса и представляет большую опасность для сооружения, так как усилия, перемещения и напряжения в элементах системы достигают больших значений. Для ответственных сооружений недопустимы не только явления резонанса, но и условия, при которых эти сооружения находились бы в зоне резонанса (рис. 6.8). Во избежание резонанса обычно обеспечивается условие, чтобы частота свободных колебаний системы отличалась от частоты вынужденных ее колебаний на 25-30%.
6.4. Свободные колебания систем с одной степенью свободы при учете сил сопротивления
Из графика, приведенного на рис. 6.6 следует, что масса, выведенная динамическим воздействием из состояния равновесия, будет совершать колебания с постоянной амплитудой неограниченное время. В реальных условиях процесс колебаний протекает иначе, так как неизбежны силы сопротивления,
143
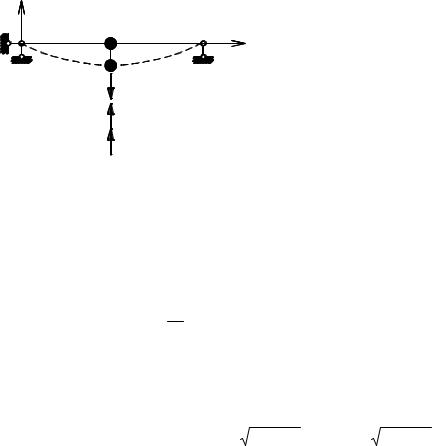
препятствующие колебаниям массы. Это сопротивление окружающей среды (например, воздуха), трение в опорных устройствах системы, внутреннее трение частиц материала в процессе деформирования системы и др. При наличии сил сопротивления часть энергии системы расходуется (необратимо) на преодоление этих сил и свободные колебания затухают. Влияние сил сопротивления на колеблющуюся систему учитывается обычно в предположении, что эти силы пропорциональны скорости колебания системы.
Затухающие колебания с принятыми начальными условиями проследим на примере упругой невесомой балки с сосредоточенной массой m (рис. 6.9).
y |
|
|
На выведенную из состояния |
||
о |
m |
x |
равновесия массу m действуют сила |
||
|
y |
|
инерции |
I m = −my′′, |
сила упругости |
|
m |
|
|
|
|
|
Im |
|
S = Cy |
и сила |
сопротивления |
|
S |
|
|
|
|
|
R |
|
R = β y′. |
|
|
|
Рис. 6.9 |
|
|
|
|
|
Уравнение динамического равновесия имеет вид: |
|
|||
|
∑Y = 0; |
S + R − Im = 0 , или my′′ + β y′ + C y = 0 . |
|||
Разделив слагаемые последнего равенства на m , учитывая соотноше-
ние (6.2) и обозначив mβ = 2k , получаем:
|
y′′+ 2k y′+ω2 y = 0 |
(6.17) |
Решение уравнения (6.17) имеет вид: |
|
|
y = e−k t (C1 sin( |
ω2 − k 2 t)+C2 cos( ω2 − k 2 t)), |
(6.18) |
где C1 и –C2 постоянные интегрирования, которые могут быть найдены из |
||
начальных условий: |
|
|
при t = 0 y = y0 ; |
υ = υ0 , |
|
где y0 и υ0 –соответственно начальные отклонение массы от положения равновесия и ее скорость.
По первому условию y = C2 1 = y0 и C2 = y0 .
144

По второму условию
y′ = e−k t (C1 cos( ω2 − k 2 |
t) ω2 − k 2 |
−C2 sin( ω2 |
− k 2 t) |
ω2 − k 2 )− |
||||||||
− k e−k t (C1 sin( |
ω2 − k 2 t)+C2 cos( |
ω2 − k 2 t)) |
|
|
|
|
||||||
Если t = 0, |
υ = (C1 |
ω2 − k 2 )− k y 0=υ0, C1 = |
υ0 + k y0 |
и |
уравнение |
|||||||
|
|
|
|
|
|
|
|
|
ω2 − k 2 |
|
|
|
колебаний (6.18) принимает вид: |
|
|
|
|
|
|
||||||
|
−k t |
υ 0+ k y0 |
|
2 |
2 |
2 |
2 |
|
|
|||
y = e |
|
|
2 |
|
2 |
sin( ω − k t)+ y0 cos( |
ω − k |
|
|
(6.19) |
||
|
ω |
− k |
|
t) . |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
Если y0 = 0 (при t = 0 масса находилась на линии статического равновесия),
то
y = e−k t |
υ0 |
sin( ω2 − k 2 t) |
(6.20) |
|
ω2 − k 2 |
|
|
Решение уравнения (6.20) справедливо при условии ω2 > k 2 .
При sin( ω2 −k 2 t)=1 максимальные значения прогиба:
ω2 −k 2 t)=1 максимальные значения прогиба:
ymax = e |
−k t |
υ0 |
. |
(6.21) |
|
ω2 −k 2 |
|||
|
|
|
|
Функция (6.20) имеет нулевые ординаты на оси t , если:
t = 0; t = |
π |
; t = |
2π |
и т.д. |
|
ω2 − k 2 |
|
ω2 − k 2 |
|
Из уравнение (6.20) следует, что с течением времени амплитуда колебаний уменьшается до нуля и колебания затухают. График таких свободных колебаний показан на рис. 6.10. В этом случае период и круговая частота свободных колебаний определяются зависимостями:
T = |
2π |
(6.22) |
c |
ω2 −k 2 |
|
|
|
|
ωc = |
ω2 − k 2 |
(6.23) |
145

y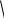
o
yn |
yn+1 |
t |
2-k2 |
||
2-k2 |
|
|
tTnc |
Tc |
|
tn+1 |
|
|
Рис. 6.10
Таким образом, при наличии сил сопротивления свободные колебания системы являются затухающими. Амплитуда колебаний в этом случае уменьшается до нуля. Если силы сопротивления и масса постоянны, то круговая частота и период колебаний так же остаются постоянными, зависящими от упругих свойств системы.
Для большинства инженерных сооружений коэффициент k мал в сравнении с частотой свободных колебаний ω. Поэтому в практических расчетах обычно пренебрегают силами сопротивления и определяют приближенные значения периода и частоты свободных колебаний по формулам (6.7) и (6.8),
вместо (6.22) и (6.23).
В качестве меры затухания колебаний часто используют так называемый логарифмический декремент колебаний. Он определяется так. В моменты времени tn и tn+1 (см. рис. 6.10) амплитуды колебаний по формуле (6.21)
будут:
|
|
|
yn |
= e |
−kt |
|
|
|
υ0 |
; |
yn+1 |
= e |
−k (t +T ) |
|
υ 0 |
. |
|||||||||
|
|
|
|
|
n |
|
|
|
n |
c |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
ω2 −k 2 |
|
|
|
|
|
|
|
ω2 − k 2 |
|
||||
Отношения этих амплитуд |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
y |
n |
= e |
k (t |
|
+T |
|
|
−t |
|
) |
= e |
kT |
|
|
|
|
|
|
yn |
|
|
= kT |
= const . |
|
|
|
|
n |
|
c |
|
n |
|
c |
; |
|
|
|
|
ln |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
yn+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yn+1 |
c |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
γ |
|
y |
n |
|
= kT |
|
|
|
|
|
|
|
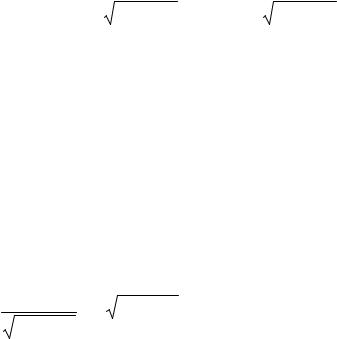
Обозначим |
|
|
|
|
|
|
|
|
= ln |
|
|
. |
|
|
|
(6.24) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yn+1 |
|
c |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
146
Безразмерная постоянная величина γ носит название логарифмиче-
ского декремента колебаний. Она также является динамической характеристикой системы и принимается по таблицам, имеющимся в справочной литературе.
6.5. Вынужденные колебания систем с одной степенью свободы при учете сил сопротивления
Для получения дифференциального уравнения этого вида колебаний воспользуемся рисунком (6.9), на котором сохранятся все силы, действующие на массу, и добавится возмущающая нагрузка, которую примем гармонической P(t)= P sinθ t , совпадающей по направлению (вниз) с перемещени-
ем массы. Тогда уравнение динамического равновесия будет:
∑Y = S + R − Im − P sinθ t = 0, или my′′+ β y′+C y = Psinθ t
Сохранив принятые выше обозначения, имеем
|
|
|
|
|
|
|
|
|
|
|
|
|
′′ |
|
′ |
2 P |
|
|
|
(6.25) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
y |
+ 2ky |
+ω y = m sinθ t |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Решение уравнения (6.25) включает общее (6.18) и частное решение и |
||||||||||||||||||||||
имеет вид: |
|
|
|
|
|
|
ω2 − k 2 t)+ C2 cos( ω2 − k 2 t))− |
|
||||||||||||||
y = e−kt (C1 sin( |
|
|||||||||||||||||||||
− |
|
|
|
|
|
P |
|
|
|
|
(2θk cosθ t − (ω |
2 |
−θ |
2 |
)sinθ t), |
(6.26) |
||||||
|
|
(ω |
2 |
−θ |
2 |
2 |
+ 4θ |
2 |
k |
2 |
|
|
|
|||||||||
|
m |
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где первое слагаемое выражает свободные колебания системы при наличии сил сопротивления, а второе – вынужденные колебания, причем первый сомножитель второго слагаемого – амплитуда колебаний (yдин ).
После преобразований, как показано выше, уравнение (6.26) принимает
вид:
|
−kt |
|
|
υ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
2 |
|
2 |
|
2 |
|
2 |
|
|
y = e |
|
|
|
2 sin( |
ω |
−k |
t) − yдин[2θk cosθ t −(ω |
−θ |
)sinθ t] (6.27) |
||||||
|
ω |
2 |
−k |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Свободные колебания с течением времени затухают, и колебания сис-
147
темы принимают установившийся характер вынужденных колебаний, определяемых вторым слагаемым уравнения (6.27). После преобразований второе слагаемое уравнения (6.27) принимает вид:
y = yдин sin(θ t + ε),
где |
|
|
|
|
|
|
yдин |
= m |
|
|
|
P |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
(6.28) |
||||
|
|
|
|
|
|
(ω2 −θ 2 )2 |
+ 4θ 2k 2 |
|
|
|
|
|
|
|
|||||||||||||||||
Учитывая принятые ранее обозначения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
ω2 = |
C |
|
; |
γ = kT; |
2k = |
2γ = |
γω |
, амплитуду вынужденных колебаний |
|||||||||||||||||||||||
|
m |
|
|
|
|
|
|
|
|
T |
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
можно представить в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
yдин |
= m |
|
|
P |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
= |
||||
|
(ω2 |
−θ |
2 )2 |
+ 4θ 2k 2 |
|
|
|
|
|
|
|
θ 2 |
2 |
|
θ 2 |
k |
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mω2 |
1 |
− |
|
|
|
+ |
4 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
4 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|
|
ω |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
= |
|
P |
|
|
|
1 |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
θ |
2 2 |
|
θ 2 |
γ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
− |
|
|
+ |
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
ω |
2 |
ω |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
или |
|
|
yдин = ycm µ; |
|
|
µ = |
|
|
|
|
|
1 |
|
|
|
|
|
|
, |
|
|
|
|
|
(6.29) |
||||||
|
|
|
|
|
|
|
θ 2 |
2 |
|
θ 2 |
γ 2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
+ |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|
|
ω |
π |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где µ – динамический коэффициент, зависимость которого от параметра γ можно представить в виде графика, который имеется в учебной и справочной литературе.
Из выражения (6.29) видно, что при совпадении частот θ и ω (случай резонанса) динамический коэффициент µ не обращается в бесконечность
(как это происходит без учета сил сопротивления), а имеет значение
µ = |
π |
(γ ≠ 0). Для реальных конструкций абсолютная величина декремента |
|
γ |
|
γзначительно меньше единицы. Например, для металлических конструкций
γ= 0,02 − 0,15, для деревянных – γ = 0,15 − 0,17 т. д. Поэтому в случае резо-
148
нанса (ω =θ) динамический коэффициент и амплитуда колебаний достигают недопустимо больших значений, и сооружению грозит разрушение, т.е. и в этом случаи резонанс остается большой опасностью для сооружения.
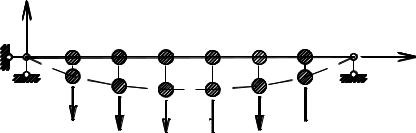
6.6. Свободные колебания систем со многими степенями свободы
Рассмотрим эти колебания на примере упругой невесомой балки с n сосредоточенными массами без учета сил сопротивления (рис. 6.11). Рассматриваемая система обладает n степенями свободы, будет иметь n частот собственных колебаний ω1,ω2 ,Kωn , которым соответствуютn форм коле-
баний.
y
m1 |
|
m2 |
|
|
1 |
|
|
|
y |
2 |
|
m1 |
|
y |
|
I1 |
m2 |
||
|
|||
|
I2 |
||
|
|
mi
y i
mi

 Ii
Ii
mn x
y n
mn

 In
In
Рис. 6.11
Полные перемещения масс под действием инерционных сил I1, I2 ,K, In можно представить в виде:
y |
=δ |
I |
+δ |
I |
+δ |
I |
|
+K+δ |
I |
; |
|
1 |
11 |
1 |
12 |
2 |
13 |
|
3 |
1n |
n |
|
|
y2 |
= δ21I1 +δ22 I2 |
+δ23 I3 +K+δ2n In ; |
(6.30) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
K K K K K K K K |
|
|
|||||||||
|
=δn1I1 +δn 2 I2 +δn3 I3 +K+δn n In |
|
|||||||||
yn |
|
||||||||||
где δi i , δi k , Ii – соответственно перемещения точек расположения масс, вы-
званные силами P =1 и инерционные силы этих масс.
Так как силы инерции Ii = −mi yi″, то уравнения (6.30) можно записать
149
δ m y |
″ |
+δ |
m |
y |
|
|
″ |
+δ m y |
|
″ |
+K+δ |
|
|
m y |
n |
″ |
|
+ y |
= 0; |
|
||||||||||||
|
11 1 1 |
12 |
|
|
2 |
|
|
2 |
13 3 |
3 |
|
1n |
|
n |
|
|
|
1 |
|
|
|
|
||||||||||
|
|
″ |
+δ |
|
|
m |
|
y |
|
″ |
+δ |
m y |
|
″ |
+K+δ |
|
|
|
m y |
|
″ |
+ y |
|
|
= 0; |
|
||||||
δ m y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.31) |
||||||||||||||||
|
21 1 1 |
|
22 |
|
2 |
|
|
|
2 |
|
23 3 |
|
3 |
|
2 n |
|
n |
|
n |
|
|
|
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K K K K K K K K K K K K K |
|
|||||||||||||||||||||||||||||||
|
|
″ |
+δ |
|
|
|
m |
y |
″ |
+δ |
m y |
″ +K+δ |
|
|
|
m |
y |
|
″ + y |
|
= 0. |
|
||||||||||
δ m y |
n 2 |
n n |
n |
n |
|
|||||||||||||||||||||||||||
|
n1 1 1 |
|
2 |
|
|
|
2 |
|
n3 3 |
|
3 |
|
|
n |
|
|
|
|
|
|
|
|||||||||||
Уравнения (6.31) допускают следующие частные решения:
y1 = A1 sin(ω t +ϕ);
y2 = A2 sin(ω t +ϕ);
K K K K
yn = An sin(ω t +ϕ).
Вторые производные этих решений имеют вид:
|
|
|
y |
″ |
= −A ω2 sin(ω t |
+ϕ); |
|
|
|
|
|
||||||||||||
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
″ |
= −A2ω |
2 |
|
sin(ω t +ϕ); |
|
|
|
|
|
||||||||
|
|
|
y2 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
K K K K |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
″ |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= −Anω sin(ω t +ϕ). |
|
|
|
|
|
|||||||||||
|
|
|
yn |
|
|
|
|
|
|||||||||||||||
Подставив выражения |
|
y1, |
y2 , K, |
|
yn и их вторые производные в урав- |
||||||||||||||||||
нение (6.31), сократив на sin(ω t +ϕ) |
|
и сгруппировав слагаемые, получаем |
|||||||||||||||||||||
систему однородных уравнений в следующем виде: |
|
|
|
|
|||||||||||||||||||
|
|
−1)A1 |
+δ12m2ω |
|
A2 +K+δ1n mnω |
|
An = 0 |
|
|||||||||||||||
(δ11m1ω |
2 |
2 |
2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
δ m ω2 A |
+ (δ |
|
m ω2 −1)A |
+K+δ |
|
m ω2 A |
= 0 |
(6.32) |
|||||||||||||||
21 1 |
|
1 |
|
|
22 |
|
2 |
|
|
|
|
2 |
|
|
2 n |
|
n n |
|
|||||
K K K K K K K K K K K K |
|
||||||||||||||||||||||
δ m ω2 A |
+δ |
1n |
m ω |
2 A +K+ (δ |
n n |
m ω2 |
−1)A |
= 0 |
|
||||||||||||||
n1 1 |
|
1 |
|
|
2 |
2 |
|
|
|
|
|
n |
|
|
|
n |
|
|
|||||
Уравнения (6.32) |
будут |
справедливы, |
если |
принять все амплитуды |
|||||||||||||||||||
A 1, А 2, K А n равными нулю. Но в этом случае нет перемещений масс, сис-
тема находиться в покое на линии равновесия, и колебания отсутствуют. Если полагать, что амплитуды отличны от нуля, то такое решение возможно, когда определитель из коэффициентов при амплитудах равен нулю. Это является исходным условием для определения частот собственных колебаний системы.
150
