
Строительная механика
.pdf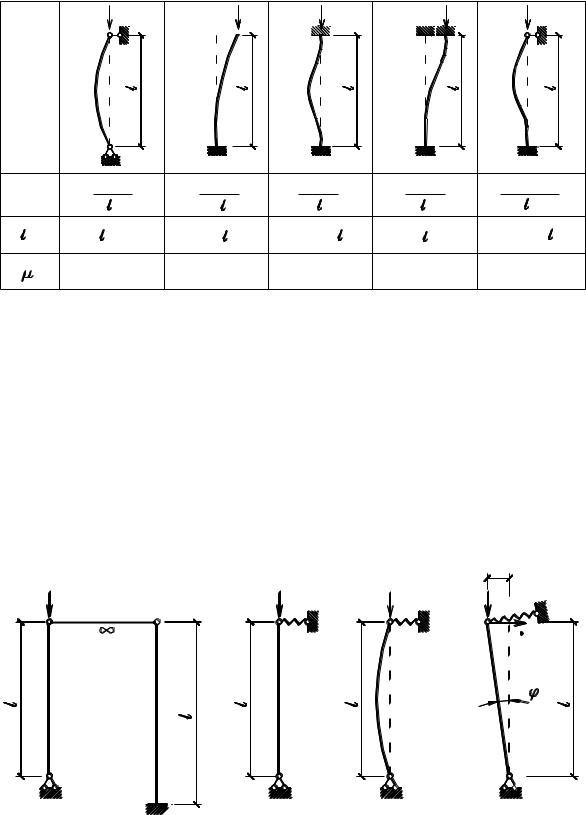
|
|
|
|
Таблица 5.1 |
Ркр |
Ркр |
Ркр |
Ркр |
Ркр |
Схема
стержня
Ркр |
2 |
EI |
2 EI |
4 2 EI |
2 EI |
20.19EI |
|
|
2 |
4 |
2 |
2 |
2 |
2 |
|
o |
|
|
2 |
|
0.5 |
|
0.7 |
|
1 |
|
2 |
|
0.5 |
1 |
0.7 |
Все формулы критических нагрузок, приведенные в таблице 5.1, получены статическим методом и позволяют получить точные значения критических сил.
5.7.Устойчивость стержней постоянного сечения с упругими опорами
На рис. 5.14а приведена стержневая система, в состав которой входит стойка АВ с обоими шарнирными концами, нагруженная силой P .
а)
Р
B EI2= |
D |
EI EI1
A
C
|
б) |
в) |
|
г) |
f |
|
I |
|
|||
|
Р |
|
|
Ркр |
|
|
|
Ркр |
|
||
|
B |
|
B |
B |
c f |
|
|
|
|||
|
Расчетная |
EI |
EI |
|
|
|
|
|
|
||
|
схема |
|
|
|
d |
1 |
EI |
|
|
|
|
|
|
|
|
||
|
A |
|
A |
|
A |
Рис. 5.14
Нижняя опора стойки AB шарнирно неподвижная, а верхним шарни-
91
ром B она соединена с остальной системой. Верхняя опора этой стойки может перемещаться в горизонтальном направлении ввиду податливости системы в целом. Если пренебречь продольными деформациями стержня BD ввиду их малости в сравнении с деформациями изгиба стержня CD (условно принято EI2 = ∞ ), то перемещение верхней опоры B будет определяться уп-
ругим изгибом стержня CD . Опорные закрепления такого характера принято называть упруго податливыми, и обозначаются они условно в виде пружины (рис. 5.14б), обеспечивающей упругое линейное смещение опоры.
В рассматриваемом случае мы имеем упругую линейно податливую опору и возможная форма потери устойчивости, соответствующая меньшему значению критической нагрузки, зависит от жесткости при изгибе EI нагруженного стержня AB и жесткости упругой опоры, роль которой играет стержень CD . При решении конкретных задач отыскивается наименьшее значение критической нагрузки, которое принимается в качестве расчетного.
При большой жесткости упругой опоры (пружины) и малой жесткости сжимаемого стержня AB, потеря устойчивости может произойти в форме изгиба этого стержня без горизонтального перемещения его верхней опоры (рис. 5.14 в). В этом случае критическая сила определяется по формуле Л.
Эйлера (5.12).
При малой жесткости (большой податливости) упругой опоры и большой жесткости нагруженного стержня AB он может потерять устойчивость, поворачиваясь на некоторый угол dϕ , оставаясь прямолинейным (рис. 5.14г).
Рассмотрим эту форму потери устойчивости и для определения критической нагрузки воспользуемся энергетическим методом. Пусть при потере устойчивости стержень AB повернулся на некоторый угол dϕ , как показано на рис. 5.14г и опора B переместилась по горизонтали на величину f . Опреде-
лим работу внутренних и внешних сил, выполненную ими при переходе системы в новое деформированное состояние. Обозначим C – жесткость упругой опоры, определяемая силой, необходимой для перемещения этой опоры
92
на единицу. К шарниру B приложены две силы: Pкр – по вертикали и C f –
по горизонтали. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Работа внутренних сил |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
U = |
|
1 |
C f f = |
1 |
C f 2 , |
|
|
|
|
|
|
||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
где C f – сила, необходимая для смещения опоры на величину |
f . |
|||||||||||||||||||||
Работа, выполненная внешней нагрузкой (формула 5.21), T = Pкрδ . |
||||||||||||||||||||||
На основании зависимости (5.20) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
1 l |
|
|
|
1 l |
|
|
|
|
|
1 l |
f 2 |
1 f 2 |
|
f |
2 |
|
|||||
δ = |
∫(y′)2 dx = |
|
∫tg2dϕ dx = |
|
∫ |
|
|
dx = |
|
|
l = |
|
|
. |
||||||||
2 |
|
|
2 l2 |
2l |
||||||||||||||||||
|
2 0 |
|
|
|
0 |
|
|
|
|
|
2 0 |
l |
|
|
||||||||
Тогда T |
= P |
f 2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
кр |
2l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По условию (5.15) |
Cf 2 |
= P |
f 2 |
, откуда |
|
|
|
|
|
|
||||||||||||
|
2 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
кр |
2l |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
Pкр = Сl . |
|
|
|
|
|
|
|
|
|
|
(5.27) |
|||
Поскольку действительная форма потери устойчивости заранее неизвестна, то для стержней с расчетной схемой, изображенной на (рис. 5.14б), критические силы определяют по формулам (5.12) и (5.27), а в качестве расчетного принимают меньшее значение из этих нагрузок.
Для определения критической нагрузки по формуле (5.27) необходимо отыскать жесткость упругой опоры, значение силы C , при которой перемещение этой опоры будет равно единице. Это перемещение может быть найдено по формуле Мора, а именно:
∆ip = ∑∫ |
|
M |
i M pdx |
. |
(5.28) |
|
|
EI |
|||
|
|
|
|
|
Например, в нашем случае эпюры изгибающих моментов от силы C в заданном состоянии и от P =1 во вспомогательном состоянии показаны соответственно на рис. 5.15а, б.
93
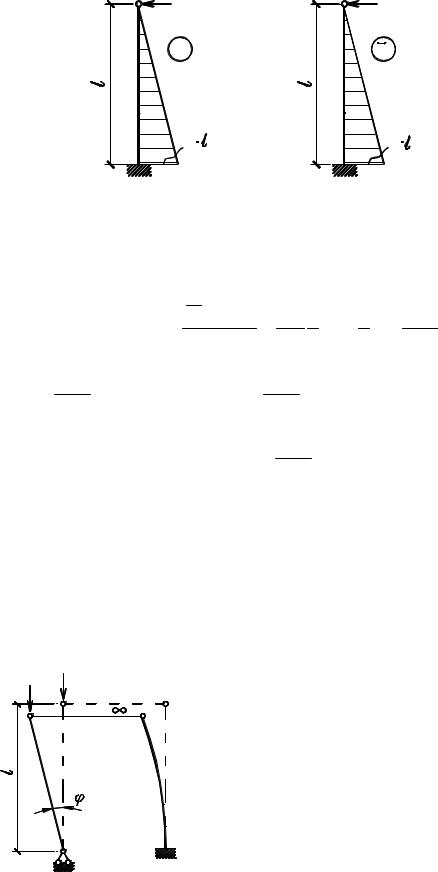
|
|
а) |
c |
|
|
|
|
|
|
|
|
|
|
|
|
б) |
P=1 |
|
||
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
MC |
|
|
|
|
|
|
|
|
|
|
|
|
MD |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
EI1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
EI1 |
|
|
|
|
|
|
C |
|
|
c |
|
1 |
|
|
|
|
|
|
|
C |
|
1 |
1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Рис. 5.15 |
|
|
|
|
|
|||||
Перемещение шарнира D , |
и такое же будет перемещение шарнира B , |
|||||||||||||||||||
( EI2 = ∞) в горизонтальном направлении |
|
|
|
|
|
|
||||||||||||||
|
|
f |
|
= ∑ |
|
M |
|
M |
|
dx |
= |
1 |
1 |
Cl l |
2 |
l = |
Cl3 |
|||
|
|
D |
∫ |
|
|
D |
|
|
C |
|
|
|
|
|
1 . |
|||||
|
|
|
|
|
|
EI1 |
|
|
EI1 2 |
1 1 |
3 |
1 |
3EI1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Из условия |
Cl3 |
|
|
|
|
|
|
|
|
C = |
3EI |
1 |
и по формуле (5.27) находим: |
|||||||
1 =1 получаем |
|
|
|
|
l3 |
|||||||||||||||
|
|
3EI1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
= Cl |
= |
3EI1 l . |
|
|
(5.29) |
||||||
|
|
|
|
|
|
|
|
кр |
|
|
|
|
l |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
Если в рассмотренной задаче конкретизировать решение и принять, на- |
||||||||||||||||||||
пример, EI1 = 2EI , а l1=l, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
P |
= Cl = 3 2EI l = 6EI < π 2EI = 9,86EI (по формуле (5.12)). |
|||||||||||||||||||
кр |
l3 |
|
l2 |
|
|
|
l2 |
|
|
l2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
При принятых значениях EI1 и l1 расчетной будет критическая нагруз- |
||||||||||||||||||||
|
PКР |
Р |
|
|
|
|
|
|
|
|
|
|
ка, |
найденная по формуле (5.27), а |
||||||
|
|
|
|
|
|
|
|
|
|
|
возможная форма потери устойчиво- |
|||||||||
|
B |
EI2 = |
|
D |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
сти показана на рис. 5.16. Формулу |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
EI |
|
|
2EI |
|
|
|
|
|
|
|
|
(5.27) можно представить в ином ви- |
|||||||
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
де. Если учесть принятое определе- |
||||||||
|
|
A |
|
C |
|
|
|
|
|
|
|
|
ние |
жесткости |
упругой опоры, то |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
можно записать |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Рис. 5.16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
94

Cδ11 =1, (5.30)
где δ11 – перемещение упруго податливой опоры в горизонтальном направ-
лении, вызванное силой P =1. Тогда:
C = |
1 |
и |
P |
= Сl = |
l |
. |
(5.31) |
|
|
||||||
δ11 |
|
кр |
δ11 |
|
|||
|
|
|
|
||||
При определении критической силы по формуле (5.31) достаточно построить эпюру от силы P =1, приложенной в направлении возможного перемещения упругой опоры и определить перемещение по формуле
∑∫ M12dx , что упрощает расчет.
EI
Упругой опорой может быть один стержень, несколько взаимосвязанных одиночных стержней или же часть статически определимой или неопределимой системы, к которой примыкает нагруженный стержень. В последнем случае при определении жесткости упругой опоры эпюра грузового состояния M c должна быть построена в заданной статически неопределимой сис-
теме. Эпюра вспомогательного состояния M i может быть взята в любой ста-
тически определимой основной системе метода сил. Если используется формула (5.31), то эпюру изгибающих моментов от силы P =1 необходимо построить в заданной статически неопределимой системе.
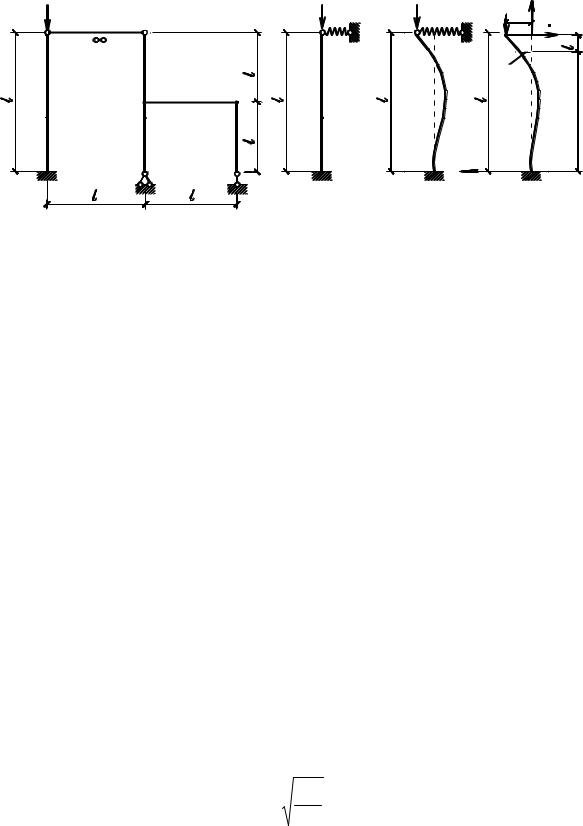
На рис. 5.17а приведена стержневая система, в которой нагруженная стойка AB постоянного сечения имеет одну защемленную опору, а вторая опора линейно податливая, допускающая упругое перемещение в горизонтальном направлении. Расчетная схема нагруженной стойки AB показана на рис. 5.17б.
95
а) |
Р |
|
|
б) |
Р |
B |
EI1= |
D |
|
|
B |
|
|
EI |
|
/2 |
|
|
|
|
|
|
|
EI |
|
|
|
|
EI |
|
|
|
kEI |
|
|
|
|
EI |
EI |
/2 |
|
|
|
|
|
||
A |
|
C |
E |
|
A |
|
|
|
|
в) Р |
г) Ркр f |
x |
|
|
|
|
c f |
B |
B |
|
-x |
|
|
y |
|
|
|
|
x |
A |
y |
A o |
|
Рис. 5.17
В этом случае стержень AB не может перейти в новое деформированное состояние (новое положение равновесия), оставаясь прямолинейным, так как защемляющая опора не допускает свободного угла поворота. При линейном перемещении опоры B стержень будет изгибаться (рис. 5.17в). Рассмотрим деформированное состояние стержня под действием критической нагрузки и определим эту нагрузку статическим методом, пользуясь дифференциальным уравнением равновесия − EIy′′ = M x (5.4). В деформированном состоянии на стержень действует критическая нагрузка Pкр , стремящаяся увеличивать де-
формации его изгиба и сила со стороны упругой опоры C f , препятствую-
щая его отклонению от начального положения равновесия (рис. 5.17г). Изгибающий момент в произвольном сечении стержня
|
M x = −Pкр(f − y)+ C f (l − x). |
||||
Тогда |
EI y′′ = Pкр(f − y)− C f (l − x), |
|
|||
или |
EI y′′ + Pкр y = Pкр f − C f (l − x). |
||||
Разделив слагаемые последнего равенства на EI и обозначив |
|||||
|
n = |
Pкр , |
|
(5.32) |
|
|
|
EI |
|
|
|
дифференциальное уравнение принимает вид: |
|||||
|
|
|
|
C |
|
|
y′′ + n2 y = f |
n2 |
− |
|
(l − x) . |
|
EI |
||||
|
|
|
|
|
|
Решение этого уравнения
96
|
y = Asin(nx)+ Bcos (nx)+ f 1 − |
|
C |
|
|
(l − x) . |
|||||||||||||
|
|
2 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
n |
EI |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
Для определения A, |
B и |
f используем граничные условия: |
|||||||||||||||||
1) при x = 0, y = 0; |
|
|
2) при x = l, y = f ; |
|
|
|
|
|
3) при x = 0, y′ = 0 . |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C l |
||||
По первому условию |
y = A 0 + B 1+ |
f 1− |
|
= 0. |
|||||||||||||||
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n2EI |
||||
По второму условию |
|
y = A sin (nl)+ B cos(nl)+ f = f . |
|||||||||||||||||
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
C |
|
|
По третьему условию |
y |
= A n cos (nx)− B n sin(nx)+ f n2 EI . |
|||||||||||||||||
|
|||||||||||||||||||
При x = 0 |
|
′ |
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
||
y |
= A |
n 1 − B n 0 + f n2 EI = 0 . |
|
|
|
|
|||||||||||||
|
|
|
|
|
|||||||||||||||
Система однородных линейных уравнений имеет вид:
|
|
|
|
|
C l |
|
|||
A 0 |
+ B 1 |
+ f 1 − |
|
|
|
= 0; |
|||
|
|
||||||||
|
|
|
|
|
n2 EI |
|
|||
|
|
|
|
|
|
|
|
|
|
A sin (nl)+ B cos (nl)+ C 0 = 0; |
|||||||||
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
+ f |
2 |
|
= 0. |
|
||||
A n + B 0 |
|
|
|||||||
|
|
|
n |
|
EI |
|
|||
По условию (5.3) получаем характеристическое уравнение:
|
|
|
|
− |
C l |
|
|
||
|
0 |
1 |
1 |
|
|
|
|
||
|
|
||||||||
D = |
sin (nl) |
cos (nl) |
|
|
|
n2 EI |
= 0 . |
||
|
|
|
0 |
|
|
||||
|
n |
0 |
|
|
|
C |
|
|
|
|
|
|
n2 EI |
|
|
||||
|
|
|
|
|
|
|
|||
Раскрыв определитель, имеем:
|
|
C l |
|
C |
|
|
− n cos (nl) 1 |
− |
|
|
− |
|
sin (nl)= 0 . |
|
n2 EI |
|||||
|
|
n2 EI |
|
|
||
Разделив слагаемые последнего равенства на cos (nl ), раскрыв скобки и преобразовав, получаем уравнение устойчивости в следующем виде:
tg(nl)= nl − (nl)3 EI . |
(5.33) |
C l3 |
|
Уравнение (5.33) решается путем подбора такого значения параметра
97

nl , при котором выполняется равенство. Если такое значение nl найдено, то по условию (5.32)
P = n2EI . |
(5.34) |
кр |
|
Выявим границы, в пределах которых могут находиться значения параметра nl и Pкр .
Если C = 0, tg(nl)= −∞ , nl = −π |
и P |
= π 2 EI |
(случай, когда |
|
2 |
кр |
4l 2 |
|
|
|
|
|
||
нижний конец стойки защемлен, а верхний свободный).
Если C = ∞, tg(nl )= nl, nl = 4,493 и P = 20,19EI , что соответст-
кр |
l 2 |
|
вует условию, когда нижний конец стойки защемлен, а верхний шарнирно оперт. Оба эти граничные значения критических сил соответствуют формулам Л. Эйлера (табл. 5.1). В рассматриваемом примере предельные значения параметра nl и критической нагрузки определяются условиями:
1,57 ≤ nl ≤ 4,493; |
|
|
|
|||||
|
|
|
≤ P |
≤ |
20,19EI . |
5.34а |
||
π 2 EI |
||||||||
|
|
|
кр |
|
|
|
|
|
4 l |
2 |
|
l |
2 |
|
|||
|
|
|
|
|
|
|
||
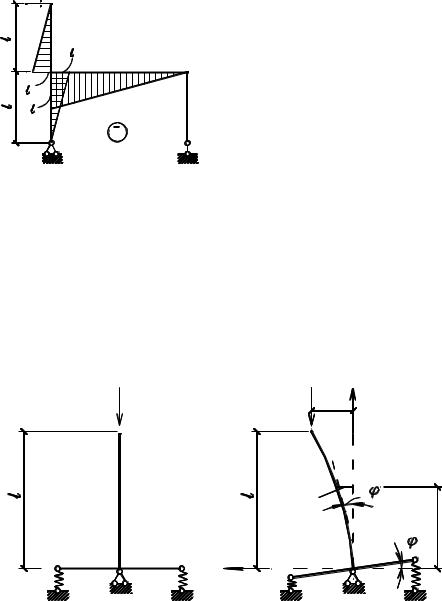
Проследим ход решения такого типа задач на примере рассмотренной выше системы (5.17а). Роль упругой опоры играет рама СDЕ. Расчетная схема нагруженной стойки приведена на рис. 5.17б. Построив эпюру изгибающих моментов при действии силы P =1 (рис. 5.18), горизонтальное перемещение узла C (такое же перемещение будет и опоры В) найдем по формуле
|
|
|
2dx |
|
|
M |
|
||
δ11 = ∑∫ |
1 |
способом перемножения эпюр. Пользуясь зависимостью |
||
|
||||
|
|
EI |
|
|
(5.30), определим характеристику упругой опоры C = 1 .
δ11
98
|
Р=1 |
C |
Подставив выражение характеристи- |
|
|
ки упругой опоры (С) в уравнение |
|
/2 |
|
|
|
|
|
/2 |
(5.33), отыскиваем (пользуясь 5.34а) |
|
|
|
|
/2 |
/2 |
|
значение nl , при котором удовлетворя- |
|
|
M1 |
ется уравнение (5.33), а затем по фор- |
|
|
E |
|
|
|
D |
|
|
|
|
муле (5.34) находим значение критиче- |
|
|
Рис. 5.18 |
скойсилы. |
На рис. 5.19а изображен центрально нагруженный стержень с верхним |
|||
свободным и нижним упруго защемленными концами. Предполагается, что в |
|||
упруго-защемляющей опоре средний узел B остается линейно неподвижным, |
|||
в то время как узлы A и C могут перемещаться в вертикальном направлении, |
|||
ввиду упругой податливости опорных частей этих узлов. |
|||
|
а) |
Р |
|
б) |
Ркр |
f |
x |
|
|
|
|
|
|
|
|
EI |
d |
|
|
|
|
EI |
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
y |
|
|
|
o kEI |
d |
k =∞ |
A |
|
|
|
A |
|
C |
|||
kEI |
B kEI |
C |
|
kEI |
B |
|
|
||
|
|
|
|
|
|
Рис. 5.19
Рассмотрим этот стержень в деформированном состоянии под действием критической нагрузки. Решение задачи выполним статическим методом. Обозначим через C жесткость упруго защемленной опоры В, определяемую моментом, необходимым для поворота этой опоры на угол, равный единице. Дифференциальное уравнение равновесия примем в виде:
− EIy′′ = M x .
Изгибающий момент в произвольном сечении
M x = −Pкр(f − y) и EIy′′ + Pкр y = Pкр f .
Разделив все слагаемы последнего равенства на EI и обозначив
99

n = |
Pкр |
|
′′ |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EI , получаем y |
+ n |
y = n |
f . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Решение этого уравнения имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
y = A sin(n x)+ B cos(n x)+ f . |
|
|
(5.35) |
||||||||||||||||
|
Для определения постоянных в уравнении (5.35) воспользуемся гра- |
||||||||||||||||||||||||||
ничными условиями: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1) при x = 0, |
y = 0; |
|
|
|
|
|
2) при x = l, |
|
y = f ; |
|
|
3) при x = 0, y′ = |
M3 |
||||||||||||||
|
|
|
|
|
|
|
|
|
, |
||||||||||||||||||
|
|
|
|
|
|
|
C |
||||||||||||||||||||
где |
M 3 – момент в защемляющей опоре, равный Pкр f . |
|
|
|
|
||||||||||||||||||||||
|
По первому условию |
|
|
y = A 0 + B 1 + f 1 = 0 . |
|
|
|
|
|||||||||||||||||||
|
По второму условию |
|
|
y = A sin(nl)+ B cos(nl)+ f = f . |
|
|
|||||||||||||||||||||
|
По третьему условию |
|
|
y′ = A ncos(n x)− B nsin(n x). |
|
|
|||||||||||||||||||||
|
При x = 0, |
|
y |
′ |
= A n |
1 − B 0 = |
Pкр f |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
C |
, |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
n |
2 |
EI |
|
|
|
P |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кр |
|
|
|
|||||
или |
|
|
|
y |
|
= A n |
− B 0 − |
f |
|
C |
|
|
= 0, |
n = |
EI |
. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Линейные уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
0 + B |
1 + f 1 = 0; |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
sin(nl)+ B cos(nl)+ f 0 = 0; |
|
|
|
|
||||||||||||||||
|
|
|
|
A |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 EI |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
n − B |
|
0 − f |
|
= 0. |
|
|
|
|
|
|
||||||||||
|
|
|
|
A |
|
C |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
По условию (5.3) получаем характеристическое уравнение в виде: |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
D = |
sin(nl) |
cos(nl) |
|
|
|
0 |
|
|
= 0, |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
n |
|
0 |
|
|
|
|
− |
n2 EI |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
откуда |
− ncos(nl)+ sin(nl) |
n2 EI |
= 0 , |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100
