
Строительная механика
.pdf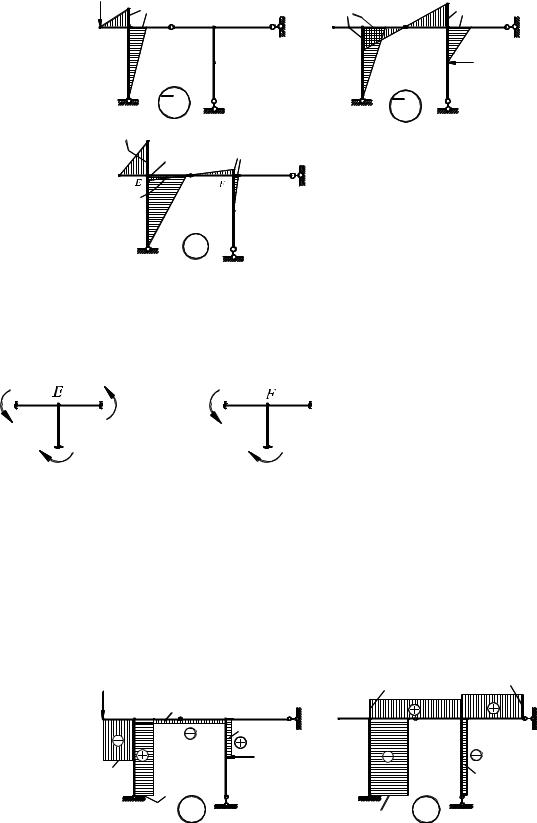
а) I1= 0,1823 |
б) |
|
0,3646 |
0,6435 |
0,6435 |
I 2= 0,2574
в) |
M1I1 |
M2I 2 |
4,3646 |
|
|
|
0,6435 |
0,6435 |
|
5,008 |
|
|
MD |
|
Рис. 6.16
Правильность построения эпюры M D состоит в проверке равновесия узлов системы. Проверяем равновесие узлов E и F (рис. 6.17):
|
0,6435 |
Равновесие узлов E и F. |
|
∑M E = 5,008 −0,6435 − |
|
4,3646 |
0,6435 |
|
|
|
− 4,3646 = 0. |
5,008 |
|
0,6435 |
|
Рис. 6.17 |
∑M F = 0,6435 − 0,6435 = 0. |
|
|
С помощью эпюры M D обычными приемами находятся значения по-
перечных сил, а затем из условий равновесия узлов находятся продольные силы в стержнях системы. Эпюры QD и N D приведены на рис. 6.18.
а) |
б) |
1,2594 |
I1= 0,1823 |
1,002 |
|
0,2145 |
|
|
|
0,2574 |
|
2,1823 |
I 2= 0,2574 |
0,2145 |
|
||
1,002 |
|
|
QD |
1,9678 |
ND |
|
|
|
|
Рис. 6.18 |
|
Для проверки их |
правильности можно |
использовать уравнения |
∑ X = 0 и ∑Y = 0, рассматривая равновесие системы в целом. В эти уравне-
161
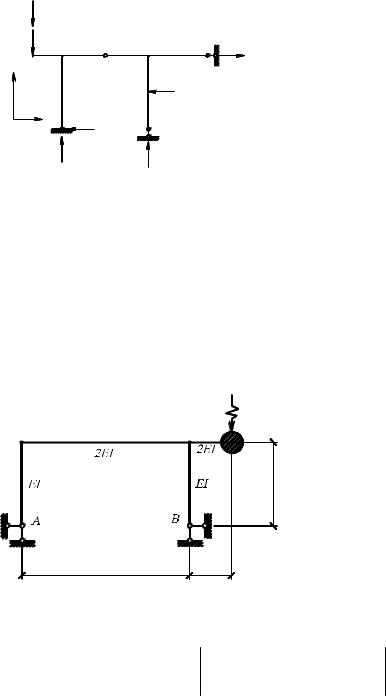
ния должны быть включены опорные реакции, найденные инерционные силы с учетом их знаков и действующие динамические нагрузки. Для рассматриваемой рамы указанные проверки приведены на рис. 6.19.
∑ X =1,2594 −0,2574 −1,002 =
I1 = 0,1823 |
|
=1,2594 −1,2594 = 0; |
|
|||
|
|
|
|
|||
P=2 кН |
1,2594 |
∑Y =1,9678 |
+ 0,2145 |
− 2 −0,1823 |
= |
|
|
|
|||||
|
|
|
||||
y |
|
|
= 2,1823 −2,1823 = 0. |
|
|
|
|
|
I2= 0,2574 |
|
|
||
|
|
|
|
|
|
|
x |
1,002 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1,9678 |
0,2574 |
|
|
|
|
|
|
Рис. 6.19 |
|
|
|
|
Расчет статически неопределимой рамы
Для заданной рамы (рис. 6.20) требуется определить динамические изгибающие моменты, поперечные и продольные силы и построить их эпюры при m = 0,5m ; Р = 2кН ; α = 0,6.
Psinθt
m
4м
8м |
2м |
Рис. 6.20
D = (δ11m − λ)
δ21m
С учетом принимаемых допущений (п. 6.1) масса m может перемещаться по вертикали и в горизонтальном направлении, а рассматриваемая система обладает двумя степенями свободы. Равенство (6.33) в этом случае принимает вид:
δ12m |
= 0, |
(δ22m − λ) |
откуда (δ11m − λ)(δ22 m − λ)−δ122 m2 = 0 . |
(6.43) |
|
В уравнении (6.43) |
δii ,δik – перемещения массы в заданной системе, |
|
вызванные статическими |
силами Pi =1, действующими |
по направлениям |
162
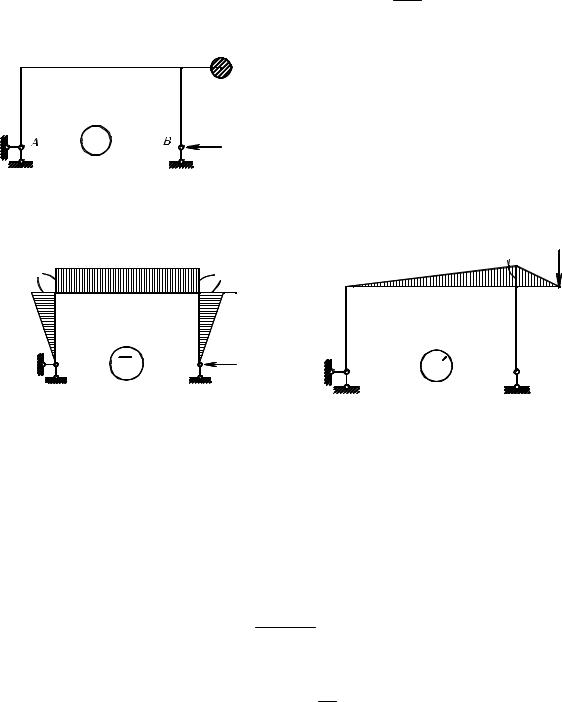
возможных перемещений этой массы.
Так как заданная система статически неопределима, то указанные перемещенияδi i и δi k должны быть найдены после раскрытия ее статической
неопределимости. Воспользуемся методом сил (основная система приведена на рис. 6.21). Каноническое уравнение и выражение неизвестного X1 :
δ |
X |
1 |
+ ∆ |
1 p |
= 0; X |
1 |
= −∆1 p . |
(6.44) |
11 |
|
|
|
δ |
|
|||
|
|
|
|
|
|
|
11 |
|
|
|
|
m |
|
Эпюра изгибающих моментов от дей- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ствия силы X 1 =1 приведена на рис. |
|||
O.C. |
x1 |
|
|
6.22, а от вертикальной силы P1 =1 – |
||||
|
|
|
|
|
|
|||
на рис 6.23.
Рис. 6.21
4 |
4 |
x1 =1 |
M1 |
2 |
P1 |
=1 |
|
||
MP |
|
|
|
Рис. 6.22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.23 |
|
|
|
|
|
|||||
|
|
|
|
|
2dx |
|
|
|
1 1 |
|
|
2 |
|
|
|
|
|
1 |
|
|
|
128 |
|
64 |
|
320 |
|
||||||
|
= ∑∫ |
M |
= |
|
4 4 |
4 |
2 + |
|
|
|
|
|
|
||||||||||||||||||||
δ11 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
4 8 4 = |
|
+ |
|
= |
|
. |
|||||||||||||
|
|
EI |
|
EI 2 |
3 |
2EI |
3EI |
EI |
3EI |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
1M |
′p dx |
|
|
|
1 |
1 |
|
|
|
|
16 |
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
|
∑∫ |
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
∆1 p |
= |
|
|
|
|
|
|
|
= |
|
|
|
|
|
2 |
8 4 |
= |
|
. |
|
|
|
|
|
|
||||||
|
|
|
|
|
EI |
|
|
2EI |
2 |
EI |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
По формуле (6.44) имеем
X1′ = −16EI 3320EI = −0,15.
Окончательная эпюра изгибающих моментов (M1 ), полученная по условию
M1 = M ′p + M1X1′,
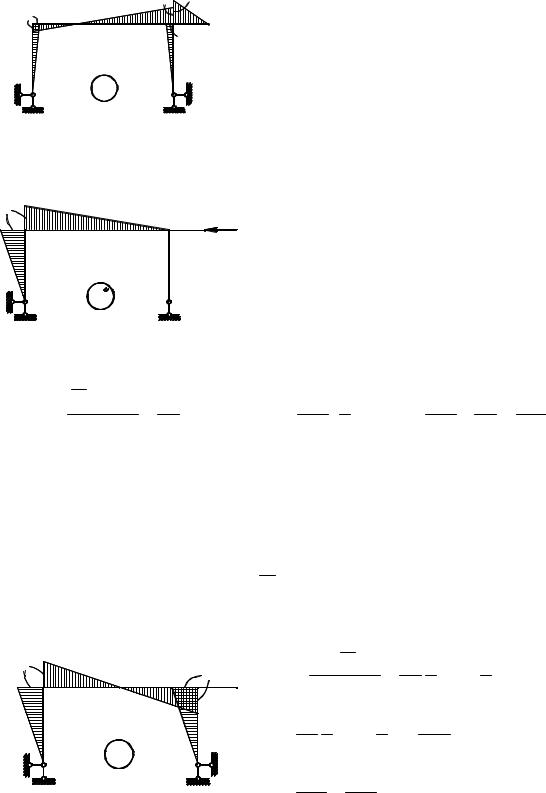
приведена на рис. 6.24.
163
1,4 |
2 |
0,6 |
|
|
0,6 |
M1 |
|
Рис. 6.24
Кинематическая проверка правильности этой эпюры (M1 ):
∑∫ |
M |
1 |
|
M 1 |
dx |
= − |
1 1 |
4 |
4 |
2 |
0,6 2 + |
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
EI |
|
EI 2 |
3 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
+ |
1 |
|
|
4 8 |
1,4 − 0,6 = − |
6,4 |
+ |
6,4 |
= 0. |
||||||||||
2 EI |
EI |
EI |
|||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||
4 |
|
|
|
|
|
|
|
|
Эпюра |
|
изгибающих моментов в ос- |
|||||||||
|
|
|
|
|
P2 =1 |
|
|
новной системе от действия горизон- |
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
тальной силы P2 |
=1 приведена на рис. |
||||||||||
|
MP |
|
|
|
|
|
|
|
6.25. Перемещение, вызываемое этой |
|||||||||||
|
|
|
|
|
|
|
|
|
нагрузкой |
|
|
|
|
|
|
|||||
|
Рис. 6.25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∆1′′p = ∑∫ |
M1M |
′p′dx |
= |
1 1 |
4 4 |
2 |
4 |
|
+ |
1 |
|
1 |
4 8 4 |
= |
64 |
+ |
32 |
= |
160 |
|
EI |
EI 2 |
3 |
|
2EI |
2 |
3EI |
EI |
3EI |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
По условию (6.44) |
X 1′′= − |
160 3EI |
|
= −0,5. |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
3EI 320 |
|
|
|
|
|
|
|
|
|
|
|
|||
Окончательная эпюра изгибающих моментов от горизонтальной нагрузки, полученная по условию
M 2 = M ′p′ + M 1 X 1′′,
приведена на рис. 6.26. Кинематическая проверка правильности этой эпюры:
2 |
2 |
|
M2 |
∑∫ M 2EIM1dx = EI1 12 2 4 234 −
− EI1 12 2 4 23 4 + 21EI 4 8 0 = = 332EI − 332EI = 0 .
Рис. 6.26
Статические проверки правильности окончательных эпюр M1 и M 2 не приводим в развернутом виде, так как легко убедиться, что они выполняются.
Перемещения, вызванные единичными силами в статически неопредели-
164
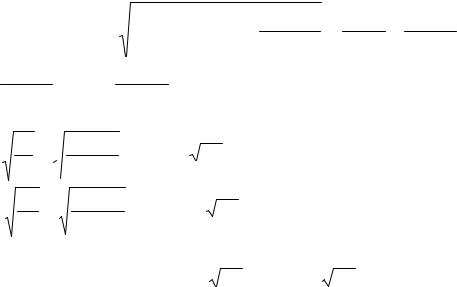
мой системе, будут:
|
|
|
δ11 |
= ∑∫ |
|
M |
2dx |
=∑∫ |
M1M ′p dx |
|
|
|
|
|
|
1 1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
2 |
8 |
|
|
|
|
1,4 |
− |
|
|
0,6 |
|
+ |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
EI |
|
|
|
|
|
|
|
|
|
|
EI |
|
|
|
|
|
2EI 2 |
3 |
|
3 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
+ |
|
|
1 |
|
|
|
|
1 |
|
2 2 |
|
2 |
2 = |
4,2667 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2EI 2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
δ22 = ∑ |
|
|
|
|
M 2 dx |
|
=∑∫ |
|
M 2 M ′p′dx |
= |
|
|
|
1 1 |
2 |
|
4 |
2 |
4 |
+ |
1 1 |
4 |
8 |
× |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
∫ |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
EI |
|
|
|
|
|
|
|
|
|
EI |
|
|
|
|
|
EI |
2 |
3 |
2EI 2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
16,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
× |
|
|
|
|
|
|
2 |
− |
|
|
|
|
|
|
2 |
= |
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
3 |
|
3 |
|
|
|
EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
δ12 =δ21 = ∑∫ |
|
M |
1 |
M |
2 |
dx |
=∑∫ |
|
M1M ′′p dx |
=∑ |
∫ |
|
|
M 2 M ′p dx |
= |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
EI |
|
|
|
|
|
|
|
|
|
|
|
EI |
|
|
|
|
|
|
|
|
EI |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2,6667 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
2 8 |
|
|
|
2 − |
|
|
|
2 |
= − |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2EI 2 |
3 |
3 |
|
|
|
|
EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Подставив |
|
|
найденные |
|
|
|
значения |
|
|
перемещений |
в |
|
|
уравнение (6.43), |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
4,2667 |
|
m − λ |
|
16,0 |
|
m − λ |
|
− |
|
− |
|
2,6667 |
2 |
m |
2 |
= 0, |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
получаем |
|
EI |
|
|
|
|
EI |
|
|
|
|
|
|
|
|
EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
откуда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||
4,2667 |
m |
16,0 |
m − |
4,2667 |
m λ − |
16 |
mλ + λ |
2 |
|
− |
|
|
|
2,6667 |
m |
2 |
= 0; |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
EI |
|
|
EI |
|
|
|
|
|
|
|
EI |
|
|
|
|
|
EI |
|
|
− |
|
|
|
EI |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
λ2 − |
20,267 |
mλ + |
75,378 |
|
m 2 = 0; λ |
2 |
|
− |
10,134 |
λ + |
|
|
18,845 |
= 0 . |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
EI |
|
|
|
|
|
|
(EI )2 |
|
|
|
|
|
|
|
|
|
EI |
|
|
|
|
|
|
(EI )2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Корни этого равенства: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
λ |
|
|
|
|
|
|
10,134 |
± |
|
|
|
|
− |
10,134 |
2 |
− 4 |
|
18,845 |
|
= |
|
5,067 |
± |
2,6133 |
; |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
= − |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(EI )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
2EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
EI |
|
|
EI |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
1,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
λ1 = 7,6803EI и λ2 = 2,4537EI .
Частоты собственных колебаний:
ω1 = λ1 = EI = 0,3608 EI (c−1 ); 1  7,6803
7,6803
ω2 = |
1 |
= |
EI |
= 0,63839 |
EI (c−1 ). |
|
λ2 |
|
2,4537 |
|
|
Частота вибрационной нагрузки (при α =0,6): |
|||||
θ =αωmin |
= 0,6 ω1 = 0,6 0,3608 |
EI = 0,21648 EI (c−1 ). |
|||
Эпюра изгибающих моментов от статического действия амплитудного
165
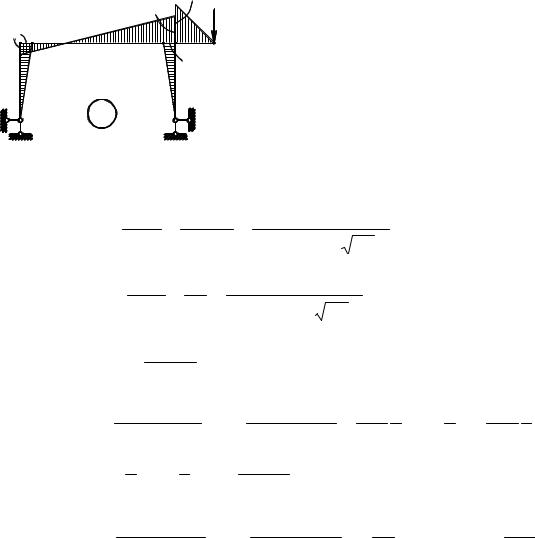
значения вибрационной нагрузки при P = 2 кН, получаемая по условию
|
|
|
|
|
|
|
|
|
|
|
M стP = M1 P , |
|
|
|
|
|
|
|
|
||||||
приведена на рис. 6.27. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
2,8 |
|
|
4 |
|
|
|
|
Максимальные |
значения |
инерцион- |
|||||||||
|
|
|
|
|
|
|
|
|
|
2 кН |
|
|
ных сил найдем, пользуясь уравне- |
||||||||||||
1,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
1,2 |
|
|
|
|
ниями |
(6.40). В нашем случае эти |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
уравнения |
|
имеют |
|
|
вид: |
|||||
MсPm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
+δ12 I2 + ∆1P = 0; |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ11I1 |
|
|
(6.45) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+δ220 I2 + ∆2P = 0, |
|
|
||||||
Рис. 6.27 |
|
|
|
|
|
|
|
|
δ21I1 |
|
|
|
|||||||||||||
где: |
|
|
|
|
1 |
|
4,2667 |
|
|
|
|
|
1 |
|
|
|
= −38,410 ; |
|
|
|
|||||
δ110 =δ11 |
− |
|
|
|
= |
− |
|
|
|
|
|
EI )2 |
|
|
|
||||||||||
|
|
|
mθ 2 |
|
|
|
EI |
|
0,5(0,21648 |
|
EI |
|
|
|
|||||||||||
δ220 =δ22 |
− |
|
|
|
1 |
= 16 |
− |
|
|
|
|
1 |
|
|
|
= −26,677 ; |
|
|
|
||||||
|
|
|
mθ 2 |
|
EI |
0,5(0,21648 EI )2 |
|
|
EI |
|
|
|
|||||||||||||
δ12 =δ21 = − |
2,6667 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆1P = ∑∫ M1 M стP dx |
= ∑∫ M P′ M стP dx |
= |
|
1 1 2 2 2 4 + |
1 1 |
2 |
|||||||||||||||||||
|
|
|
|
|
|
EI |
|
|
|
|
|
|
|
EI |
|
|
2EI 2 |
3 |
2EI 2 |
|
|||||
|
2 |
2,8 |
− |
1 |
|
|
|
8,5333 |
; |
|
|
|
|
|
|
|
|
|
|||||||
8 |
|
|
3 |
1,2 = |
|
|
EI |
|
|
|
|
|
|
|
|
|
|
||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
∆2P = ∑∫ M 2 M стP dx |
= ∑∫ M P′′ M стP dx = − 1 1 |
1,2 4 2 4 |
+ |
1 |
1 4 × |
||||||||||||||||||||
|
|
|
|
|
|
EI |
|
|
|
|
|
|
|
EI |
|
|
|
EI 2 |
3 |
|
2EI 2 |
||||
|
|
|
1 |
2,8 − |
2 |
|
|
|
|
5,3333 |
. |
|
|
|
|
|
|
|
|
||||||
×8 |
3 |
3 |
1,2 = − |
|
EI |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Подставив значения коэффициентов при неизвестных и свободных членов в уравнения (6.45) имеем:
− |
38,410 |
|
I1 |
− |
2,6667 |
|
I2 + |
8,5333 |
= 0; |
|
EI |
EI |
EI |
||||||||
|
|
|
|
|
|
|
||||
|
2,6667 |
|
|
|
26,677 |
|
|
5,3333 |
|
|
|
|
I1 |
|
|
I2 − |
= 0, |
||||
− |
|
|
− |
|
|
|
||||
EI |
|
EI |
|
EI |
||||||
|
|
|
|
|
|
|
откуда
166
I1 = 0,23769,
I2 = −0,22367.
Максимальные усилия в элементах рамы при установившихся вынужденных колебаниях будут:
M D = M стP + M1I1 + M 2 I2.
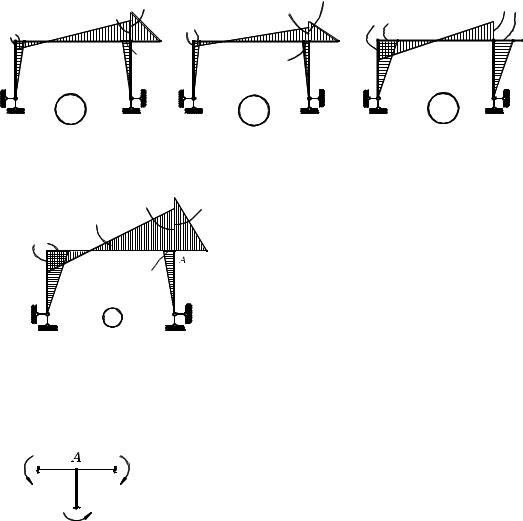
Эпюры изгибающих моментов от статического действия динамической нагрузки (M стр )и фактических значений инерционных сил (M i Ii ) приведены на рис. 6.28а,б,в, а окончательная эпюра динамических изгибающих моментов M D – на рис. 6.29.
а) |
4 |
б) |
0,44538 |
в) |
2,8 |
0,33277 |
|
0,44734 |
|
|
|
0,44734 |
||
1,2 |
|
0,14261 |
|
|
|
|
|
|
|
|
1,2 |
0,14261 |
|
|
|
|
|
|
|
MсPm |
|
M1I1 |
|
M2I2 |
|
|
|
Рис. 6.28 |
|
3,5801 |
4,4754 |
Проверки правильности построения |
|
|
|
|
|
0,89505 |
|
эпюры M D остаются обычными: ста- |
1,7900 |
|
|
|
|
|
|
|
|
0,89527 |
|
тическая и кинематическая. |
|
|
|
|
|
MD |
|
|
|
Рис. 6.29 |
|
|
Статическая проверка |
|
∑M A = 4,4754 − 3,5801 − 0,89527 = |
|
|
4,4754 |
|
= 4,4754 − 4,4754 = 0. |
3,5801 |
|
|
|
|
0,89527 |
|
|
167
Кинематическая проверка: ∑∫ M D M 1 dx = 0 .
EI
Эпюра M1 изображена на рис. 6.22 и, пользуясь правилом Верещагина,
имеем:
− EI1 121,79 4 23 4 + 21EI 4 8 0,89505 − EI1 12 0,89527 4 23 4 = −9,5467 + +14,321 − 4,7748 =14,321 −14,321 = 0.
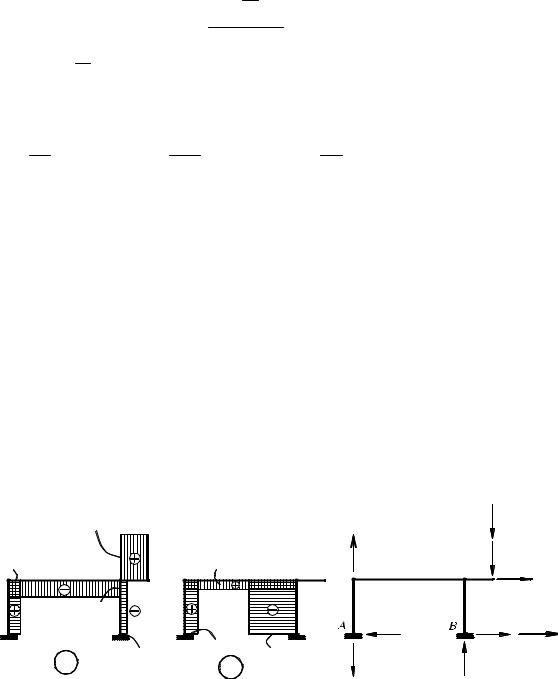
Поперечные и продольные силы, вызываемые динамическими нагрузками, строятся теми же приемами, что и в расчетах на действие статических нагрузок. С помощью эпюры M D строится эпюра QD , а затем из условия равновесия узлов находятся продольные силы в стержнях, и строится эпюра N D . Указанные эпюры приведены соответственно на рис. 6.30а,б. На рис. 6.30, в обозначены действующие на раму нагрузки и опорные реакции, включенные в уравнения равновесия ∑ X = 0 и ∑Y = 0 при выполнении проверок равновесия системы в целом.
а) |
2,2377 |
б) |
в) |
I1= 0,23769 |
|
|
|
y |
|
|
|
|
|
0,4475
0,67126 |
QD 0,22382
0,4475 |
|
|
0,67126 |
2,909 |
|
ND |
||
|
|
P=2 |
|
I2= 0,22367 |
H =0,4475 |
H = |
A |
B 0,22382 |
|
x |
VA =0,67126 |
VB =2,909 |
Рис. 6.30
∑X = 0; 0,22367 + 0,22382 − 0,4475 = 0,4475 − 0,4475 = 0.
∑Y = 0 ; 2,909 − 0,23769 − 2 − 0,67126 = 2,909 − 2,909 = 0.
∑МА = 0 ; − 2,909 8 + 0,23769 10 + 2 10 + 0,22367 4 = = −23,272 + 2,3769 + 20 + 0,89468 = −23,272 + 23,272 = 0
168
Глава 7
Приближенные методы и способы определения частот свободных колебаний
7.1. Назначение приближенных методов
Приведенные выше решения задач динамики сооружений выполнены статическим (кинетостатическим) методом, который с учетом принимаемых допущений считается точным методом. Расчет систем с большим числом степеней свободы статическим методом оказывается очень громоздким и трудным. Если в любой стержневой системе учесть собственный вес хотя бы одного из ее элементов, то получаем систему с бесконечным числом степеней свободы и решить задачу в такой постановке без замены распределенных масс сосредоточенными статическим методом невозможно. Это обстоятельство заставляет инженеров прибегать к приближенным методам и способам. Один из наиболее распространенных приемов упрощения решения состоит в замене распределенных масс заданной системы сосредоточенными (точечными) массами, т.е. осуществляется переход к системе с конечным числом степеней свободы, и решение может быть выполнено статическим методом. Этим решением будут получены приближенные значения частот свободных колебаний. Чем большее количество принято сосредоточенных масс, тем точнее получаемый результат, но в то же время сложнее расчет.
Для однопролетной шарнирно опертой балки постоянного сечения со сплошной по всему пролету равномерно распределенной массой (система с бесконечным числом степеней свободы) получено решение, позволяющее находить точное значение наименьшей (первой) частоты свободных колебаний системы (решение будет приведено ниже). Этим решением можно воспользоваться для определения наименьшей частоты свободных колебаний в других системах (например, в рамах), если позволяют условия заданной системы. Но это решение может быть применено для ограниченного круга задач. В общем случае в системах с числом степеней свободы, равным бесконечно-
169
сти, частоты свободных колебаний отыскиваются приближенными методами. Могут быть так же использованы свойства симметрии системы, если
это допускает заданная или преобразованная система.
Большое значение имеют те приближенные методы решения задач динамики, которые позволяют более простым путем получить результат достаточной точности с практической точки зрения.
Решение важной задачи динамики сооружений – нахождение частот свободных колебаний системы – существенно упрощается, если известны уравнения изгиба стержней при колебаниях системы. Уравнения изгиба стержней, как правило, неизвестны и в приближенных методах их принимают условно с учетом условий соединения между собой стержней в системе и закрепления их на опорах. Это наиболее трудный и ответственный этап в использовании приближенных методов, так как он предопределяет достоверность получаемого результата.
Широко используемый в расчетной практике способ замены распределенных масс сосредоточенными (точечными) массами дает удовлетворительную точность при определении первой (наименьшей) частоты свободных колебаний и может приводить к значительным погрешностям при вычислении высших частот.
Основным недостатком приближенных методов является то, что неизвестна степень точности (погрешности) полученного результата. Для наиболее часто используемых приближенных методов практическими расчетами выявлены общие критерии их точности (например, для энергетического метода), а в других случаях степень приближенности результата может быть установлена после решения той же задачи точным методом.
7.2. Энергетический метод
Ранее (п. 6.1) отмечалось, что в основу этого метода положен закон сохранения энергии, согласно которому в любой момент временно сума потенциальной и кинематической энергии колеблющейся системы остается посто-
170
