Строительная механика

сти формы его равновесия (деформаций). В первом случае система переходит в новое положение, сохраняя неизменной свою структуру по геометрическим параметрам, а во втором изменение формы равновесия сопровождается количественным, а в определенных случаях и качественным изменением деформаций в элементах системы. Эти формы потери устойчивости могут происходить одновременно или в отдельности в зависимости от типа сооружения и характера действующих на него нагрузок.

Ниже рассматривается потеря системой устойчивости формы равновесия в деформированном состоянии.

Возможность системы сохранять устойчивое положение в деформированном состоянии зависит от величины действующей на нее нагрузки. С увеличением нагрузки может наступать такое положение системы, которое становится неустойчивым состоянием равновесия. При наличии какого-либо сколь угодно малого возмущения происходит нарушение формы равновесия и система переходит в новое равновесное деформированное состояние.

Переход системы в качественно новое деформированное состояние принято называть потерей устойчивости ее равновесия или потерей устойчивости предыдущей формы деформаций. При этом деформации могут существенно возрастать при незначительном увеличении внешней нагрузки иди даже без ее увеличения. Рассматриваемый вид потери устойчивости обычно характеризуется деформациями системы, но это явление неразрывно связано с нарушением равновесия между внешними нагрузками и внутренними силами системы. Равновесие между внешними и внутренними силами упругой системы может быть устойчивым или неустойчивым. Граничное состояние системы между устойчивым и неустойчивым ее положением принято называть безразличным состоянием системы. Проследим это явление на примере центрально сжатого идеально упругого стержня (рис. 5.1,а). Если при некотором значении монотонно возрастающей нагрузки Р дать свободному концу стержня весьма малое отклонение от вертикального положения и убрать возмущающее воздействие, внешняя нагрузка будет стремиться удержать стержень в

71

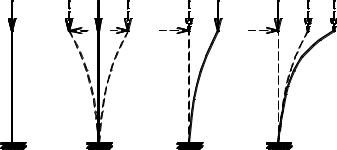
деформированном изогнутом состоянии, а внутренние силы – вернуть его в исходное прямолинейное положение.

Рис. 5.1

При устойчивом равновесии стержень, совершая колебания относительно вертикального своего положения, вернется в первоначальное состояние деформации центрального сжатия (рис. 5.1б). На рис. 5.1в показано безразличное состояние стержня, когда нагрузка возросла до PI > P . Под действием некоторого возмущения стержень перешел в новое равновесное деформированное состояние. При удалении постороннего возмущения форма равновесия стержня не изменяется. Упругие внутренние силы уже не способны вернуть стержень в исходное прямолинейное положение, а внешняя нагрузка еще не достигла такого значения при котором происходил бы дальнейший его изгиб. Дальнейшее увеличение нагрузки до некоторого значения PII > PI создает условие неустойчивого равновесия стержня. Любое сколь угодно малое возмущение или увеличение нагрузки вызовет переход стержня в новое состояние, характеризуемое интенсивным ростом деформаций изгиба и дальнейшим отклонением его от начального положения (рис. 5.1г). Таким образом, произойдет потеря устойчивости первоначальной формы равновесия центрально сжатого стержня.

Наибольшую нагрузку, при которой деформированная система еще находится в устойчивом положении, принято называть критической нагрузкой (Ркр ), а состояние системы под действием критической нагрузки – критиче-

ским ее состоянием.

72

При потере устойчивости переход системы в новое деформированное состояние происходит практически мгновенно с резким нарастанием деформаций и перераспределением усилий в элементах системы. В результате, как правило, конструкция переходит в аварийное состояние.

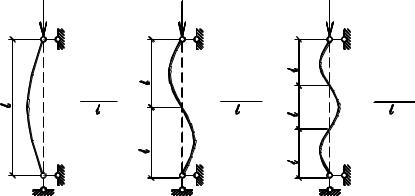
Существуют и высшие формы потери устойчивости, когда каждому значению критической нагрузки соответствует своя форма изогнутой оси сжимаемого элемента. Для одного и того же упругого стержня теоретически может быть найдено множество значений критических сил, каждой из которых соответствует своя форма изогнутой оси этого стержня. На рис. 5.2а-в показано, как с увеличением нагрузки изменяются формы потери устойчивости шарнирно опертой центрально сжатой стойки.

Рис. 5.2

Второй и третьей критическим силам (рис. 5.2б,в) соответствуют более сложные (высшие) формы изогнутой оси сжимаемой стойки, которые возможны теоретически, не являются устойчивыми и мгновенно переходят к простейшей форме деформации стержня (рис. 5.2а).

При решении практических задач отыскиваются значения критических нагрузок, которым соответствуют наиболее простые формы потери устойчивости.

Ниже рассмотрены наиболее часто используемые в расчетной практике методы определения критических сил в отдельных стойках и рамах при самой простой форме деформации сжимаемых элементов.

В зависимости от вида начальных деформаций и деформаций в момент

73

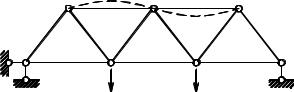
потери устойчивости различают (условно) потерю устойчивости первого и второго рода. Потеря устойчивости первого рода характерна тем, что в момент потери устойчивости появляются и сильно развиваются новые деформации. Эти новые деформации качественно отличаются от тех, которые возникают в начале загружения. Указанный вид потери устойчивости иначе называют потерей устойчивости по Эйлеру. К потере устойчивости первого рода относятся:

–потеря устойчивости центрального сжатия;

–потеря устойчивости плоской формы изгиба;

–потеря устойчивости симметричной формы деформации.

Приведем примеры потери устойчивости первого рода. Наиболее простым случаем этого явления может быть потеря устойчивости центральносжатой стойки (рис. 5.1). Если нагрузка меньше ее критического значения, стойка остается прямолинейной, находится в состоянии центрального сжатия, в ее сечениях возникают продольные деформации. Если нагрузка достигает своего значения равного Pкр , то прямолинейная форма равновесия стой-

ки становится неустойчивой и малейшее возмущение может вызвать переход стойки в новое деформированное состояние – криволинейное, которое будет для нее устойчивым. При этом возникают и интенсивно нарастают деформации нового вида – деформации изгиба.

На рис. 5.3 изображена ферма, элементы верхнего пояса которой при нагрузках P < Pкр будут испытывать деформации центрального сжатия.

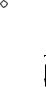PКР PКР

Рис. 5.3

При возрастании значений нагрузок, становится возможной потеря устойчивости первоначальной формы равновесия системы, элементы верхнего пояса могут выпучиться, их новая форма равновесия будет криволинейной с

74

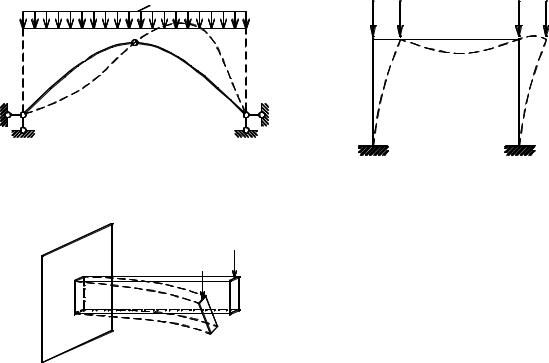
появлением и развитием деформаций изгиба.

В трехшарнирной арке параболического очертания под действием сплошной равномерно распределенной нагрузки, меньшей критической, все сечения будут испытывать деформации центрального сжатия (рис. 5.4). При увеличении нагрузки до qкр, состояние системы становится неустойчивым, и

любое малое возмущение может спровоцировать переход системы в новое деформированное состояние с появлением деформаций нового вида – деформаций изгиба.

Защемленная тонкая полоса при определенном значении внешней нагрузки отклонится от вертикального положения, произойдет дополнительный ее изгиб в горизонтальной плоскости и закручивание (рис. 5.6). До потери устойчивости балка испытывала только изгиб в вертикальной плоскости действия нагрузки. При потере устойчивости возникают и развиваются качественно новые деформации – деформации кручения.

При потере устойчивости второго рода деформации качественно остаются теми же, что и в начале загружения, но они интенсивно развиваются.

75

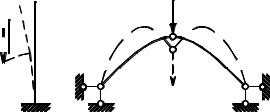
Примерами могут служить: внецентренно загруженная стойка (рис. 5.7а); трехшарнирная арка, на которую действует сосредоточенная нагрузка (рис. 5.7б). В обоих случаях, в начале загружения и в момент потери устойчивости, сечения элементов системы испытывают внецентренное сжатие, и деформации качественно не изменяются.

PКР

PКР

Рис. 5.7

В реальных конструкциях преобладает, как правило, потеря устойчивости второго рода ввиду неизбежного отклонения нагрузок от проектного положения (эксцентриситеты), неоднородности материала и др. В результате сжимаемые элементы стержневых систем еще до потери устойчивости испытывают внецентренное сжатие. Выход из строя такого типа элементов обычно происходит вследствие потери ими несущей способности (потери устойчивости второго рода) при нагрузках, численно меньших критических нагрузок первого рода. Тем не менее, при определении несущей способности сжа- то-изогнутых элементов сооружений необходимо знать их расчетные длины и гибкости, которые определяются с помощью критических сил первого рода. Поэтому изучение потери устойчивости первого рода имеет не только теоретическое, но и большое практическое значение.

Потеря устойчивости может происходить как в упругой, так и в упругопластической стадии работы материала конструкции. Ниже рассмотрены некоторые простые задачи потери устойчивости первого рода плоских упругих стержневых систем.

76

5.3.Число степеней свободы и формы равновесия

Впервой и второй частях курса строительной механики используется понятие «число степеней свободы системы», которое позволяет выявить пригодность системы в качестве инженерного сооружения и принадлежность ее

копределенному классу сооружений (W = 3 Д − 2Ш − Соп ). При этом полага-

ется, что все диски, составляющие систему, являются абсолютно жесткими и недеформируемыми.

В теории устойчивости рассматриваются системы в деформированном состоянии. Число степеней свободы характеризует (отражает) это состояние,

а именно: числом степеней свободы называют количество независимых геометрических параметров, определяющих положение всех точек системы в деформированном ее состоянии. Из этого следует, что число степеней свободы любой стержневой системы (балка, рама и т.д.) равно бесконечности. Количество возможных форм равновесия и соответствующих этим формам критических сил характеризуется числом степеней свободы системы. Реальная упругая система обладает бесконечным числом степеней свободы, бесконечным множеством форм равновесия и соответствующих этим формам критических нагрузок. В практических расчетах отыскивается наименьшее (не равное нулю) значение критической нагрузки. Этой нагрузке будет соответствовать наиболее простая форма деформации элементов системы.

С целью упрощения расчета упругая система может быть заменена более простой, имеющей конечное число степеней свободы, если это допускает заданная система, а также удовлетворяются требования к конечному результату. Это позволяет дифференциальные уравнения изгиба заменить алгебраическими и упростить решение задачи. Например, если в раме, изображенной на рис. 5.8а жесткость нагруженного стержня AB на изгиб (EI ) велика, а

жесткость стержня CD на изгиб (EI1 ) мала, то расчетную схему системы можно принять, как показано на рис. 5.8б. Пренебрегая изгибом нагруженной стойки AB, горизонтальные перемещения всех ее точек можно выразить через параметр dϕ, т.е. y(x)= x tg dϕ и мы получаем систему с одной степенью

77

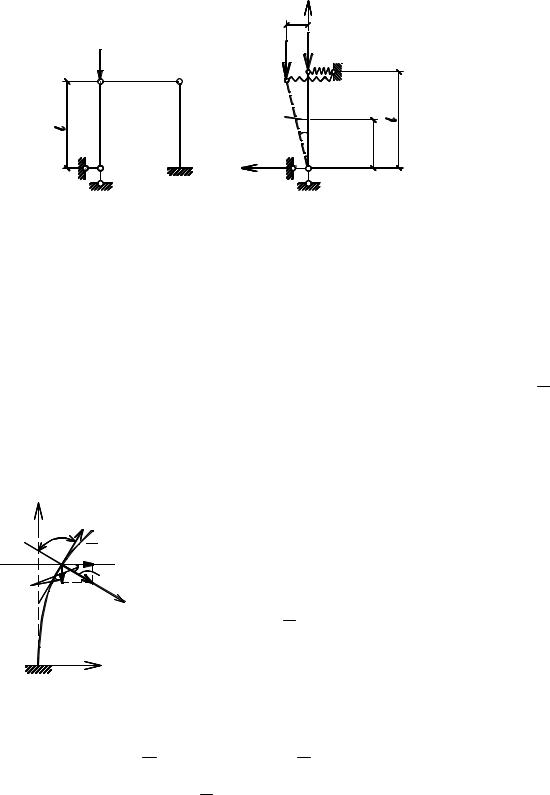
свободы. Величина Pкр будет зависеть от линейного перемещения упругой

опоры (конкретное решение такой задачи будет показано ниже).

Отметим, что с увеличением числа степеней свободы системы сложность решения задач устойчивости существенно возрастает.

Рис. 5.8

5.4. Уравнение устойчивости упругого сжато-изогнутого стержня

Рассмотрим некоторое поперечное сечение упругого сжато-изогнутого стержня, защемленного одним концом. Пусть от нагрузки, приложенной вы-

ше рассматриваемого сечения, будут вертикальная P и горизонтальная Q

составляющие (рис. 5.9). Определим поперечную силу в этом сечении из условия ∑n = 0.

Рис. 5.9

Ввиду малости перемещения dϕ имеем:

Q = Q cos dϕ + Ptgdϕ = Q 1+ Py′,

т.е. Q = Q + Py′ (а)

78

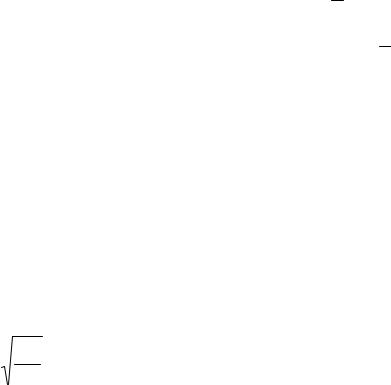
Как известно из сопротивления материалов

Подставляя последнее выражение в уравнение (а), получаем:

(− EIy′′)′ − Py′ = Q.

Дифференцируя еще раз по x , и учитывая, что Q′ = −q (где q – попе-

речная нагрузка на стержень), получаем окончательное уравнение равновесного состояния упругого сжато-изогнутого стержня:

определенных коэффициентов или другими приемами.

Для определения постоянных интегрирования C1, C2 , C3 и C4 исполь-

зуются граничные условия (нужно иметь четыре независимых друг от друга условия). Практическое использование граничных условий будет показано ниже при решении конкретных задач.

При отсутствии внешней поперечной нагрузки q уравнение (5.1) пре-

Решение уравнения (5.2) аналогично приведенному выше общему ре-

шению уравнения (5.1) с тем отличием, что отсутствует частное решение y0 .

79

При решении многих задач устойчивости отдельных стержней и стержневых систем (в случае малых деформаций в момент потери устойчивости) можно воспользоваться более простым дифференциальным уравнением второго порядка: ± EIy′′ = M x , применение которого будет показано также ниже на конкретных примерах.

5.5.Методы решения задач устойчивости

Решения задач устойчивости может выполняться точными (с учетом принимаемых допущений), или же приближенными методами. Ниже мы рассмотрим те методы, которые наиболее часто используются в расчетной практике.

Статический метод. При использовании этого точного метода упругую систему рассматривают в таком деформированном состоянии, которое отличается от заданного бесконечно малыми перемещениями, обеспечивающими появление деформаций нового вида, качественно отличающихся от начальных. Для элементов системы в деформированном состоянии составляют дифференциальные уравнения равновесия и путем их интегрирования отыскивают решение. Используя граничные условия, формируют систему однородных линейных уравнений, количество которых равно числу неизвестных постоянных после интегрирования уравнений равновесия. Новое деформированное состояние системы будет иметь место, если все постоянные в системеоднородных линейных уравнений одновременно не равны нулю. В этом случае определитель, составленный из коэффициентов при постоянных, должен быть равным нулю, т.е.

D(n)= 0 . (5.3)

Равенство (5.3) называется характеристическим уравнением (уравнением устойчивости), решая которое, находят критические силы или же критические параметры, через которые затем отыскивают критические силы.

Применение статического метода рассмотрим на примере упругого центрально сжатого стержня постоянного сечения (рис. 5.10).

80