Строительная механика

Как и в предыдущем случае, уравнение (5.36) решается подбором такого значения nl , при котором удовлетворяется равенство, а затем по формуле (5.34) находят значение критической силы.

Установим предельные значения nl и Pкр для решаемой задачи.

1)При C = 0, tg(nl)= 0 и значения ( nl ) могут быть:

nl = 0 ; nl =π ; nl = 2π и т.д.

В рассматриваемом случае все значения nl > 0 не могут быть реализованы, так как значение C = 0 соответствует наличию шарнира в упруго защемленной опоре и заданная система становится геометрически

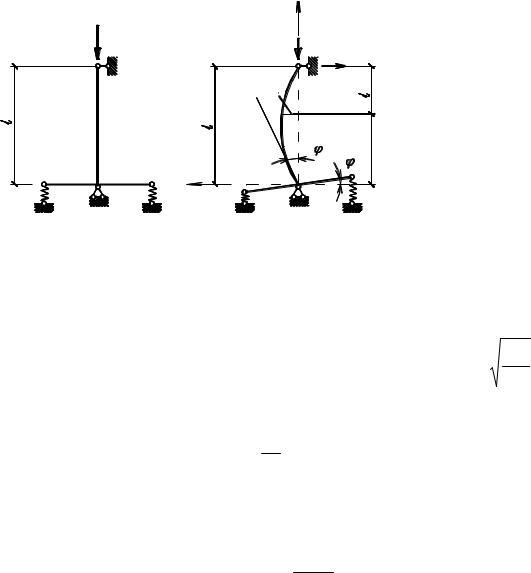
На рис. 5.20а приведен пример центрально нагруженной стойки, верхняя шарнирная опора которой не может смещаться по горизонтали, а нижняя опора – упруго защемленная. Решение этой задачи статическим методом с использованием зависимости − EIy′′ = M x аналогично предыдущему (рис 5.20,б):

Mx = Pкрy +R(l −x).

101

имеем:

y′′ + n2 y = − EIR (l − x).

Решение этого неоднородного дифференциального уравнения имеет

вид:

y = A sin(nx)+ B cos (nx)− n2REI (l − x).

102

(стойка с верхним шарнирно опертым и нижним защемленным концами).

103

5.8. Устойчивость плоских рам

Общие положения

Рассмотренные выше (5.5) методы решения задач устойчивости являются общими и используются для определения критических сил как в отдельных стержнях, так и в любых стержневых системах, в том числе в рамах. Основными являются статический и энергетический методы. Ниже рассматривается применение статического метода в расчетах на устойчивость рам.

С целью упрощения расчета рам на устойчивость принимаются следующие допущения:

–рассматривается только узловая нагрузка, не вызывающая поперечного изгиба стержней рамы;

–предполагается, что критическое состояние рамы достигается при одновременном и пропорциональном возрастании всех узловых нагрузок;

–стержни рамы принимаются несжимаемыми и нерастягиваемыми (пренебрегают изменениями длин стержней, вызванными продольными деформациями в этих стержнях);

–пренебрегают сближением концов стержня при его изгибе;

–не учитываются изменения продольных и поперечных сил в стержнях при их изгибе в момент потери устойчивости.

Первое допущение: узловая нагрузка принимается на том основании, что рассматривается потеря устойчивости первого рода, а остальные – ввиду малости деформаций в момент потери устойчивости при бесконечно малых перемещениях заданной системы.

Такой подход в исследовании устойчивости рам применяется при действии на них любых (в том числе внеузловых) нагрузок. Для определения узловых нагрузок выполняется расчет системы на прочность. Найденные значения продольных сил в элементах системы играют роль узловых нагрузок в расчете ее на устойчивость.

На рис. 5.21а приведена рама, в которой сосредоточенная нагрузка

104

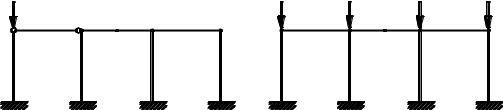
приложена только в одном узле. Критическую нагрузку можно было бы нахо-

Рис. 5.21

дить для нагруженной стойки с упругой опорой. Но этот прием в данном случае неэффективен. Критическая сила зависит от линейного смещения этой упругой опоры. Определение характеристики упругой опоры окажется более громоздким, чем исследование устойчивости системы в целом. Кроме того, в реальных конструкциях нагрузки будут приложены во всех узлах рамы и условия задачи требуют исследования устойчивости системы с нагруженными (сжимаемыми) элементами.

Расчет на устойчивость рам чаще всего выполняется методом сил или методом перемещений. Выбор рационального метода зависит от конкретной системы и диктуется количеством основных неизвестных. В расчетной практике чаще используется метод перемещений.

Метод перемещений. Ход расчета на устойчивость методом перемещений тот же, что и при расчете на прочность.

Устанавливается степень кинематической неопределимости системы и принимается основная система путем введения дополнительных связей, препятствующих возможным угловым и линейным смещениям узлов заданной системы. Содержание этого этапа расчета остается обычным.

Формируется система канонических уравнений, построение которых и их физический смысл остаются обычными. Отличие будет в том, что основные неизвестные Zi – малые перемещения, возникающие в момент потери устойчивости. Так как на раму действует узловая центрально приложенная нагрузка, то в нагруженных элементах возникают только продольные усилия и реакции в дополнительно введенных связях от внешней нагрузки ( Ri p ) до

105

момента потери устойчивости равны нулю. Канонические уравнения метода перемещений превращаются в однородные линейные уравнения вида:

Коэффициенты при неизвестных уравнений (5.38) выражают реакции в дополнительно введенных связях, возникающие в основной системе при поочередном перемещении узлов системы на единицу по направлениям воз-

можных смещений этих связей. В расчетах на прочность коэффициенты ri k

при неизвестных Zi в обычных уравнениях метода перемещений не зависят от внешних нагрузок. В системе же уравнений (5.38) эти коэффициенты определяются с учетом продольных сил в стержнях, зависящих от внешних узловых нагрузок. В этом заключается основная особенность использования классических методов (например, метода сил и метода перемещений) в расчетах на устойчивость. Для коэффициентов системы уравнений (5.38) остает-

ся справедливой теорема о взаимности реакций ri k = rk i .

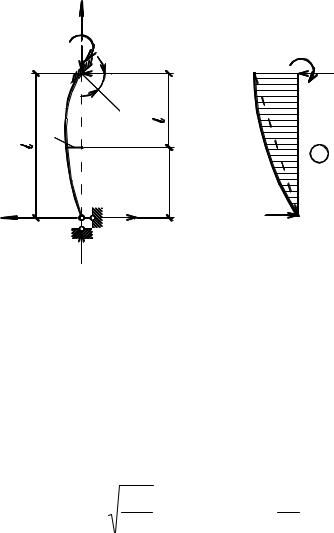
Реакции в дополнительно введенных связях основной системы с учетом продольных сил в сжатых стержнях от единичных угловых и линейных смещений могут быть получены различными способами. Рассмотрим стержень постоянного сечения с одним защемленным и вторым шарнирным концами в деформированном состоянии и определим опорный момент в защемлении и поперечные силы на концах стержня при повороте защемляющей опоры на угол равный единице. Для решения задачи воспользуемся статическим методом и дифференциальным уравнением изгиба (5.4)

−EI y′′ = M x .

Всилу принятых допущений из условия равновесия системы верти-

кальная реакция VA может быть принята равной критической силе (VA = Pкр ),

а горизонтальные реакции на концах стержня – поперечным силам

106

(H A = H B = Q).

Для определения постоянных A и B воспользуемся граничными усло-

107

108

зи при повороте ее на угол равный единице без учета продольного изгиба сжимаемого стержня. Они известны из расчета рам методом перемещений на прочность. Влияние продольной силы на величину поперечной силы (Q) и

изгибающего момента (M ) учитывается функцией ϕ1(ν ) (5.46). Общий вид эпюры изгибающего момента и поперечные силы в рассмотренном случае с учетом продольного изгиба стержня показаны на рис. 5.22б.

Выполняя аналогичные операции, получим выражения поправочных множителей для учета влияния продольного изгиба в стержнях с другими опорными закреплениями при различных единичных смещениях узлов.

Единичные эпюры изгибающих моментов для ненагруженных продольными силами стержней строятся с использованием таблицы метода перемещений, применяемой в расчетах на прочность (табл. 4.1). Эпюры изгибающих моментов в нагруженных стержнях имеют криволинейное очертание. Влияние сжимающих сил учитывается (как показано выше) введением поправочных множителей.

В таблице 5.2 показаны эпюры изгибающих моментов, значения этих моментов и поперечных сил на концах сжатых стержней с различными опорными закреплениями при единичных угловых и линейных перемещениях опор этих стержней. Там же приведены выражения поправочных множителей, учитывающих продольный изгиб сжатого стержня.

Числовые значения функций типа ϕi (ν ) и ηi (ν ) приведены в таблице

109

5.3, которые используются при решении конкретных задач. Система однородных уравнений (5.38) допускает следующие решения. Если принять все перемещения Z1, Z2 , ..., Zn одновременно равными нулю, то уравнения (5.38)

будут тождественно удовлетворяться, но это условие соответствует недеформированному состоянию стержневой системы, отсутствует изгиб ее стержней. Поскольку при решении задач устойчивости рассматривается деформированное состояние системы, отличное от начального ее состояния, то все Zi не могут быть одновременно равными нулю и уравнение (5.38) будет удовлетворяться при условии, когда определитель из коэффициентов при неизвестных равен нулю, т.е.:

Раскрывая определитель (5.48), получаем уравнение устойчивости метода перемещений в развернутом виде (характеристическое уравнение). По наименьшему значению положительного корня характеристического уравнения, пользуясь условием (5.40), находим критическую нагрузку. В общем случае после раскрытия определителя (5.48) получаем одно уравнение с несколькими неизвестными νi для загруженных стержней. Решаются такие уравнения путем пробных попыток. С целью упрощения расчета целесообразно все νi , фигурирующие в расчете, выразить через один параметр ν и

упростить исходное уравнение. Прежде чем задаваться каким-либо конкретным значением ν при решении уравнения устойчивости, полезно установить нижнюю и верхнюю пределы (условные) этого параметра. Выполнение этих процедур будет показано ниже на конкретном примере.

110