
Строительная механика
.pdf
Проверим правильность вычисления свободных членов уравнений (а)
EI ∑∫ |
|
P |
|
S dx |
|
8 |
|
1 |
10 +15 |
|
|
|
|
M |
M |
= − |
(112 8 + 4 4 40 + 0)− |
4 |
112 |
= |
|||||||
6 8 |
1 |
2 |
|||||||||||
|
|
EI |
|
|
|
|
|
||||||
= −256 −5600 = −5856.
EI (∆1P + ∆2P + ∆3P ) = (−1792)+ (− 3840)+ (− 224)= −5856.
Следовательно, перемещения δ и ∆ в уравнениях (а) определены правильно.
Подставив значения вычисленных перемещений в исходные уравнения
(а), имеем:
72 X 1 +
128 X 1 +
28 X 1 +3
128 X 2 |
+ |
28 |
X 3 |
− |
1792 = |
0; |
|||||
3 |
|||||||||||
832 |
|
|
|
|
|
|
|
||||
X |
2 |
+ |
16 X 3 |
− |
3840 = |
0; |
|||||
3 |
|||||||||||
|
|
|
|
8 |
|
|
|
|
|
||
16 X 2 |
|
+ |
|
X 3 |
− |
224 = |
0, |
||||
|
|
|
|||||||||
|
|
|
|
3 |
|
|
|
|
|||
откуда |
X1 =1,57665кН , X 2 =13,1387 кН , X 3 = −0,350366 кНм. |
Проверка правильности решения системы уравнений производится путем подстановки полученных значений Xi в исходные уравнения, например:
первое уравнение
72 1,57665 +128 13,1387 + 283 (− 0,350366)−1792 =
=113,519 +1681,75 − 3,27008 −1792 = −1795,27 +1795,27 = 0 и т.д.
Аналогично должны быть выполнены подстановки Xi во все осталь-
ные исходные уравнения.
Окончательная эпюра изгибающих моментов может быть получена по условию (3.4), т.е. M = M р + M 1 X1 + M 2 X 2 + M 3 X3 .
Эпюры изгибающих моментов от фактических значений X1, X 2 и X3
приведены на рис. 3.7, а результирующая эпюра – на рис. 3.8.
41
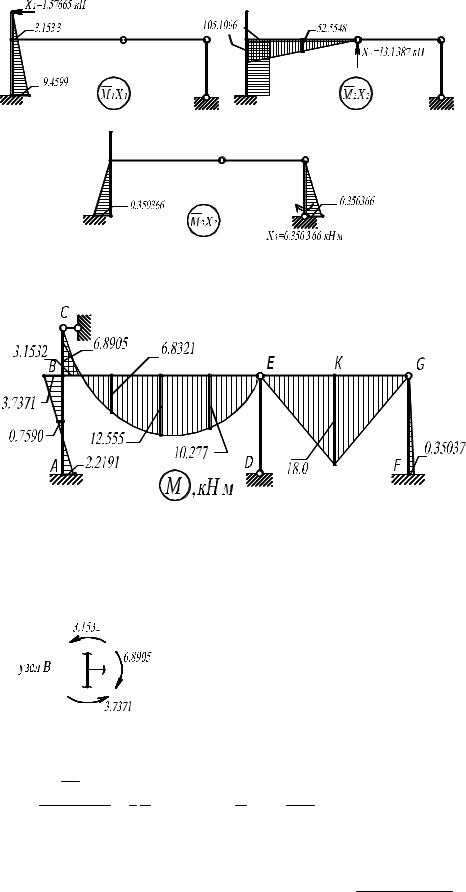
Рис. 3.7
Рис. 3.8
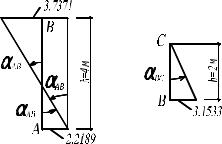
Проверки правильности окончательной эпюры изгибающих моментов: 


 статическая проверка (см. рис. 3.9):
статическая проверка (см. рис. 3.9):
|
|
|
∑M узла"B" = 6,8905 −3,1532 −3,7371 |
|
|||
|
|
|
= 6,8905 − 6,8903 = 0; |
|
|
||
Рис. 3.9 |
|
кинематические проверки выполня- |
|||||
|
ются по условию (3.5): |
|
|
||||
|
|
|
|
|
|||
EI ∑∫ M M 1 dx |
= 1 1 3,1533 2 |
2 |
2 + 4 |
1 |
× |
|
|
EI |
1 2 |
3 |
6 |
|
|
|
|
×(− 3,7371 2 − 4 0,7590 4 + 6 2,2191)= 4,2044 − 4,2024 = 0,002; |
|||||||
относительная погрешность вычислений µ= 0,002 100% |
= 0,05% |
; |
|||||
|
|
|
|
|
4,2024 |
|
|
42
EI ∑∫ M |
M |
|
2 dx |
= |
|
8 |
|
|
(− 6,8904 8 + 4 12,5548 4 + 0)− |
|||
EI |
6 |
8 |
||||||||||
|
|
|
|
|
|
|||||||
− |
18 4 0,7590 = 24,2923 − 24,2880 = 0,0043, µ = 0,02%; |
|||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
EI ∑∫ M |
|
3 dx |
|
|
4 |
|
|
|
|
|||
M |
= |
|
|
|
(3,7371 0 |
− 4 0,7590 0,5 + 2,2191 1)− |
||||||
EI |
|
6 1 |
||||||||||
|
|
|
|
|
|
|||||||
− |
1 1 0,35037 4 2 |
1 = 0,4674 |
− 0,46716 = 0,00024, µ = 0,05%. |
|||||||||
|
1 2 |
|
|
|
|
|
3 |
|
|
|
|
|
Статическая и кинематические проверки выполняются и, следовательно, окончательная эпюра изгибающих моментов построена верно.
Для построения эпюры поперечных сил воспользуемся окончательной эпюрой изгибающих моментов (M ).
На участках, где эпюра M имеет прямолинейное очертание, поперечная сила численно равна
Q = dMdx = ±tgα,
где α – угол наклона эпюры M к оси стержня. Если для совмещения с эпюрой изгибающих моментов стержень нужно поворачивать по ходу часовой стрелки, то поперечная сила принимается положительной. Например, на участке АВ (рис. 3.10) имеем
Q |
|
= tgα |
|
|
3,7371 + |
2,2191 |
= −1,48905кН. |
AB |
AB |
= − |
4 |
|
|||
|
|
|
|
|
Аналогично получаем значения поперечных сил на участках BC, GR,
EК и KG:
|
|
|
|
|
|
QBC = − |
3,1532 |
= −1,5766кН; |
|||
|
|
|
|
|
|
|
|
|
2 |
|
|
Рис. 3.10 |
|
|
|
|
|
QGF = − |
0,35037 |
= −0,0876кН; |
|||
|
|
|
|
|
|
|
|
|
4 |
|
|
Q = + |
18 |
|
= +6кН; |
Q |
|
= − |
18 |
= −6кН . |
|
|
|
|
|
KG |
|
|
|
||||||
EK |
3 |
|
|
|
3 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
43
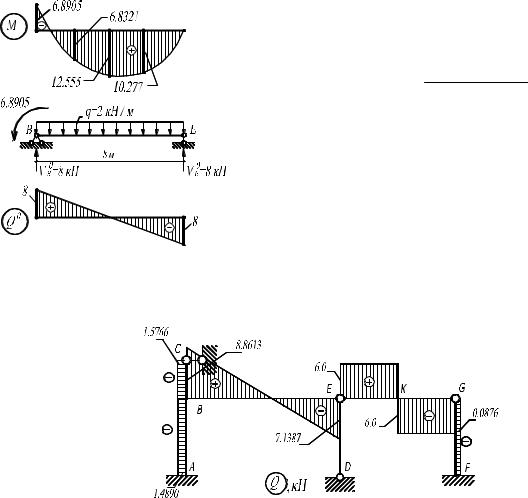
Отдельные элементы системы с действующими на них внешними нагрузками можно рассматривать как однопролетные шарнирно опертые балки в эквивалентном состоянии. При этом должны быть учтены опорные моменты (если таковые имеются) с учетом их знаков. Найденные значения суммарных опорных реакций на концах элемента будут равны соответствующим поперечным силам. Поперечные силы таких элементов могут быть так же найдены по формуле (3.6).
Например, на участке BE, где эпюра M – криволинейна (рис 3.11), значения поперечной силы по формуле (3.6) имеем:
Qx = Qx0 + |
M пр − Млев |
; |
|
||
|
l |
|
= (+ )+ 0 − (− 6,8904)= QB 8 8
= (+ 8)+ 0,86130 =8,8613кН;
QE = (−8)+ 0,86130 = −7,1387к,1
Рис. 3.11
Окончательная эпюра поперечных сил приведена на рис. 3.12.
Рис. 3.12
Эпюру продольных сил (N ) построим по эпюре поперечных сил Q ,
рассматривая равновесие узлов. Узлы рамы вырезаем в такой последовательности, чтобы каждый рассматриваемый узел содержал не более двух стержней с неизвестными продольными силами. При составлении уравнений рав-
44
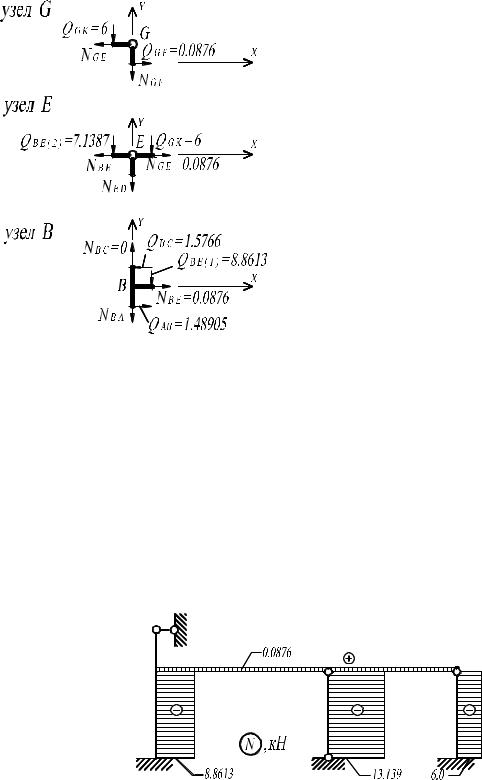
новесия (например, ∑ X = 0 , ∑Y = 0 ) вначале полагается, что все неиз- |
|
вестные продольные силы являются растягивающими |
(положительными). |
Отсеченные узлы рассматриваемой рамы приведены на |
рис. 3.13. |
Узел G:
∑ X = 0; N GE −0,0876 =0;
NGE = 0,0876кН
(стержень GE растянут).
∑Y = 0; − NGF − 6,0 = 0; NGF = −6,0кН
(стержень GF сжат). Узел Е:
∑X = 0; 0,0876 − NBE = 0; NBE = 0,0876кН .
∑Y = 0 ; N ED + 6 + 7,1387 = 0 ;
Рис. 3.13 |
NED = −13,1387кН . |
|
Узел В:
∑X = 0; 0,0876 −1,5766 +1,4890 = −1,5766 +1,5766 = 0 ;
∑Y = 0 ; NBA + 8,8613 = 0;
NBA = −8,8613кН .
Окончательная эпюра продольных сил (N ) приведена на рис. 3.14.
Рис. 3.14
45

Проверим равновесие системы в целом. По эпюрам Q , N и Ì из усло-
вий равновесия опорных узлов получены опорные реакции (рис. 3.15).
Рис. 3.15
По формулам (3.7) имеем:
∑X = 0; 1,4890 −1,5766 + 0,0876 =1,5766 −1,5766 = 0;
∑Y = 0; 8,8613+13,1397 +6 −2 8 −12 = 28 −28 = 0 ;
∑M A = 0; −1,5766 6 + 2 8 4 +12 11+ 0,35037 + 2,2191−
−13,139 8 − 6 14 = +198,57 −198,57 = 0 .
46
Глава 4
Расчет стержневых систем методом перемещений
4.1. Общие положения
Метод перемещений (деформаций), широко применяется в расчетах сложных рамных каркасов, ферм с жесткими узлами и многих других статически неопределимых стержневых систем. Он оказался эффективным методом для решения задач устойчивости и динамики сооружений, явился хорошей основой для разработки многих приближенных способов расчета рам и других стержневых систем.
В методе сил основными неизвестными являются усилия в избыточных связях и для отыскания этих усилий используются кинематические уравнения, выражающие условие отсутствия перемещения по направлению отбрасываемых связей. В методе перемещений за основные неизвестные принимаются угловые и линейные перемещения узлов, и отыскивают эти перемещения с помощью уравнений равновесия.
Мы рассмотрим применение метода перемещений в расчетах плоских статически неопределимых рам. Приведенные сведения могут быть использованы в расчетах этим методом и других стержневых систем.
4.2. Кинематическая неопределимость упругой стержневой системы
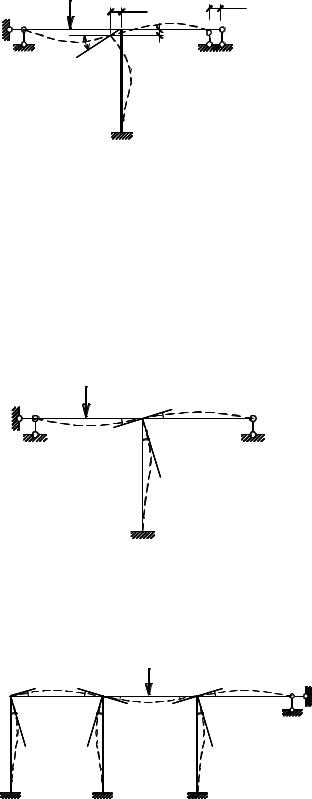
Под действием нагрузок элементы системы, выполненной из реальных материалов, будут деформироваться и происходят перемещения ее узлов. Количество возможных перемещений узлов системы служит показателем сложности расчета методом перемещений. Чем большим количеством перемещений узлов обладает система, тем более трудоемок ее расчет.На рис. 4.1 изображена рама под действием нагрузки P . Ввиду деформаций ее элементов жесткий узел 1 повернется на некоторый угол (Z1 ), переместится по го-
ризонтали (Z2 ) и по вертикали (Z3 ). Таким образом, каждый жесткий вне-
47
опорный узел системы в общем случае обладает тремя возможными переме- |
|||
щениями. |
|
|
|
P |
Z2 |
Z2 С целью упрощения расчета в методе пе- |
|
1 |
|
ремещений принимаются следующие ос- |
|
|
3 |
||
Z1 |
Z |
|
|
|
новные допущения: 1) В системах, эле- |
||
|
|
||
|
|
менты которых работают преимущест- |
|
|
|
венно на изгиб, пренебрегают перемеще- |
|
Рис. 4.1 |
ниями узлов, вызванными продольными |
||
деформациями стержней, ввиду малости |
|||
|
|
||
|
|
этих перемещений в сравнении с переме- |
|
щениями от изгиба этих стержней. |
|||
2) Пренебрегают сближением концов стержней при их изгибе, т. е. дли- |
|||
ны стержней принимаются постоянными, численно равными своим значени- |
|||
ям в начальном недеформированном состоянии. |
|||
P |
Z1 |
Если учесть принятые допущения, то |
|
|
в раме, приведенной на рис. 4.1 сле- |
||
Z1 |
|
||
Z1 |
дует принять Z2 = 0 , Z3 = 0 и узел 1 |
||
|
|
||
|
|
будет обладать одним перемещением |
|
|
|
– углом поворота Z1 (рис. 4.2). При |
|
Рис. 4.2 |
этом все стержни, примыкающие к |
||
|
|||
узлу 1, повернутся на один и тот же угол Z1, так как должно обеспечиваться |
|||
условие неразрывности деформаций. |
|||
Z1 |
Z2 2 Z2 |
P |
Z3 |
С |
учетом принятых допу- |
Z3 3 |
щений, |
установим подвижность |
|||
1 |
|
|
Z3 |
||
Z1 |
Z2 |
|
узлов рамы, изображенной на рис. |
||
|
|
|
|
||
|
|
|
|
4.3. Вертикальными и горизон- |
|
|
|
|
|
тальными смещениями узлов 1, 2 и |
|
|
Рис. 4.3 |
|
3, вызванными продольными де- |
||
|
|
формациями |
|||
|
|
|
|
||
48
стержней и сближением концов этих стержней при изгибе пренебрегаем. Нагрузка P вызовет изгиб ригеля в пролете 2-3. Жесткие узлы 2 и 3
повернутся на некоторые углы, произойдет изгиб остальных стержней системы и поворот узла 1, как показано на рис 4.3. При этом в каждом узле все стержни повернуться на один и тот же угол (Z1, Z2 и Z3 ). Таким образом, под действием внешней нагрузки все жесткие внеопорные узлы системы могут иметь угловые перемещения, количество которых обозначим через ny . В на-
шем случае ny = 3.
При изгибе стержней узлы системы (жесткие и шарнирные) могут перемещаться линейно. В рассмотренном примере (рис. 4.3) можно принять, что перемещения ригеля рамы и ее внеопорных узлов 1, 2 и 3 в горизонтальном направлении отсутствуют, так как этому препятствует горизонтальный опорный стержень на крайней правой опоре, а взаимными перемещениями узлов пренебрегаем в силу принятого допущения. Перемещением этих узлов по вертикали пренебрегаем на основании принятого допущения о малости перемещений, обусловленных продольными деформациями.
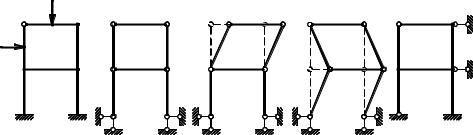
Рассмотрим раму, изображенную на рис. 4.4а.
а) |
P2 |
б) |
в) |
|
2 |
4 г) 2 |
4 |
д) |
|
1 |
4 |
|
|
||||||||
2 |
1 |
1 |
|
|
|
|
|
|
|
|
P1 |
|
|
|
|
|
|
|
|
|
|
1 |
3 |
2 |
2 |
1 |
3 |
1 |
|
3 |
|
2 |
А |
В |
А |
В |
А |
В |
А |
В |
|
А |
В |
Рис. 4.4
Количество угловых перемещений равно числу жестких узлов, т.е. ny = 3. Перемещениями узлов по вертикали и их взаимным сближением пре-
небрегаем по принятым выше допущениям. По горизонтали рама в целом может перемещаться, так как при изгибе стоек сместятся ее узлы. При этом узлы одного этажа переместятся по горизонтали на одну и ту же величину. Для определения линейных перемещений узлов рамы можно воспользоваться ее шарнирной схемой, получаемой путем введения шарниров в жесткие про-
49
межуточные узлы и опорные защемления заданной системы. Число степеней свободы полученного механизма равно числу возможных линейных перемещений узлов системы. В нашем случае шарнирная схема рамы показана на рис. 4.4б и число линейных перемещений узлов пл = 3 Д − 2Ш − Соn = 3 6 − 2 6 − 4 = 2 (на рис. 4.4б цифрами 1, 2 обозначена кратность шарниров). Найденное выше число линейных перемещений узлов системы является количественным показателем. Направления этих перемещений узлов выявляются путем анализа изменения структуры шарнирной схемы системы. Например, в нашем случае в горизонтальном направлении могут сместиться на одну и туже величину узлы 2 и 4 независимо от остальной части рамы (рис. 4.4в), или же узлы 1, 3 независимо от узлов 2 и 4 (рис. 4.4г). Чтобы воспрепятствовать этим линейным перемещениям, в заданной системе следует поставить две связи (рис. 4.4д).
Таким образом, общее число возможных угловых и линейных перемещений узлов рассматриваемой рамы будет:
n = ny + nл = 3 + 2 = 5.
Количество независимых угловых и линейных перемещений всех узлов системы называют степенью ее кинематической неопределимости.
4.3. Сущность метода перемещений. Канонические уравнения
Метод перемещений основан на том, что в качестве основных неизвестных принимаются угловые и линейные перемещения узлов системы. Зная эти перемещения, можно определить усилия в элементах системы.
Последовательность расчета методом перемещений остается по существу такой же, как и в методе сил. Расчет методом перемещений выполняется также с использованием вспомогательной системы, называемой основной системой (О.С.). Основную систему принимают путем введения дополнительных связей, препятствующих всем возможным угловым (защемляющие связи) и линейным (отдельные стержни) перемещениям узлов системы. При
50
