
DIF_calc_2013
.pdf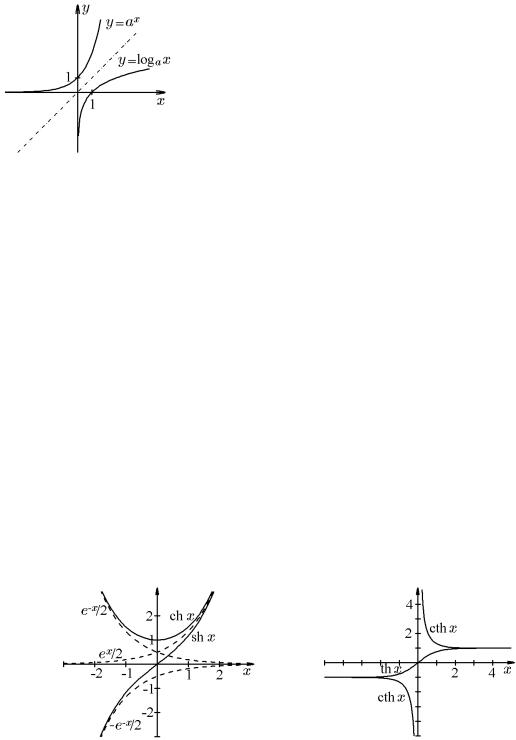
180 |
Глава 3. Теория пределов |
IV. Показательная функция |
|
Показательная функция y = ax при a > 1 непре-
рывна и монотонно возрастает на R (рис. 50). Это вытекает из следствия 9.13.1:
lim ax = ax0
и пределов |
x→x0 |
|
|
|
|
|
|
|
|
|
|
|
|
x lim |
ax = 0, |
x |
lim ax |
= +∞ |
. |
|
|
+ |
∞ |
|
|||
→−∞ |
|
|
→ |
|
|
|
Этот Рисже .результат50. можно получить из асимптотической оценки при x → 0: y = ax0+Δx − ax0 = ax0 (a x − 1) = ax0 ln a x + o(Δx),
поскольку
lim [ax0 ln a x + o(Δx)] = 0.
x→x0
Очевидно, что при a < 1 показательная функция y = ax непрерывна и монотонно убывает на R.
V. Гиперболические функции
Их непрерывность, согласно теореме 9.9, непосредственно вытекает из непрерывности показательной функции, поскольку все они рационально выражаются через ex (рис. 51):
sh x = |
1 |
(ex − e−x), |
ch x = |
1 |
(ex + e−x); |
|||||
|
|
|
|
|||||||
2 |
2 |
|||||||||
|
th x = |
sh x |
, |
cth x = |
|
|
1 |
. |
||
|
ch x |
|
|
|
||||||
|
|
|
|
|
|
|
th x |
|||
Из определения гиперболических функций следует, что ряд их свойств «аналогичен» свойствам тригонометрических, например
sh(x + y) = sh x ch y + ch x sh y, ch(x + y) = ch x ch y + sh x sh y, ch2 x − sh2 x = 1,
и т.д.
Рис. 51.
♦ Само название «гиперболические» объясняется тем, что уравнения x = a ch t, y = b sh t можно рассматривать как параметрические уравнения (см. [11]) гиперболы x2/a2 − y2/b2 = 1, тогда как уравнения x = a cos t, y = b sin t которые задают эллипс x2/a2 + y2/b2 = 1.



12. Непрерывность функции одного аргумента |
183 |
Решение. Поскольку все значения аргумента, при которых следует вычислить пределы, принадлежат областям определения этих функций, то соответствующие пределы равны значениям функций в этих точках.
Пример 12.16. Показать справедливость представления показательной функ-
ции
ex = lim 1 + x n.
n→∞ n
Решение. Исходное выражение под знаком предела при x = 0 можно представить в виде
1 + n |
|
|
= |
1 + n |
|
. |
||
|
x |
|
n |
|
|
x |
n/x |
x |
Так как при n → ∞ x/n → 0, то выражение в квадратных скобках стремится к e, но тогда в силу непрерывности степенной функции (при фиксированном x) все выражение имеет своим пределом ex.
Пример 12.17. Вычислить предел
A = lim x4/(4+ln x). x→0
Решение. Имеем неопредел¨енность вида (00). Логарифмическая функция непрерывна, поэтому неопредел¨енность можно привести к виду (0 · ∞). Действительно,
ln |
|
= |
x→0 |
x→0 |
x→0 |
4 + ln x ln |
|
ln x |
· ∞ |
|
|
|
|||
|
A |
|
ln[lim x4/(4+ln x)] = lim ln[x4/(4+ln x)] = lim |
4 |
|
|
x = (0 |
|
|
) = |
|||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
lim |
|
|
= 4 |
· |
1 = 4, |
|||
|
|
|
|
|
|
|
4 + ln x |
||||||||
|
|
|
|
|
|
= 4 x→0 |
|
|
|
||||||
откуда A = e4.
Пример 12.18. Вычислить пределы из примера 10.13.
Решение. Функция y = ln x непрерывна, поэтому предел
1) 1 = x→∞ sin x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
|
|
1 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
A |
lim |
|
|
+ cos |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
можно записать в виде |
|
|
|
|
|
|
x |
x→∞ |
x |
x |
x |
|
|
|
|||||||||||
ln 1 |
= x→∞ |
|
|
|
x |
|
|
|
|
|
|||||||||||||||
A |
lim |
x ln |
sin |
1 |
+ cos |
1 |
|
= lim |
x ln |
1 |
+ o |
1 |
|
+ 1 + o |
1 |
= |
|
||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
|
1 + 1/x |
= 1, |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1/x |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→∞ |
|
|
|
||
т.е. A1 |
= e. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично вместо предела |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2) A2 = lim(4 |
− |
2x |
− |
x2) |
(x−1)3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x→1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

184 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Глава 3. Теория пределов |
|||||||||||||||
вычислим предел |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ln A |
= lim |
ln(4 − 2x − x2) |
= lim |
ln[1 − (x + 3)(x − 1)] |
= |
lim |
(x + 3)(x − 1) |
= |
||||||||||||||||||||||||||||||
2 |
x |
→ |
1 |
(x |
− |
1)3 |
|
x |
→ |
1 |
|
|
(x |
− |
1)3 |
|
|
|
− x |
→ |
1 |
|
|
|
(x |
− |
1)3 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
4 lim |
x − 1 |
= |
−∞ |
, |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− x |
→ |
1 |
(x |
− |
1)3 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
т.е. A2 |
= e−∞ = 0. Здесь мы воспользовались соотношением ln(1 + z) z, z → 0. |
|||||||||||||||||||||||||||||||||||||
Вместо предела |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3 = x→2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3) A |
lim |
|
1 + sin |
|
πx |
|
ctg(πx/2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
удобно вычислить предел |
1 + sin 2 |
|
|
− x→2 |
|
|
|
|
|
|
|
|
|
|
|
= −1 |
|
|
|
|||||||||||||||||||
|
ln |
|
3 = x→2 |
|
|
|
|
2 ln |
|
sin(πx/2) |
|
|
|
|
|
|
||||||||||||||||||||||
|
A |
|
|
lim |
ctg |
πx |
|
|
|
|
|
πx |
= |
|
lim |
ln[1 + sin(πx/2)] |
|
|
|
|
|
, |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
т.е. A3 = e−1.
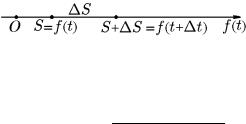
ГЛАВА 4
Дифференциальное исчисление
13.Производная и дифференциал функции одной переменной
13.1.Задачи, приводящие к понятию производной. Определение производной, е¨ геометрическое и механическое толкования
Известно, что методы элементарной математики не применимы к решению ряда задач. Так, можно вычислить среднюю скорость неравномерного движения в заданный промежуток времени, но невозможно методами элементарной математики найти мгновенную скорость в произвольный момент времени.
Изучение производной, или скорости изменения функции (правила дифференцирования, свойства производной), и составляет предмет дифференциального исчисления.
Рассмотрим задачи из физики и геометрии, приводящие к понятию производной, а затем дадим определение производной и выясним е¨ механический и геометрический смысл.
Мгновенная скорость неравномерного прямолинейного движения
Пусть материальная точка движется по прямой из начального положения O (рис. 53) и за время t проходит путь S. Очевидно, что пройденный путь S есть функция времени:
S = f(t). |
(13.1) |
К моменту времени t + t материальная точка пройд¨ет путь |
|
S + S = f(t + t), |
(13.2) |
а за время t: |
(13.3) |
S = f(t + t) − f(t). |
Рис. 53.
При равномерном движении точки е¨ скорость за промежуток времени t постоянна и равна средней скорости
vср = |
S |
= |
f(t + t) − f(t) |
. |
t |
|
|||
|
|
t |
||
Если же точка движется неравномерно, то средняя скорость не совпадает со скоростью в данный момент времени t.
С уменьшением промежутка времени t отклонение vcp = S/ t от скорости в момент t уменьшается. Истинная скорость движения точки в момент t определяется как предел
lim v |
cp |
= lim |
S |
= v(t). |
|
t |
|||||
t→0 |
t→0 |
|
Этот предел, если он существует, называется скоростью движения в данный момент времени или мгновенной скоростью.

186 |
Глава 4. Дифференциальное исчисление |
Пример 13.1. Найти скорость равномерно ускоренного движения в произвольный момент времени t и в момент t = 3 с, если зависимость пути от времени выражается формулой S = gt2/2. Здесь g — ускорение свободного падения.
Решение. В момент времени t пройденный путь S = gt2/2, а в момент времени
t + t он равен S + S = g(t + |
t)2/2. Приращение пути за промежуток времени |
||||||||||||||||||
t |
|
|
|
|
|
|
|
gt2 |
|
|
|
|
|
1 |
|
|
|||
S = |
g |
|
|
|
t)2 |
− |
|
|
|
|
|
g(Δt)2. |
|||||||
|
(t |
+ |
|
|
= gt t + |
|
|||||||||||||
2 |
2 |
2 |
|||||||||||||||||
Составим отношение |
|
|
|
S |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
= gt + |
|
g t. |
|
|
|
||||||||
|
|
|
|
|
|
t |
2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тогда по определению будем иметь |
|
t→0 |
|
|
|
|
|
= |
|
||||||||||
|
t→0 |
|
|
t = |
|
2 |
|
|
|||||||||||
v = lim |
|
|
S |
|
lim |
gt + |
1 |
g t |
|
|
gt. |
||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
В момент времени t = 3 с имеем v(3) = gt t=3 = 3g ≈ 3 · 9,8 = 29,4 м/с.
Пример 13.2. При нагревании тела его температура T изменяется в зависимости от времени нагрева t по закону T = ln(1 + t). С какой скоростью нагревается тело в момент t1 = 5 с.
Решение. В момент времени t1 температура тела T1 = ln(1 + t1). В момент t2 = |
|||||||||||||||||||||||||
t1 + t температура тела |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
T2 = ln(1 + t2) = ln(1 + t1 + |
t). |
|
|
|
|
|
|
|
|
|||||||||||||
Вычитая T1 из T2, получим приращение температуры за время |
|
t: |
. |
||||||||||||||||||||||
T = ln(1 + t1 + |
t) − ln(1 + t1) = ln |
|
|
1 + t1 |
|
|
|
= ln 1 + 1 + t1 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 + t1 + |
t |
|
|
|
|
|
|
t |
|
|
|||||
Составим отношение |
|
|
T |
|
ln[1 + |
t/(1 + t1)] |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
= |
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
t |
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Это средняя скорость нагревания тела за время от t1 |
до t2 = t1 |
+ |
|
t. |
|
|
|||||||||||||||||||
Чтобы определить скорость нагревания тела в момент t1, найд¨ем предел сред- |
|||||||||||||||||||||||||
ней скорости нагревания при |
|
t → 0: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
v(t1) = lim |
T |
= |
lim |
ln[1 + |
t/(1 + t1)] |
= lim |
|
|
t |
|
= |
1 |
|
, |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
t→0 |
t |
t→0 |
|
|
|
t |
|
|
|
|
t→0 |
|
t(1 + t1) 1 + t1 |
||||||||||||
т.е. |
|
|
v(t1) t1=5 = |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
1 + 5 |
6 град/c. |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Касательная к кривой в данной точке. Угловой коэффициент касательной
Касательной к кривой в точке M этой кривой называется предельное положение секущей, проходящей через точку M и отличную от не¨ точку M1 кривой, когда точка M1 стремится по кривой к точке M.

13. Производная и дифференциал функции одной переменной |
187 |
|
Пусть заданы кривая y = f(x) x |
[a, b] |
|
и фиксированная точка M(x, y) этой |
кривой |
|
(рис. 54). Провед¨ем секущую через точки M и |
|
|
произвольную точку M1. Если точка M1 будет |
|
|
неограниченно приближаться по кривой к точке |
|
|
M, то положение секущей будет изменяться, и, |
|
|
когда точка M1 совпад¨ет с точкой M, она зай- |
|
|
м¨ет положение касательной N1MN к точке M. |
|
|
Итак, при некотором значении x функция имеет |
|
|
значение y = f(x). Зададим x некоторое прира- |
Рис. 54. |
|
щение x. Тогда значению аргумента x + x |
|
|
будет соответствовать значение функции y + y = f(x + |
x). Секущая M1MC |
образует с осью Ox угол ϕ такой, что y/ x = tg ϕ. Если |
x → 0, то точка M1 |
будет стремиться по кривой к точке M, секущая M1MC – к касательной N1MN, а угол ϕ – к углу α, который образует касательная к кривой в данной точке M с положительным направлением оси Ox. Угловой коэффициент касательной определяется соотношением
tg α = lim tg ϕ = |
lim |
y |
= |
lim |
f(x + |
x) − f(x) |
. |
(13.4) |
x |
|
|
||||||
x→0 |
x→0 |
|
x→0 |
x |
|
|||
Можно написать уравнения касательной и нормали к кривой y = f(x) в точке
M1(x1, y1):
1 |
(x − x1). |
(13.5) |
|
y − y1 = tg α(x − x1), y − y1 = − |
|
||
tg α |
|||
Производная функции одной переменной
Теперь дадим определение производной данной функции y = f(x), заданной на интервале ]a, b[.
Производной данной функции y = f(x) по аргументу x называется предел
отношения приращения y функции к приращению x аргумента, когда |
x → 0: |
|||
lim |
y |
= y = f (x), |
(13.6) |
|
x |
||||
x→0 |
|
|
||
если он существует и конечен.
Из определения следует правило нахождения производной функции: чтобы найти производную функции y = f(x), нужно
1) |
найти приращение функции y = f(x + |
x) − f(x) и составить отношение |
|
приращения y функции к приращению |
x аргумента; |
2) |
найти предел этого отношения при x → 0. |
|
Производную данной функции y = f(x) обозначают символами f (x) или y (по Лагранжу), или df/dx, dy/dx (по Лейбницу).
Пример 13.3. Найти производную от функции y = x3 в произвольной точке x и в точке x = 2. Написать уравнения касательной и нормали в этой точке.
Решение. 1. Найд¨ем приращение y функции y |
= x3: |
y = f(x + x) − f(x) = (x + |
x)3 − x3 = |

188 |
|
|
Глава 4. Дифференциальное исчисление |
|
= x3 + 3x2 x + 3x(Δx)2 + (Δx)3 − x3 = 3x2 x + 3x(Δx)2 + (Δx)3 |
||||
и составим отношение |
|
|
|
|
|
|
y |
= 3x2 + 3x(Δx) + (Δx)2. |
|
|
|
|
||
|
|
x |
||
2. Найд¨ем предел этого отношения при x → 0: |
||||
lim |
y |
= |
lim [3x2 + 3x(Δx) + (Δx)2] = 3x2 |
|
x |
||||
x→0 |
|
x→0 |
||
или y = (x3) = 3x2 — производная от функции y = x3.
3. Конкретное значение производной при x = a обозначается так: f (a) или |
||||||||||||||||||
y x=a. Для нашего случая |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
y |
x=2 = y (2) = 3x2 x=2 = 3 · 4 = 12. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С геометрической точки зрения y |
| |
x=2 равна |
угловому коэффициенту касательной |
|||||||||||||||
к кривой y = x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
в точке, где x = 2, т.е. tg α = 12. |
− |
|
− |
|
|||||||||||||
|
y |
8 = |
|
1 |
(x |
|
2) |
|
|
|
|
|
|
2), а |
||||
4. Поскольку y(x) |
x=2 |
= 23 = 8, то уравнение касательной: y |
|
8 = 12(x |
|
|||||||||||||
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
нормали: |
|
− |
|
|
− |
− . |
|
|
|
|
|
|
|
|
|
|||
Рассмотренные выше задачи, приводящие к понятию производной, после опре- |
||||||||||||||||||
деления производной (13.6) можно переформулировать следующим образом. |
||||||||||||||||||
В задаче о неравномерном прямолинейном движении мы нашли, что |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
lim |
S |
= v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
t→0 |
t |
|
|
|
|
|
|
есть скорость в момент t. Следовательно, S = dS/dt = v, т.е. производная от пути по времени есть скорость v точки, движущейся по прямой. Таков механический смысл производной. В общем случае производная есть скорость изменения функции в точке.
В задаче о касательной мы нашли, что
lim |
y |
= tg α |
||
x |
||||
x→0 |
|
|||
или |
dy |
|
|
|
y = |
|
= tg α, |
||
dx |
||||
|
|
|||
т.е. значение производной y при данном значении аргумента x равно тангенсу угла, образованного касательной к кривой y = f(x) в соответствующей точке M(x, y) и положительным направлением оси Ox. Таков геометрический смысл
производной. В силу этого уравнения касательной и нормали (13.5) запишутся |
||||
как |
1 |
|
|
|
y − f(x1) = f (x1)(x − x1), y − f(x1) = − |
|
|
(x − x1). |
|
|
|
|
||
f |
(x ) |
|||
|
1 |
|
|
|
Процесс вычисления производной от функции y = f(x) называется дифференцированием этой функции.

13. Производная и дифференциал функции одной переменной |
|
|
|
189 |
|||||||
x |
Показать, что функции |
|
, |
|
( |
|
|
|
), |
, |
, |
Пример 13.4. |
|
y = C |
|
y = xn |
|
n |
|
N |
|
y = sin x y = cos x |
|
y = a имеют производные в каждой точке x R, прич¨ем
1)y = (C) = 0;
2)y = (xn) = nxn−1, в частности при n = 1 y = x = 1;
3)y = (sin x) = cos x;
4)y = (cos x) = − sin x;
5)y = (ax) = ax ln a, в частности y = (ex) = ex при a = e.
Решение. Выше было показано, что все указанные функции определены и непрерывны в каждой точке x R. Следуя определению производной, имеем:
1) y = C, где C — постоянная, тогда y = C − C = 0 и поэтому
y = (C) = lim |
y |
= 0; |
|
x |
|||
x→0 |
|
2) y = xn, где n N, тогда, как было показано выше (см. формулу (12.22)),
и, следовательно, |
|
|
y = (x + x)n − xn = nxn−1 x + o(Δx) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
y = (xn) = lim |
|
y |
= |
lim |
nxn−1 |
x + o(Δx) |
= |
|
|
|
|||
|
|
|
|
|
|
|
|
||||||
x→0 |
x |
x→0 |
x |
|
|
||||||||
|
|
|
|
|
|
|
|
= lim (nxn−1 + o(1)) = nxn−1 + 0 = nxn−1; |
|||||
|
|
|
|
|
|
|
|
|
x→0 |
|
|
||
3) y = sin x: согласно примеру 12.2, |
|
|
|
|
|
||||||||
y = sin(x + |
x) − sin x = (cos x)Δx + o(Δx), |
x → 0, |
|||||||||||
следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
y = (sin x) = lim |
|
|
y |
|
= lim |
(cos x)Δx + o(Δx) |
|
= lim (cos x + o(1)) = cos x; |
|||||
|
|
x |
|
||||||||||
x→0 |
|
|
x→0 |
x |
x→0 |
|
|||||||
4) y = cos x: как и в примере 13.3, |
|
|
|
|
|
||||||||
y = cos(x + x) − cos x = cos x cos |
x − sin x sin |
x − cos x = |
|||||||||||
|
|
|
|
|
|
|
|
|
= cos x(cos |
x − 1) − sin x sin x, |
|||
тогда при x → 0
y = (− sin x)Δx + o(Δx)
и, следовательно,
y = (cos x) = lim |
|
y |
= |
lim |
|
(− sin x)Δx + o(Δx) |
= |
lim ( |
− |
sin x+o(1)) = |
− |
sin x; |
|||||
0 |
x |
0 |
x |
||||||||||||||
x |
→ |
|
x |
→ |
|
x |
→ |
0 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5)y = ax: как показано в разд. «Непрерывность функции одного аргумента», при x → 0
y = ax+Δx − ax = ax(a x − 1) = (ax ln a)Δx + o(Δx),
и, следовательно, |
|
|
|
|
|
|
|
y = (ax) = lim |
y |
= |
lim |
(ax ln a)Δx + o(Δx) |
= |
lim (ax ln a + o(1)) = ax ln a; |
|
x |
x |
||||||
x→0 |
|
x→0 |
|
x→0 |
