DIF_calc_2013

что и требовалось доказать.

Из примера 14.19,в) для x = e−t = ϕ(t), y = e2t = ψ(t) имеем ϕt = −e−t, ϕt = e−t, ψt = 2e2t, ψt = 4e2t, следовательно,

В заключение рассмотрим пример на вычисление производных высших порядков функций, заданных неявно.

Если нужно найти вторую производную от неявной функции, следует продифференцировать полученное для y равенство (снова рассматривая y как функцию от x), а затем заменить y его выражением, полученным при первом дифферен-

цировании. Аналогично находятся y , y(4) и т.д.

Пример 15.9. Найти y , если

arctg y + x − y = 0.

Решение. Продифференцируем неявно заданную функцию:

(arctg y) + x − y = 0,

т.е.

y + 1 − y = 0, 1 + y2

откуда

1 − 1 y = −1 1 + y2

или y = y−2 + 1.

Снова продифференцируем полученное выражение:

(y ) = (y−2) + 1 ,

т.е.

y = −2y−3y + 0,

откуда

y = −2y , y3

но

y = y12 + 1,

тогда

16.Теоремы о дифференцируемых функциях

Теорема 16.1 (Теорема Ролля о корнях производной). Если функция y = f(x) непрерывна на отрезке [a, b]; дифференцируема в промежутке ]a, b[ и принимает равные значения f(a) = f(b) на концах [a, b], то между a и b существует по крайней мере одна такая точка c, в которой производная этой функции обратится в нуль: f (c) = 0. Число c называется корнем производной функции f(x).

Доказательство. Так как функция f(x) непрерывна на [a, b], то она достигает на [a, b] своего наибольшего M и наименьшего m значений:

m f(x) M.

Если m = M, то f(x) в ]a, b[ сохраняет постоянное значение f(x) = M. Поэтому f (x) как производная постоянной равна нулю во всех точках ]a, b[, и за точку c можно взять любую точку этого отрезка. Если же M = m, то или M = 0, или

m = 0.

Пусть M > 0 и y = f(x) принимает наибольшее значение при x = c, т.е.

По условию теоремы, производная при x = c существует. Поэтому в пределе при x → 0 получим

Таким образом, мы пришли к противоречию: f (c) 0

и f (c) 0. Противоречие разрешимо в том случае, когда f (c) = 0. Следовательно, внутри [a, b] найд¨ется точка x = c, в которой f (c) = 0.

Теорема Ролля имеет следующую геометрическую интерпретацию: если непрерывная кривая, имеющая в каждой точке касательную (в этом случае говорят, что кривая гладкая), принимает равные значения на границах отрезка [a, b], то на этой кривой найд¨ется по край-

ней мере одна точка с абсциссой x = c, a < c < b, в которой касательная параллельна оси Ox (см. рис. 61).

♦ Если функция f(x) такова, что производная существует не во всех точках ]a, b[, то утверждение теоремы неверно, т.е. в этом случае между a и b нет такой

3

непрерывна на отрезке [−1, 1] и f(−1) = f(1) = 0, но е¨ производная

f (x) = 2

− √

3 3 x

в этом промежутке в нуль не обращается. Причина этого – внутри [−1, 1] существует точка x = 0, в которой производная не существует (обращается в бесконечность), и условия теоремы не выполнены.

Пример 16.1 Доказать, что на [−1, 2] для функции

f(x) = x3 + 4x2 − 7x − 10

справедлива теорема Ролля.

Решение. Действительно, на концах отрезка [−1, 2] значения функции совпадают: f(−1) = f(2) = 0. Вместе с тем функция как полином 3-го порядка на этом отрезке является непрерывной и дифференцируемой. Следовательно, все условия теоремы Ролля выполняются, поэтому на отрезке [−1, 2] существует по крайней мере одна точка c, в которой f (c) = 0. Теорема Ролля не указывает правило, по которому можно найти точку c в общем случае. Тем не менее, используя явный вид функции, мы можем найти точку c для конкретных функций. Так как

f (x) = 3x2 + 8x − 7,

то из уравнения

f (x) = 3x2 + 8x − 7 = 0

находим два корня:

√

из которых x2 ≈ 0,7 принадлежит отрезку [−1, 2], т.е. c = (−4 + 37)/3 ≈ 0,7. Теорему Ролля можно сформулировать и так: между двумя нулями диффе-

ренцируемой функции f(x) заключен по крайнем мере один нуль производной.

Теорема 16.2 (Лагранжа). Если функция y = f(x) непрерывна на отрезке [a, b] и дифференцируема в любой точке ]a, b[, то разность значений функции y = f(x) на концах [a, b] равна длине b−a отрезка [a, b], умноженной на производную функции, вычисленной для некоторого промежуточного среднего значения x = c, a < c < b, т.е.

Она удовлетворяет всем условиям теоремы Ролля: она непрерывна на [a, b], так как функция f(x) непрерывна на этом отрезке; она дифференцируема, т.е. имеет конечную производную

F (x) = f (x) − f(b) − f(a), b − a

так как существует конечная производная f (x) в ]a, b[; значения функции на концах промежутка равны, так как F (a) = F (b) = 0. Следовательно, согласно теореме Ролля, в ]a, b[ существует такая точка c, что F (c) = 0, откуда

f (c) − f(b) − f(a) = 0. b − a

Таким образом,

f(b) − f(a) = f (c), b − a

что и требовалось доказать.

Следствие 16.2.1. Если функция f(x) удовлетворяет условиям теоремы Лагранжа на отрезке [a, b] и f (x) = k, где k — постоянная, то f(x) — линейная функция:

Действительно, функция f(x) удовлетворяет теореме Лагранжа на любом отрезке [a, x] [a, b], и, следовательно, согласно формуле (16.6), f(x) − f(x) = k(x − a), что и требовалось доказать.

♦ Важным частным случаем следствия 16.2.1 является случай, когда k = 0. Тогда функция постоянна и f(x) = f(a).

Следствие 16.2.2. Если функции f1(x) и f2(x) дифференцируемы при b > x a

и удовлетворяют условиям f1(a) = f2(a), f1(x) > f2(x) при x > a, то f1(x) > f2(x)

при a < x < b.

[a, x] [a, b]. Тогда, согласно теореме Лагранжа, существует точка c [a, x] такая,

при x > 0.

224 Глава 4. Дифференциальное исчисление

Решение. а) Пусть f1(x) = ln(x + 1), f2(x) = x − x2/2, тогда f1(0) − f2(0) = 0. Для производных f1(x) = 1/(1 + x) и f2(x) = 1 − x справедливо неравенство

1/(x + 1) > 1 − x, так как при x > 0 это неравенство равносильно очевидному неравенству 1 > 1 − x2. Применив следствие 16.2.2 к функциям f1(x) и f2(x), получим неравенство ln(1 + x) > x − x2/2, что и требовалось показать.

б) Аналогично, пусть f1(x) = arctg x, f2(x) = x − x3/3, тогда f1(0) − f2(0) = 0. Для производных f1(x) = 1/(1 + x2) и f2(x) = 1 − x2 справедливо неравенство 1/(x2 + 1) > 1 − x2, так как это неравенство равносильно очевидному неравенству 1 > 1 − x4. Применив следствие 16.2.2 к функциям arctg x и x − x3/3, получим неравенство arctg x > x − x3/3, что и требовалось показать.

Теорема Лагранжа называется также теоремой о конечных приращениях, а равенство (16.6) — формулой Лагранжа.

♦ Формула Лагранжа да¨ет точное выражение для приращения функции f(x), поэтому е¨ и называют формулой конечных приращений в отличие от приближенного равенства

f(b) − f(a) ≈ f (a)(b − a),

где b − a = o(1) при b → a, которое иногда называют фор-

мулой бесконечно малых приращений.

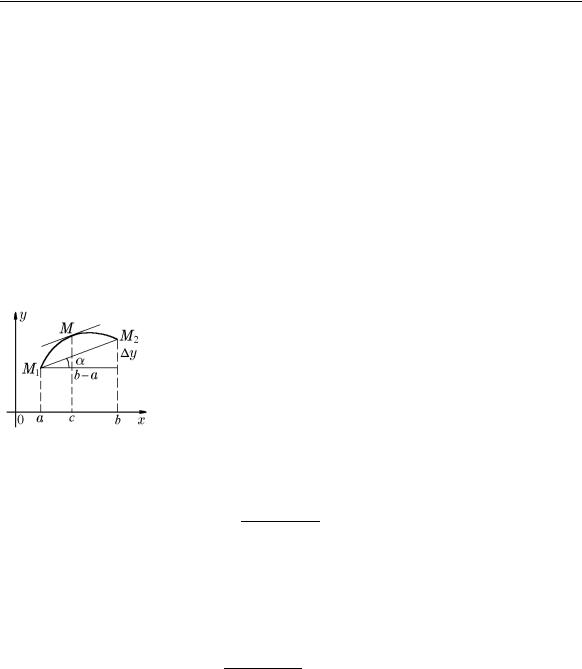
Теорема Лагранжа допускает следующую геометрическую интерпретацию: между двумя различными точками M1 и M2 непрерывной кривой y = f(x), имеющей касательную в каждой точке (гладкая кривая), существует хотя бы одна точка M с абсциссой x = c, в которой касательная параллельна хорде, соединяющей точки M1 и M2 (рис. 62).

По условию теоремы f(x) определена и непрерывна на [a, b] и дифференцируема в ]a, b[. Координаты точки M1[a, f(a)], а точки M2[b, f(b)]; x = c – абсцисса точки M.

Тогда угловой коэффициент хорды M1M2

k = f(b) − f(a) = tg α, b − a

а угловой коэффициент касательной в точке M

k1 = f (c).

Касательная параллельна хорде M1M2, поэтому k = k1 или

♦ Теорема Лагранжа утверждает: для непрерывной на [a, b] и дифференцируемой в ]a, b[ функции y = f(x) существует внутри этого интервала хотя бы одна точка c (a < c < b), для которой имеет место равенство (16.9), т.е. средняя скорость изменения функции совпадает с мгновенной скоростью в некоторой промежуточной точке x = c.

♦ Формула (16.6) имеет большое теоретическое значение, но малопригодна для практических расч¨етов, ибо она говорит о существовании числа c, но не указывает, как его найти. Лишь для линейной и квадратичной функций точка x = c всегда является серединой интервала ]a, b[, т.е. c = (a+b)/2. В других случаях положение точки x = c определяется конкретным видом функции f(x) и отрезком [a, b].

Формулу (16.6) можно записать в другом виде. Так как a < c < b, то отношение

c − a

b − a = θ

заключено между нулем и единицей, и поэтому можно записать

Теорема 16.3 (Коши). Если функции f(x) и ϕ(x) непрерывны на [a, b]; дифференцируемы в ]a, b[, т.е. имеют конечные производные f (x) и ϕ (x); производная ϕ (x) = 0 в ]a, b[, то найд¨ется хотя бы одна такая точка c внутри [a, b], что

Эта формула называется формулой Коши.

Доказательство. Так как ϕ (x) = 0 в ]a, b[, то из формулы Лагранжа для функции ϕ(x)

ϕ(b) − ϕ(a) = (b − a)ϕ (c)

следует, что ϕ(b) − ϕ(a) = 0 и на эту разность можно разделить. Составим вспомогательную функцию

Она удовлетворяет всем условиям теоремы Ролля. Действительно, F (x) непрерывна на [a, b], так как на [a, b] непрерывны, по условию, f(x) и ϕ(x). Функция F (x) дифференцируема, т.е. имеет конечную производную

F (x) = f (x) − f(b) − f(a) ϕ (x), ϕ(b) − ϕ(a)

так как в этом интервале существуют, по условию, конечные производные f (x) и ϕ (x). Наконец, F (a) = F (b) = 0. Следовательно, согласно теореме Ролля, существует внутри [a, b] такая точка x = c, что F (c) = 0. Таким образом,

f (c) − f(b) − f(a) ϕ (c) = 0, ϕ(b) − ϕ(a)

откуда