
DIF_calc_2013
.pdf


232 |
Глава 4. Дифференциальное исчисление |
Например, для f(x) = (1 + x)−1 при n = 2 и x0 = 0 |
|
|
|
1 |
= 1 − x + x2 + o(x2), |
|||||||
|
|
|
||||||||
|
1 + x |
|||||||||
где |
|
|
|
|
x3 |
|
|
|||
|
|
r2(x) = o(x2) = |
|
|
||||||
|
|
|
, |
|
|
|||||
так как |
1 + x |
|
|
|||||||
1 |
|
|
|
x3 |
||||||
o(x2) = |
− 1 + x − x2 = − |
|||||||||
|
|
|
. |
|||||||
|
1 + x |
1 + x |
||||||||
Для элементарных функций с уч¨етом (17.15)–(17.23) формулы Тейлора с оста-
точным членом в форме Пеано имеют вид |
|
|
|
|
|
||||||||||||||||||||
|
|
|
x2 |
|
xn |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ex = 1 + x + |
|
|
|
+ ... + |
|
|
+ o(xn); |
|
|
|
|
|
|||||||||||||
2! |
n! |
|
|
|
|
|
|||||||||||||||||||
sin x = x − |
x3 |
|
|
|
|
n x2n+1 |
|
|
2n+2 |
|
|
||||||||||||||
|
|
|
+ ... + (−1) |
|
|
|
|
|
+ o(x |
|
); |
|
|||||||||||||
3! |
(2n + 1)! |
|
|
||||||||||||||||||||||
|
|
x2 |
|
|
|
|
|
|
|
x2n |
|
|
|
|
(17.26) |
||||||||||
cos x = x − |
|
|
+ · · · + (−1)n |
|
|
+ o(x2n+1); |
|
||||||||||||||||||
|
2! |
(2n)! |
|
||||||||||||||||||||||
(1 + x)μ = 1 + μx + |
μ(μ − 1) |
x2 + ... + |
μ(μ − 1) · · · (μ − n + 1) |
xn + o(xn), |
|||||||||||||||||||||
|
|
|
|
|
|
|
x2 |
2! |
|
|
|
|
|
|
|
|
xn |
|
n! |
|
|||||
ln(1 + x) = x − |
x3 |
... + (−1)n−1 |
+ o(xn). |
|
|||||||||||||||||||||
|
+ |
|
+ |
|
|
|
|||||||||||||||||||
2 |
3 |
n |
|
||||||||||||||||||||||
18.Правило Лопиталя
Напомним, что если функция y = F (x), определ¨енная в проколотой окрестности точки a, становится неопредел¨енной в самой точке, то раскрытием неопредел¨енности называется отыскание предела функции F (x) при x → a.
При нахождении предела lim F (x) в результате непосредственной подстанов-
x→a
ки вместо x его предельного значения могут получиться неопредел¨енности семи видов:
0 |
, |
∞ |
, |
∞ − ∞ |
, 0 |
· ∞ |
, 00 |
, |
∞ |
0 |
, 1∞. |
0 |
|
|
|||||||||
|
∞ |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
Выше были приведены некоторые приемы раскрытия таких неопредел¨енностей. Однако существуют более общие способы раскрытия неопредел¨енностей, основанные на методах дифференциального исчисления.
Раскрытие неопредел¨енностей вида 0/0
Если F (x) = f(x)/ϕ(x) и f(x) → 0, ϕ(x) → 0 при x → a, то функция F (x) в точке a имеет неопредел¨енность вида 0/0.
Сформулируем так называемое правило Лопиталя для раскрытия неопредел¨енностей такого вида.
Теорема 18.1. Если функции f(x) и ϕ(x) непрерывны при x, близких к a, при таких x (но не равных a) имеют конечную первую производную, прич¨ем ϕ (x) =

18. Правило Лопиталя |
233 |
0, f(x) → 0 и ϕ(x) → 0 при x → a, то предел отношения этих функций при x → a равен пределу отношения производных этих функций, если последний предел (конечный или бесконечный) существует, т.е.
lim |
f(x) |
= lim |
f (x) |
. |
(18.1) |
|
|
||||
x→a ϕ(x) |
x→a ϕ (x) |
|
|||
Доказательство. Доопределим функции f(x) и ϕ(x) в точке a, положив f(a) = 0, ϕ(a) = 0. Тогда, выбрав некоторое значение переменной x (x = a), например x > a (или x < a), из окрестности точки a, можем утверждать, что на [a, x] функции f(x) и ϕ(x) непрерывны, внутри отрезка [a, x] они имеют конечные производные
и |
|
. Поэтому можно применить формулу Коши, согласно которой |
|
||||||||||
|
ϕ (x) = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(x) − f(a) |
= |
|
f (c) |
, a < c < x. |
|
|||||
|
|
|
|
|
|
|
|
||||||
|
|
|
ϕ(x) |
− |
ϕ(a) |
ϕ (c) |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как f(a) = 0 и ϕ(a) = 0, то |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
f(x) |
|
= |
f (c) |
|
(18.2) |
||
|
|
|
|
|
|
ϕ(x) |
ϕ (c) |
||||||
|
|
|
|
|
|
|
|
||||||
Если x → a, то так как a < c < x, то c тоже будет стремиться к a. Итак, переходя в (18.2) к пределу, получим
lim |
f(x) |
= lim |
f (c) |
= lim |
f (x) |
. |
|
|
|
||||
x→a ϕ(x) |
c→a ϕ (c) |
x→a ϕ (x) |
||||
По условию, этот предел существует, следовательно, существует и предел
lim f(x) ,
x→a ϕ(x)
и они равны.
Эта теорема справедлива и для случая, когда x → a = ±∞.
♦ Если отношение f (x)/ϕ (x) тоже приводит к неопредел¨енности вида 0/0, то можно снова применить правило Лопиталя, и, таким образом, в некоторых случаях для раскрытия неопредел¨енности приходится применять это правило последовательно несколько раз.
Пример 18.1. Найти
A1 |
= lim |
sin 4x |
, |
A2 |
= lim |
x − sin x |
. |
|
|
||||||
|
x→0 sin 2x |
|
|
x→0 |
x3 |
||
Решение. Имеем неопредел¨енность вида 0/0. Согласно правилу Лопиталя,
|
A1 = lim |
sin 4x |
= lim |
(sin 4x) |
= lim |
4 cos 4x |
= |
4 |
= 2; |
|
|
|||||||||
|
|
|
(sin 2x) |
|
|
2 |
|
|
||||||||||||
|
|
x→0 sin 2x |
x→0 |
x→0 |
2 cos 2x |
|
|
|
|
|||||||||||
A2 |
= lim |
x − sin x |
= lim |
1 − cos x |
|
= lim |
sin x |
|
= lim |
cos x |
= |
1 |
. |
|||||||
|
|
|
|
6 |
||||||||||||||||
|
x→0 |
x3 |
x→0 |
3x2 |
x→0 |
6x |
x→0 |
|
|
6 |
|
|
||||||||



236 Глава 4. Дифференциальное исчисление
Решение. Имеем неопредел¨енность вида ∞/∞. Согласно правилу Лопиталя, этот предел равен
lim |
x + sin x |
= lim |
1 + cos x |
, |
(18.3) |
|
x |
1 |
|||||
x→∞ |
x→∞ |
|
|
если последний предел существует. Но он не существует, следовательно, и равенство (18.3) записать нельзя. Однако это не означает, что не существует и предел отношения самих функций. Действительно,
x→∞ |
x |
|
= x→∞ |
|
|
x |
= 1 + x→∞ |
x |
|||||
lim |
x + sin x |
|
lim |
|
1 + |
sin x |
|
|
|
lim |
sin x |
. |
|
|
|
|
|
|
|
|
|
||||||
Положим α = 1/x. Тогда α → 0 при x → ∞, и |
|
|
|
|
|
||||||||
1 + lim |
sin x |
= 1 + lim α sin |
1 |
= 1 + 0 = 1. |
|
||||||||
x |
α |
|
|||||||||||
|
x→∞ |
|
|
α→0 |
|
|
|
|
|||||
Таким образом, при раскрытии этой неопредел¨енности правило Лопиталя оказалось неприменимым.
Раскрытие неопредел¨енностей вида 0 · ∞ и ∞ − ∞
Неопредел¨енности видов 0 · ∞ и ∞ − ∞ можно привести к неопредел¨енностям вида 0/0 или ∞/∞, к которым применимо правило Лопиталя.
Пусть f(x)ϕ(x) да¨ет неопредел¨енность 0·∞, когда lim f(x) = 0 и lim ϕ(x) = ∞.
x→a x→a
Представив функцию f(x)ϕ(x) в виде
f(x) f(x)ϕ(x) = 1/ϕ(x),
мы получим в точке a неопредел¨енность вида 0/0:
lim f |
x ϕ x |
|
|
lim |
|
f(x) |
= |
0 |
, |
|
|
||
|
|
|
|
|
|
|
|
||||||
x→a |
( ) ( ) = 0 · ∞ = x→a 1/ϕ(x) |
0 |
|
|
|
||||||||
для раскрытия которой можно применять правило Лопиталя. |
|
( ) = ∞, |
|||||||||||
Пусть имеем выражение |
f(x) |
− |
ϕ(x) |
, прич¨ем |
x→a |
( ) = ∞ и |
x→a |
||||||
|
|
|
|
|
lim f |
x |
lim |
ϕ x |
|||||
и, следовательно, это выражение становится неопредел¨енностью вида ∞ − ∞ в точке a. Тогда, написав это выражение в виде
f(x) − ϕ(x) = 1/f(x) |
− 1/ϕ(x) |
= |
ϕ(x) |
− f(x) |
&f(x) ϕ(x) , |
||
1 |
1 |
|
1 |
1 |
1 |
1 |
|
получим неопредел¨енность вида 0/0, для раскрытия которой можно применять правило Лопиталя.
Пример 18.7. Найти
x→0 |
sin x |
− x + x2 |
|
lim |
1 |
1 |
. |
|
|


19. Исследование функции |
239 |
19.Исследование функции
Если функция f(x) постоянна на некотором интервале (f(x) = C), то е¨ производная f (x) равна нулю во всех точках этого интервала. Справедливо и обратное утверждение, вытекающее из теорем о дифференцируемых функциях, а именно следствия 16.2.1 из теоремы Лагранжа 16.2.
Таким образом, для того чтобы в некотором промежутке функция сохраняла постоянное значение, необходимо и достаточно, чтобы производная от этой функции в промежутке равнялась нулю. Это и есть признак постоянства функции в промежутке. Рассмотрим теперь признаки возрастания и убывания функции.
19.1.Признаки возрастания и убывания функции
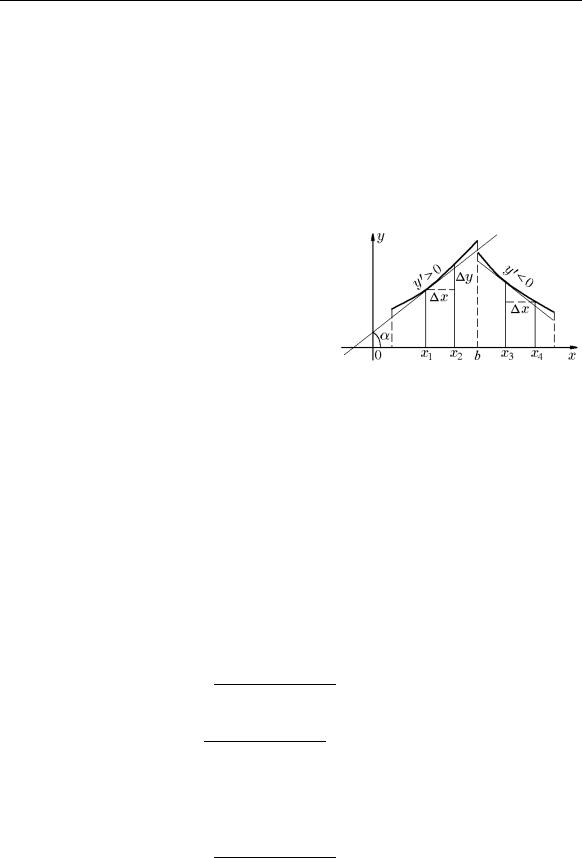
В разделе «Понятие функции одного вещественного переменного» были выделены классы возрастающих и убывающих на интервале функций, объедин¨енных названием
«монотонные» и содержащих подмножество |
|
строго монотонных, т.е. строго возрастающих |
|
и строго убывающих функций (рис. 63). Сфор- |
|
мулируем критерии, позволяющие найти об- |
|
ласти возрастания и убывания дифференци- |
Рис. 63. |
руемых функций. |
Теорема 19.1. Для того чтобы дифференцируемая на интервале ]a, b[ функция f(x) была неубывающей (невозрастающей) на этом интервале, необходимо и достаточно, чтобы е¨ производная была неотрицательна (неположительна) на этом интервале:
f (x) 0 (f (x) 0) для x ]a, b[. |
(19.1) |
Доказательство провед¨ем для возрастающей функции (доказательство для убывающей функции аналогично).
Необходимость. Действительно, выбрав точку x, принадлежащую интервалу [a, b], и придав x положительное приращение x, столь малое, чтобы точка x+Δx не выходила за границы [a, b], можем написать, что
|
f(x + x) − f(x) 0, |
|
|||
так как по условию функция не убывает. Но тогда и |
|
||||
|
f(x + |
x) − f(x) |
0, |
(19.2) |
|
|
|
||||
|
|
x |
|
||
а также |
x) − f(x) |
|
|
|
|
lim |
f(x + |
= f (x) 0. |
|||
|
|||||
x→0 |
x |
|
|||
Если x совпадает с правым концом отрезка, то взяв |
x < 0, будем иметь |
||||
f(x + x) − f(x) 0,
но
f(x + x) − f(x) 0, x
