DIF_calc_2013

Утверждение доказано.

Здесь мы воспользовались свойством сохранения знака нестрогого равенства при предельном переходе.

Достаточность. Пусть для всех x ]a, b[ выполняется условие f (x) 0 и пусть x1 < x2 — произвольные точки этого интервала. Применив к функции f(x) на отрезке [x1, x2] теорему Лагранжа, получим

f(x2) − f(x1) = f (c)(x2 − x1),

где f (c) 0, так как c [x1, x2] ]a, b[. Поскольку x1 и x2 — произвольные точки интервала ]a, b[, удовлетворяющие условию x1 < x2, то, согласно определению, f(x) — возрастающая на ]a, b[ функция, что и требовалось доказать.

Если в теореме 19.1 нестрогие неравенства (19.1) заменить строгими, то эти условия будут являться только достаточными, но не необходимыми. Действительно, функция y = x3 является строго возрастающей на R, но в точке x = 0 е¨ производная y = 3x2 обращается в нуль (y = 0), и строгое неравенство y > 0 нарушается. Поэтому для строго монотонных функций следующая теорема фор-

то функция f(x) строго возрастает (строго убывает) на интервале ]a, b[.

Доказательство провед¨ем для условия f (x) > 0. Пусть x1 < x2 — произвольные точки интервала ]a, b[. Согласно теореме Лагранжа

f(x2) − f(x1) = f (c)(x2 − x1), c ]a, b[.

Поскольку f (c) 0 и x2 − x1 > 0, то f(x2) − f(x1) > 0. Это и означает, что функция f(x) строго возрастает на интервале ]a, b[.

Доказанная теорема позволяет легко установить, что функция y = th x строго возрастает на R, поскольку y = 1/ ch2 x > 0 для всех x R.

Если функция f(x) удовлетворяет условию (19.3) не на интервале ]a, b[, а на отрезке [a, b], то справедлива следующая теорема.

Теорема 19.3. Если функция f(x) непрерывна на отрезке [a, b], дифференцируема на интервале ]a, b[ и удовлетворяет условию f (x) > 0 (f (x) < 0), то эта функция строго возрастает (строго убывает) на отрезке [a, b].

Доказательство аналогично доказательству теоремы 19.2 с той лишь разницей, что формула Лагранжа применяется к функции f(x) не на отрезке [x1, x2] ]a, b[, а на отрезке [a, b].

♦ Промежутки, в которых f (x) > 0, есть промежутки возрастания функции, а промежутки, в которых f (x) < 0, есть промежутки убывания функции. Геометрически это можно интерпретировать так: из рис. 63 ясно, что на промежутке возрастания функции касательная образует с осью Ox острый угол, тангенс которого положителен. Но tg α есть первая производная yM , т.е. на участке возрастания y = tg α > 0, соответственно, на промежутке убывания y = tg α < 0.

Пример 19.1. Исследовать на возрастание и убывание (найти интервалы строгой монотонности) функцию y = x2 − 5x + 3.

Решение. 1. Область существования – вся ось Ox.

функция строго возрастает. Там, где y = 2x − 5 < 0, функция f(x) убывает. Из неравенства 2x − 5 < 0, x < 5/2 следует, что функция f(x) убывает в ] − ∞, 5/2[, т.е. функция в этом интервале строго убывает (рис. 64).

Пример 19.2. Исследовать на возрастание и убывание функцию y = x22−x.

Решение. Производная y = x2−x(2−x ln 2) в точках x1 = 0 и x2 = 2/ ln 2 обращается в нуль, и y (x) > 0 для всех x ]0, 2/ ln 2[. Следовательно, на этом интервале функция возрастает. Производная принимает отрицательные значения (y (x) < 0) при x < 0 и x > 2/ ln 2. Следовательно, функция убывает для всех x, принадлежащих интервалам ] − ∞, 0[ и ]2/ ln 2, +∞[.

Пример 19.3. Показать, что функция y = (1 + 1/x)x возрастает на интервалах

] − ∞, −1[ и ]0, +∞[.

Зафиксируем переменную x = x0 > 0. На отрезке [x0, x0 + 1] к заданной функции y = f(x) применим формулу конечных приращений: x = x0 + 1 − x0 = 1, тогда

Учтем, что y(x) > 0 и 1/c > 1/(x0 + 1), и из (19.4) найд¨ем

Поскольку точка x = x0 > 0 выбрана произвольно, то последнее условие означает, что исследуемая функция на промежутке x > 0 является возрастающей.

Для второго интервала −∞ < x < −1 производную (19.4) запишем в виде

Это означает, что исследуемая функция на промежутке x > −1 также является возрастающей, что и требовалось доказать.

Пример 19.4. Обязательно ли производная монотонной функции является монотонной?

Решение. Не обязательно. Например, производная функции y = 3x + cos x положительна (y (x) = 3 − sin x > 0) и функция монотонно возрастает на R. В то же время производная функции y (x) = 3 − sin x на R, очевидно, не является монотонной (впрочем, это же следует из того, что [y (x)] = − cos x является знакопеременной функцией).

19.2. Экстремумы функций

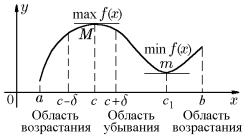
Пусть функция f(x) задана в некотором интервале ]a, b[ (рис. 65). Рассмотрим точки M и m, абсциссы которых соответственно равны c и c1. Область определения ]a, b[ функции (см. рис. 65) разбивается на промежутки, на которых функция возрастает или убывает. Так, ]a, c[ – интервал возрастания функции, на котором y = f (x) > 0, а ]c, c1[ – интервал убывания функции, на котором y = f (x) < 0, и интервал ]c1, b[ – интервал возрастания функции f(x), на котором снова y = f (x) > 0.

Те точки, которые отделяют промежутки возрастания функции от промежутков е¨ убывания (или наоборот), являются вершинами кривой y = f(x).

Таким образом, необходимо отличать максимум функции от точки максимума. Аналогично рассмотрим вершину m кривой. Ордината этой точки f(c1) меньше всех соседних с ней ординат, лежащих как слева, так и справа от точки c1, как говорят, в окрестности точки c1: c1 − δ < c1 < c1 + δ. Тогда говорят, что этой вершине соответствует минимум функции.

Частное значение f(c1) функции f(x) во внутренней точке c1 (см. рис. 65) некоторого интервала называется локальным минимумом (min) функции f(x), если существует δ > 0 такое, что для всех x, таких, что 0 < |x−c1| < δ справедливо

f(c1) < f(x).

Вместо отдельных наименований «локальный максимум» и «локальный минимум» употребляют объединяющее их наименование «локальный экстремум», что в переводе с латинского означает «крайнее» (значение).

Теорема 19.4. Если дифференцируемая функция f(x) имеет локальный экстремум в точке c, то е¨ производная в этой точке равна нулю: f (c) = 0.

Доказательство. Пусть c — точка максимума. Рассмотрим δ-окрестность этой точки c − δ < c < c + δ в которой справедливо f(c) > f(x). Для точки максимума

f(x) − f(c) < 0, x < c,

и отношение

f(x) − f(c) > 0 x − c

есть величина положительная. Переходя к пределу при x → c, с уч¨етом дифференцируемости получим

Если же x > c, то x − c > 0, f(x) − f(c) < 0, и, следовательно, отношение

Получаем, что 0 f (c) 0. Полученное противоречие может быть разрешено только при f (c) = 0.

Итак, в точке локального максимума производная дифференцируемой функции обращается в нуль (f (c) = 0). Геометрически это означает, что касательная в этой точке параллельна оси Ox:

y x=c = tg α = 0.

Аналогично доказывается, что в точке x = c1, где функция f(x) имеет локальный минимум, справедливо f (c) = 0. Таким образом, утверждение теоремы доказано.

Доказанная теорема обосновывает алгоритм нахождения точек локальных экстремумов дифференцируемой функции, а именно: точки локальных экстремумов следует искать среди точек, в которых производная f (x) обращается в нуль. Если функция является кусочно-непрерывной и не дифференцируема в точках xk,

k = 1, N, то для определения локальных экстремумов помимо точек, в которых производная f (x) обращается в нуль, следует рассматривать также точки, в которых производная f (x) либо обращается в бесконечность, либо не существует.

Например, функция y = |x| в точке x = 0 производной не имеет, но имеет

локальный минимум y x=0

y (0) = ∞.

Далее при формулировке утверждений, связанных с локальными экстремумами, слово «локальный» зачастую (для простоты) может опускаться.

Точки, в которых производная функции равна нулю, называются стационарными точками, а точки, в которых функция непрерывна, а е¨ производная равна нулю либо обращается в бесконечность, либо не существует, — е¨ критиче-

скими точками.

Таким образом, все точки экстремумов непрерывной функции являются также е¨ критическими точками. Однако не всякая критическая точка является точкой экстремума функции. Так, например, точка x = 0 является критической точкой для функций y = x2, y = x3, y = |x|, y = |x|1/2, y = x1/3. Но для функций y = x2,

y = |x|, y = |x|1/2 точка x = 0 — точка экстремума, а для функций y = x3, y = x1/3 эта точка не является точкой экстремума.

Рис. 66.

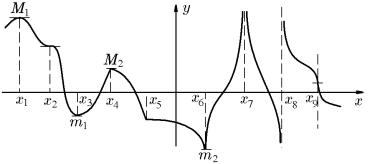
На рис. 66 показана функция с критическими точками различных типов. Первые три точки являются стационарными, в этих точках производная обращается в нуль: f (x) = 0. Следующие две точки являются критическими: в этих точках производная f (x) не существует. Остальные точки — критические, в которых f (x) = ±∞. Более подробно:

1) x1 — точка максимума (f (x1) = 0);

2) x2 не является точкой экстремума (f (x2) = 0); 3) x3 — точка минимума (f (x3) = 0);

4) x4 — точка максимума (f (x4) не существует);

5) x5 не является точкой экстремума (f (x5) не существует); 6) x6 — точка минимума (f (x6) → ±∞);

7) x7 не является точкой экстремума (f (x7) → ±∞); 8) x8 не является точкой экстремума (f (x8) → −∞); 9) x9 не является точкой экстремума (f (x9) → +∞).

Перейд¨ем к рассмотрению достаточных условий экстремумов.

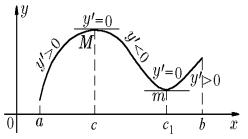
Теорема 19.5 (1-ое достаточное условие экстремума). Пусть функция y = f(x) непрерывна в точке x = c и дифференцируема в некоторой е¨ окрестности кроме, может быть, самой точки c. Тогда, если f (x) меняет знак с плюса на минус при переходе через точку c, то эта точка является точкой максимума; если же f (x) меняет знак с минуса на плюс, то точка c — точка минимума (см. рис. 67).

Доказательство. Пусть производная f (x) функции f(x) меняет знак с плюса на минус при переходе через точку c, тогда существует δ-окрестность точки c, в

Аналогично, применив теорему Лагранжа к функции f(x) на отрезке [c, x], где c < x < c + δ, получим, что

Совокупность условий (19.7) и (19.8) эквивалентна определению локального экстремума функции f(x) в точке x = c, что и доказывает первую часть теоремы. Аналогично доказывается второе утверждение теоремы.

Доказанная теорема позволяет сформулировать первое практическое правило, позволяющее находить точки экстремума:

1)для исследуемой функции y = f(x) вычисляем производную y (x) и находим е¨ критические точки, в которых производная y (x) обращается в нуль, бесконечность или вовсе не существует;

2)исследование знаков производной y (x) до и после каждой критической точки позволяет либо установить характеристику экстремума по типу изменения знака, либо отнести е¨ к интервалу монотонности в случае сохранения знака y (x).

Это правило полностью решает вопрос о нахождении точек экстремума, когда в рассматриваемом промежутке ]a, b[ имеется лишь конечное число критических

точек xi, i = 1, N. Тогда в любом промежутке

]a, x1[, ]x1, x2[, . . . , ]xn, b[

существует конечная производная y (x) и, кроме того, в каждом таком промежутке y (x) сохраняет постоянный знак, определяющий характер монотонности. Последнее замечание бывает полезным в некоторых случаях на практике: знак производной y (x) во всем промежутке ]xi, xi+1[ можно определить, установив его в одной какой-либо точке этого промежутка.

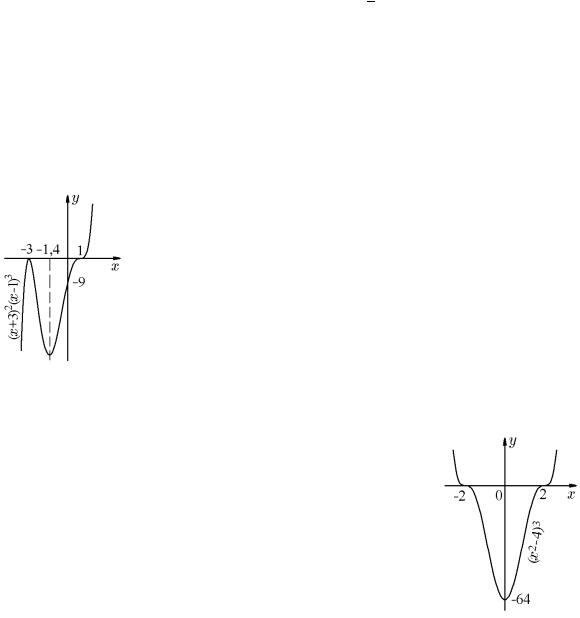
Пример 19.5. Найти экстремумы функции

f(x) = (x + 3)2(x − 1)3.

непрерывны на всем промежутке ] − ∞, +∞[. Для определения критических (стационарных) точек производную (19.9) приравняем к нулю:

f (x) = 5(x + 3)(x − 1)2 x + 75 = 0.

Решениями этого уравнения являются три точки: x1 = −3, x2 = −1,4, x3 = 1, которые весь промежуток ] − ∞, +∞[ разбивают на четыре интервала: ] − ∞, −3[,

] − 3; −1,4[, ] − 1,4; 1[, ]1, +∞[. Методом интервалов определяем знак производной:

растает, а на интервале ] − 3; −1,4[ убывает. Точка x1 = −3, отделяя интервал возрастания от интервала убывания, является точкой максимума, в которой функция достигает локального максимума, равного fmax(−3) = −9. Следующая критическая точка x2 = −1,4 отделяет интервал убывания ] −3; −1,4[ от интервала возрастания ] −1,4; 1[ и, следовательно, является точкой минимума, в которой функция достигает локального минимума, равного fmin(−3) = −35,39. При переходе через третью критическую точку x3 = 1 знак производ-

Рис. 68. ной f (x) не меняется, и, следовательно, эта точка не является точкой экстремума. На рис. 68 привед¨ен схематический гра-

фик, иллюстрирующий поведение исследуемой функции.

Пример 19.6. Исследовать на экстремум функцию

f(x) = (x2 − 4)3.

Решение. Данная функция и е¨ производная

непрерывны на всем промежутке ] − ∞, +∞[. Для определения критических (стационарных) точек производную (19.10) приравняем к нулю:

Решениями этого уравнения являются три точки: x1 = −2, x2 = 0, x3 = 2, которые промежуток ] − ∞, +∞[ разбивают на четыре интервала: ] − ∞, −2[, ] − 2, 0[, ]0, 2[, ]2, +∞[. Очевидно, что знак производной (19.11) изменится с отрицательного на

положительный только при переходе через точку x2 = 0, поскольку 6(x2 −4)2 0. Это означает, что точка x2 = 0 отделяет интервал убывания ] − ∞; 0[ от интервала возрастания ]0, +∞[ и, следовательно, является точкой минимума, в которой функция достигает локального минимума, равного fmin(0) = −64. Критические точки x2 = −2 и x3 = 2, при переходе через которые производная знак не меняет, принадлежат интервалу монотонности и не являются точками экстремума. На рис. 69 привед¨ен схематический график функции.

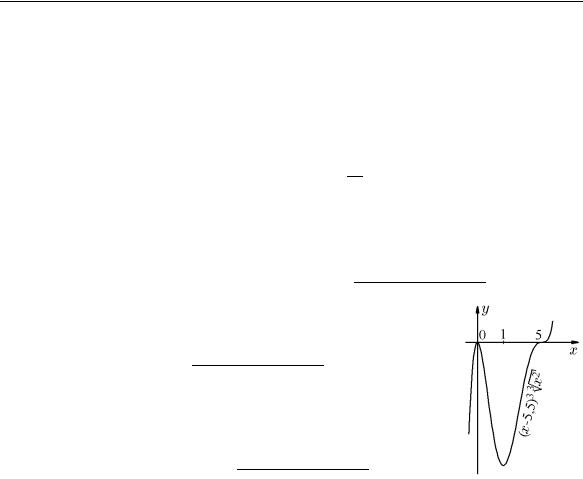
Пример 19.7. Исследовать на экстремум функцию

√

f(x) = (x − 5,5)3 3 x2.

Решение. Функция непрерывна на всем промежутке ] − ∞, +∞[. Чтобы найти критические точки, вычислим производную:

√

3 3 x

Рис. 70.

Отсюда найд¨ем ещ¨ две критические (стационарные) точки: x2 = 1, x3 = 5,5.

Из (19.12) видно, что знак производной f (x) может изменяться только при

переходе через точки x1 = 0 и x2 = 1, поскольку множитель (x − 5,5)2 0 неотрицателен. Следовательно, критическая точка x3 = 5,5 принадлежит интервалу монотонности и не является точкой экстремума. Чтобы определить характер критических точек x1 и x2, установим тип изменения знака производной при прохождении через эти точки и результат свед¨ем в таблицу:

в точке x = 0.

248 Глава 4. Дифференциальное исчисление

Решение. 1) Функция f(x) непрерывна на всей числовой оси ]−∞, ∞[, поскольку

В точках, отличных от точки x = 0, производная функции f(x) вычисляется

Однако производная (19.13) не определена в точке x = 0. В этом случае следует воспользоваться определением производной. Получим

Это означает, что точка x = 0 является критической. Однако в любой окрестности точки x = 0 производная (19.13) бесконечное число раз меняет знак как слева, так и справа от точки x = 0, что не позволяет применить теорему 19.5, чтобы определить характер критической точки. Исследуя непосредственно функцию x2 sin(1/x), видим, что и сама функция в любой окрестности (в том числе и бесконечно малой) точки x = 0 бесконечное число раз меняет знак как слева, так и справа от точки x = 0. Следовательно, точка x = 0 не является точкой экстремума.

2) Функция f(x) непрерывна на всем интервале ] − ∞, ∞[, поскольку

В точках, отличных от точки x = 0 е¨ производная вычисляется стандартным образом:

Однако производная (19.14) не определена в точке x = 0. В этом случае воспользуемся определением производной:

Это означает, что точка x = 0 является критической. Однако в любой близости от точки x = 0 производная (19.14) слева и справа от точки x = 0 меняет знак бесконечное число раз, что не позволяет воспользоваться теоремой 19.5 для определения характера критической точки x = 0. Явный вид самой функции f(x) показывает, что точка x = 0 является точкой минимума, поскольку f(0) = 0, а f(x) > 0 для всех x = 0.

Последний пример показывает, что смена знака производной f (x) при переходе через точку x0 не следует из того, что x0 является точкой экстремума функции f(x). Таким образом, теорема, обратная теореме 19.5, неверна.

Сформулируем ещ¨ одно достаточное условие существования экстремума.

Теорема 19.6 (2-ое достаточное условие существования экстремума).

Если x0 — стационарная точка функции f(x) и существует f (x0), то x0 — точка локального минимума при условии f (x0) > 0 и x0 — точка локального максимума при условии f (x0) < 0.

Доказательство. Если x0 — стационарная точка, то f (x) = 0. Пусть f (x0) > 0, тогда существует некоторая окрестность S(x0, δ) точки x0, в которой функция f (x) возрастает, т.е. выполняются условия

из которых следует, что функция f (x) меняет знак с минуса на плюс при переходе через точку x0. Согласно теореме 19.5, такое чередование знаков означает, что точка x0 — точка минимума функции f(x). Аналогично доказывается случай f (x) < 0 (см. рис. 67).

Пример 19.9. Исследовать на экстремум функцию f(x) = x3 − x2 − x.

Решение. 1. Находим первую производную:

f (x) = (x3 − x2 − x) = 3x2 − 2x − 1

иприравниваем е¨ к нулю.

2.Решив уравнение

3x2 − 2x − 1 = 0,

найд¨ем корни: x1 = 1, x2 = −1/3. 3. Найд¨ем вторую производную

f (x) = (3x2 − 2x − 1) = 6x − 2

и вычислим е¨ значения в критических точках: f (1) = 4 > 0 и f (−1/3) = −4 < 0. Следовательно, x1 = 1 — точка минимума, а x2 = −1/3 — точка максимума. И, наконец,

19.3.Наибольшее и наименьшее значения функции на отрезке

Если функция f(x) непрерывна на [a, b], то в силу непрерывности она принимает на этом отрезке как наибольшее M, так и наименьшее m значения.

Если функция принимает наибольшее значение в одной из внутренних точек, то оно будет одним из максимумов функции и при этом наибольшим, называемым глобальным максимумом на [a, b]. Но наибольшее значение функция может принимать и на одной из границ отрезка. Поэтому, чтобы найти наибольшее значение функции на отрезке [a, b], нужно

1)найти все максимумы;

2)вычислить значения функции f(a) и f(b) на границах отрезка [a, b];

3)из всех найденных значений функции выбрать наибольшее, оно и будет являться наибольшим значением функции на [a, b].