1.6 Непрерывные случайные величины

1.6.1 Основные свойства и характеристики

В предыдущем параграфе рассматривались дискретные случайные величины, для которых множество исходов конечно. Если значения случайной величины целиком заполняют некоторый интервал, то случайная величина называется непрерывной.

При операциях с дискретными случайными величинами мы пользовались рядами распределения. Для непрерывной случайной величины вместо них вводятся функция распределения и плотность вероятностей.

Функцией распределения непрерывной случайной величиныназывают функциюF(х), определяющую вероятность того, что случайная величина ζ примет значение, меньшее, чемх,

. (1.14)

Она обладает следующими основными свойствами:

-значение функции принадлежит отрезку [0;1], т.е.;

-функция является неубывающей, т.е. , прих₂ > х₁;

-вероятность того, что случайная величина примет значение, заключенное в интервале (а, b), равна приращению функции на этом интервале, т. е..

Наряду с функцией распределения F(x) в теории вероятностей используется так называемаяплотность вероятностей, равная производной от этой функции:

f (x) =F ^/(x). (1.15)

Плотность вероятностей обладает следующими свойствами:

а) б); в).

Рассмотрим пример. Пусть f (х) имеет следующий вид:

Тогда графическое изображение f (х) иF(х) для этой функции имеют вид, приведенный на рисунках.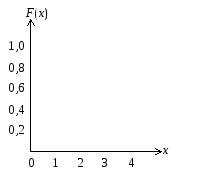

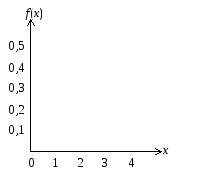
а) б)

Рисунок 1.2 – Функция распределения (а) и плотность

вероятностей (б)

1.6.2 Числовые характеристики непрерывных случайных величин

Для непрерывных случайных величин вводятся следующие числовые характеристики:

-математическое ожиданиенепрерывной случайной величиныХ, возможные значения которой принадлежат всей числовой оси, определяется по формуле

. (1.16)

-дисперсия и среднеквадратичное отклонениенепрерывной случайной величиныХ;определяются формулами

;

(1.17)

.

Задача.Определить математическое ожидание, дисперсию и среднеквадратичное отклонение для случайной величиныХ, плотность вероятностей которой представлена на рис. 12.2,б.

Решение: по формулам (1.16) и (1.17) с учетом графиков на рисунке 1.12 находим

;

; .

^{1.6.3 Основные законы распределения}

Вероятностные методы исследований имеют широкое применение в науке. Поэтому студентам важно знать наиболее распространенные функции распределения случайных величин и условия, когда они используются. Характеристики этих распределений представлены в таблице 1.4, а вид плотности вероятностей – на рисунке 1.3.

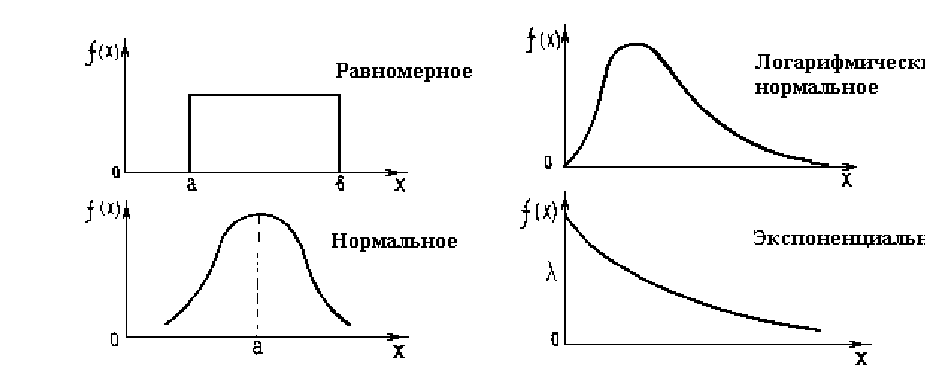
1.3 – Плотности распределения случайных величин

Таблица 1.4 – Основные законы и характеристики распределений

Распределение	Область значений	Плотность Распределения	Среднее	Дисперсия
Равномерное	(а, в)
Нормальное			А
Логнормальное
Показательное

Наиболее распространенным является нормальное распределениеслучайных величин. Ему подчиняются стабильные характеристики социально – экономических процессов, параметры объектов и совокупностей, когда они меняются в небольших пределах.

Логарифмически – нормальное(логнормальное) распределение используется обычно, когда распределение мало отличается от нормального, но среднее значение случайной величины близко к нулю и не уходит в отрицательную область.

Равномерно распределеннымина интервале (а, b) обычно принимаются вероятностные параметры , исходная информация о распределении которых мала, но известен примерный диапазон, в котором они изменяются.

Экспоненциальное (показательное) распределение используется при решении задач надежности функционирования технических и социально-экономических систем, оценки их безопасности и эффективности .

Особое место среди законов распределения случайных величин занимает нормальное распределение. Закону нормального распределения подчиняется большинство совокупностей, изучаемых в прикладных науках. Поэтому изучению его закономерностей посвящен отдельный подраздел.