
- •С.П. Казаков
- •Содержание
- •1. Элементы теории вероятностей
- •1.1. Общие понятия
- •1.2. Сумма и произведение случайных событий,
- •1.3 Формула полной вероятности, формула Байеса
- •1.4 Схема Бернулли
- •1.5 Дискретные случайные величины
- •1.6 Непрерывные случайные величины
- •1.6.2 Числовые характеристики непрерывных случайных величин
- •1.3 – Плотности распределения случайных величин
- •1.7 Нормальное распределение
- •1.8 Основы теории надежности
- •1.8.2. Надежность элементов
- •Контрольные вопросы и задачи
- •2. Случайные прцессы
- •2.1Общие понятия
- •2.2 Непрерывный нормальный
- •2.3 Нестационарный случайный процесс (временной ряд)
- •2. 4 Марковские случайные процессы
- •Самостоятельная работа № 2
- •3. Математическая статистика
- •3.1 Общие понятия и задачи математической статистики
- •3.2 Выборочный метод
- •175, 166, 169, 179, 164, 170, 169, 167, 175, 181.
- •158, 162, 163, 164, 165, 166, 167, 168, 169,169,
- •170, 170, 171, 174, 175, 175, 177, 179, 180, 181.
- •3.3 Точечные оценки параметров распределений
- •3.4 Доверительные интервалы
- •3.5 Отсев грубых ошибок и определение минимально
- •3.6Проверка статистических гипотез
- •6, 4, 5, 7, 6, 4, 8, 6, 8, 9. 3, 2, 0, 4, 4, 3, 4, 1, 5, 7.
- •3, 6, 3, 4, 6, 9, 4, 9, 6, 5. 3, 4, 6, 4, 2, 3, 6, 3, 4, 1.
- •4 Статистические зависимости и связи
- •4.1 Подбор эмпирических формул (парная корреляция)
- •4.2 Практическая задача: проверка легитимности выборов
- •4.3 Множественная корреляция
- •4.4 Задачи классификации
- •Теория вероятностей, случайные процессы и математическая статистика
4.3 Множественная корреляция
Под множественной
корреляцией понимается установление
статистической связи между функцией zи вероятностными переменнымиx,
y, tи др., т. е. связи вида![]()
Если диапазон изменения значений аргументов невелик, то в практике пользуются линейным уравнением множественной корреляции (регрессии)
![]() . (4.8)
. (4.8)
Если исследователь
имеет основание считать, что связь
функции с каким-либо аргументом
нелинейная, то в зависимость (14.8) включают
дополнительные члены вида
![]() и т.д.
и т.д.
Для определения
параметров
![]() используется упрощенный графоаналитический
метод, базирующийся на последовательном
определении статистических связей
используется упрощенный графоаналитический
метод, базирующийся на последовательном
определении статистических связей![]() и т.д.
и т.д.
Алгоритм определения параметров множественной линейной корреляции представлен ниже. Его удобнее всего продемонстрировать на примере.
Пример.Пусть
требуется определить статистическую
зависимость![]() ,
где значения случайных величин
,
где значения случайных величин![]() заданы таблицей 14.8.
заданы таблицей 14.8.
Таблица 4.8 –
Значения параметров
![]()
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
xi |
0.8 |
1,2 |
1,3 |
1,5 |
1,9 |
2 |
2,2 |
2,5 |
3 |
3,4 |
|
yi |
0,1 |
0,7 |
0,4 |
1,2 |
2 |
1,6 |
2 |
0,5 |
1,7 |
1,8 |
|
zi |
2,4 |
3 |
3,5 |
2,5 |
3 |
3,2 |
3,6 |
5,4 |
5,1 |
5,9 |
Зависимость
![]() будем искать в виде
будем искать в виде
![]() . (4.9)
. (4.9)
Алгоритм
определения коэффициентов
![]() состоит в следующем.
состоит в следующем.
1. Определяются
средние значения
![]() .
Они равны, соответственно,
.
Они равны, соответственно,![]() .
.
2. Переменные x, y, zцентрируются, т.е. осуществляется переход к новым переменным, имеющим нулевые средние значения. Для этого зависимость (14.9) представляется в виде системы уравнений
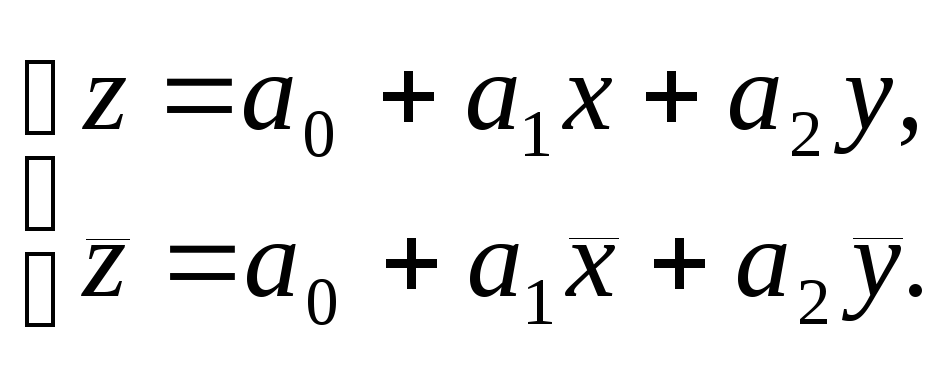
Отсюда следует, что
![]() . (4.10)
. (4.10)
![]() α
α![]()
3. Переходим к новым
переменным
![]() (смотри подстрочные буквы в формуле
(4.10.)) и строим новую таблицу значений
(смотри подстрочные буквы в формуле
(4.10.)) и строим новую таблицу значений![]() для того, чтобы найти частную зависимость
для того, чтобы найти частную зависимость![]() .
.
Таблица 4.9 –
Значения параметров
![]()
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
αi |
-1,2 |
-0,8 |
-0,7 |
-0,5 |
-0,1 |
0 |
0,2 |
0,5 |
1 |
1,4 |
|
γi |
-1,4 |
-0,8 |
-0,3 |
-1,3 |
-0,8 |
-0,6 |
-0,2 |
1,6 |
1,3 |
2,1 |
Зависимость
![]() будет центрирована, т.к. коэффициент
будет центрирована, т.к. коэффициент![]() – исключен, а средние значенияaиb
равны нулю. Получаем следующую
совокупность точек на графике
– исключен, а средние значенияaиb
равны нулю. Получаем следующую
совокупность точек на графике![]() – рисунок 4.8.
– рисунок 4.8.
4. Строим «облако
рассеивания» параметров
![]() и прямую, проходящую через начало
координат. Графически определяем
параметр
и прямую, проходящую через начало
координат. Графически определяем
параметр![]() в зависимости (4.10). Он равен
в зависимости (4.10). Он равен![]() – рисунок 4.8.
– рисунок 4.8.
5. Теперь коэффициент
![]() известен, поэтому построим следующую
зависимость преобразованной функцииz для второй
переменной:
известен, поэтому построим следующую
зависимость преобразованной функцииz для второй
переменной:
![]() ,
,
![]()
![]()
т.е. зависимость
![]() – см. нижние символы в предыдущей
формуле. Исходные данные для ее построения
приведены в таблице 4.10.
– см. нижние символы в предыдущей
формуле. Исходные данные для ее построения
приведены в таблице 4.10.
Таблица 4.10 –
Значения параметров![]()
|
I |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
βi |
-1,1 |
-0,5 |
-0,8 |
0 |
0,8 |
0,4 |
0,8 |
-0,7 |
0,5 |
0,6 |
|
di |
0,6 |
0,53 |
0,86 |
-0,47 |
-0,63 |
-0,61 |
-0,53 |
0,77 |
-0,37 |
-0,23 |
В
результате обработки данных, получаем
следующую совокупность точек
![]() и «облако рассеяния» (рисунок 14.9).
и «облако рассеяния» (рисунок 14.9).

Рисунок
4.8 – Зависимость![]()
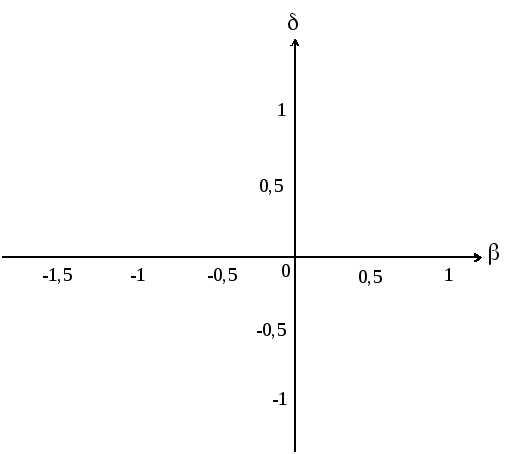
Рисунок
4.9 – Зависимость![]()
Расчетами,
аналогичными предыдущим, находим
![]() .
Таким образом, предварительно получаем
.
Таким образом, предварительно получаем![]() .
Для определения коэффициента
.
Для определения коэффициента![]() вычислим
вычислим
![]() .
.
Здесь под знаком суммы находятся значения а0i,(см. таблицу).
Таблица 4.11 –
Значения ![]()
|
I |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
a0i |
1,16 |
1,59 |
1,66 |
1,02 |
1,54 |
1,29 |
1,8 |
1,83 |
1,55 |
1,75 |
Получаем
![]() .
Итак, приближенно
.
Итак, приближенно
![]() .
(4.11)
.
(4.11)
Для множественной
корреляции могут быть рассчитаны частные
![]() иобщийr0
коэффициенты корреляции,
характеризующие тесноту связи функцииzс отдельными
аргументами и с их совокупностью.
Значения частных коэффициентов корреляции
(близость их по абсолютной величине к
единице) говорит о возможности выявления
парной корреляционной зависимости
между функцией и одним из аргументов.
Расчет их осуществляется по формулам,
подобным (4.3). Например,
иобщийr0
коэффициенты корреляции,
характеризующие тесноту связи функцииzс отдельными
аргументами и с их совокупностью.
Значения частных коэффициентов корреляции
(близость их по абсолютной величине к
единице) говорит о возможности выявления
парной корреляционной зависимости
между функцией и одним из аргументов.
Расчет их осуществляется по формулам,
подобным (4.3). Например,
![]() ,
,
где
![]() – средние значения соответствующих
величин;
– средние значения соответствующих
величин;
![]() –среднее значение
произведений
–среднее значение
произведений
![]() ;
;
![]() –среднеквадратичные
отклонения соответствующих величин от
среднего значения.
–среднеквадратичные
отклонения соответствующих величин от
среднего значения.
Формула для расчета общего коэффициента множественной корреляции r0 имеет вид
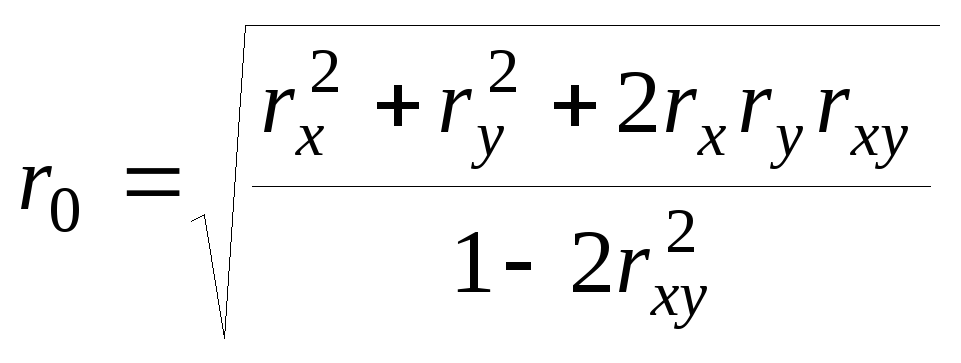 ,
(4.12)
,
(4.12)
где rxy – условный коэффициент корреляции между аргументамих, у:
Определим частные
и общий коэффициенты корреляции
установленной зависимости (4.11). Для
этого используем значения
![]() и вычислим
и вычислим
![]() ,
,![]() ,
,
![]() ,
,
![]() .По формулам, аналогичным (4.3) и далее,
получаем
.По формулам, аналогичным (4.3) и далее,
получаем![]() ;
;![]() ;
;![]() ;
;![]()
Далее находим
![]() ,
,
![]() ,
,![]() .
.
Таким образом, корреляционная связь между функцией z и аргументамиx,yсуществует, однако, парной корреляционной зависимости между функцией и одним из аргументов не прослеживается. К учету нужно принимать обе переменных.
Общий коэффициент корреляции равен
![]() .
.
Значит,
имеется средняя статистическая связь
между переменными в зависимости
![]() .
.
Самостоятельная задача. Для исходных данных (таблица 4.12) найти множественную корреляционную зависимость вида (4.9) и вычислить общий коэффициент корреляции.
Таблица 4.12 –
Значения параметров
![]()
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
xi |
0,4 |
3,5 |
2,4 |
0,8 |
1,0 |
5,0 |
3,1 |
2,5 |
1,5 |
0,2 |
|
yi |
2,4 |
3,8 |
1,2 |
1,1 |
0,6 |
4,2 |
3,1 |
1,8 |
2,0 |
2,8 |
|
zi |
5,1 |
4,3 |
0,7 |
1,7 |
1,0 |
3,6 |
3,5 |
1,8 |
1,2 |
6,2 |
