6, 4, 5, 7, 6, 4, 8, 6, 8, 9. 3, 2, 0, 4, 4, 3, 4, 1, 5, 7.

в) 3, 6, 7, 5, 3, 7, 4, 6, 8, 9, 6, 7. г) 7, 7, 4, 6, 1, 2, 5, 2, 3, 4, 5, 3.

3, 6, 3, 4, 6, 9, 4, 9, 6, 5. 3, 4, 6, 4, 2, 3, 6, 3, 4, 1.

Самостоятельная работа №3

Выполнить самостоятельную работу (таблица 3.12).

Таблица 3.12

№ по списку	1	2	3	4	5	6	7	8	9	10	11	12
Вопросы, задачи	1 5а 6 7 8б	2 5в 6 7 8а	3 5б 6 7 8г	2 5г 6 7 8в	4 5д 6 7 8а	2 5а 6 7 8б	1 5д 6 7 8в	2 5г 6 7 8г	4 5е 6 7 8г	2 5в 6 7 8б	3 5б 6 7 8в	2 5е 6 7 8а

Продолжение таблицы 3.12

№ по списку	13	14	15	16	17	18	19	20	21	22	23	24
Вопросы, задачи	1 5а 6 7 8а	2 5б 6 7 8б	1 5в 6 7 8в	2 5г 6 7 8г	3 5д 6 7 8б	4 5г 6 7 8в	3 5а 6 7 8г	4 5б 6 7 8а	3 5в 6 7 8а	4 5г 6 7 8б	1 5д 6 7 8в	2 5е 6 7 8г

4 Статистические зависимости и связи

4.1 Подбор эмпирических формул (парная корреляция)

В процессе исследования различных вероятностных зависимостей часто получают статистические ряды измерений двух величин, когда каждому значению аргумента соответствуют значения функций При этом требуется установить между ними функциональную связь.

На основе обработки экспериментальных данных можно подобрать алгебраические выражения для этой функции в виде.Они называютсяэмпирическими формулами.

Если значения заранее заданы, а значения – случайные, то эта зависимость называетсярегрессионной. Если случайными являются и аргументы , то зависимость называетсякорреляционной.

Подбираемые эмпирические формулы должны быть по возможности простыми. Их подбор состоит из двух этапов.

Вначале результаты измерений наносят на сетку прямоугольных координат, проводят через область экспериментальных точек плавную кривую и ориентировочно выбирают вид эмпирической формулы (функции). Затем подбирают параметры функции, которые наилучшим образом соответствовали бы принятой зависимости.

Подбор формул необходимо начинать с самых простых. Так, например, результаты измерений параметров многих зависимостей аппроксимируются прямыми вида

, (4.1)

где – постоянные коэффициенты.

Последовательность определения коэффициентов в эмпирических формулах зависит от их вида, т. е. линейные они или нелинейные. Вычисление коэффициентов базируется на методе наименьших квадратов. Суть его заключается в том, что прямая (или кривая) с вычисленными по этому методу коэффициентами располагается между экспериментальными точками так, что сумма квадратов расстояний от этих точек до прямой (кривой) будет наименьшей из всех возможных.

Для приближенного построения, например, прямолинейной зависимости можно использовать упрощенный графический метод. Его суть заключается в том, что на сетке прямоугольных координат, куда нанесены точки (), проводится прямая, удовлетворяющая следующим условиям:

- она проходит через точку, которая имеет координаты () – средние значения для аргумента и функции;

- прямая располагается вдоль “облака” значений ();

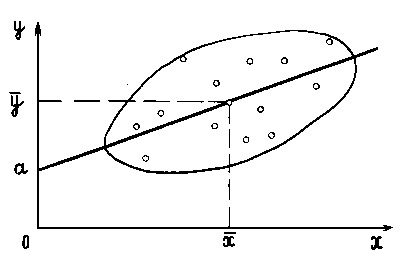
- площади частей “облака”, расположенных сверху и снизу от прямой примерно одинаковы, т. е. примерно одинаково число точек – рисунок 4.1.

Рисунок 4.1 – Иллюстрация графического метода построения

прямолинейной корреляционной зависимости

Замечание.Если форма "облака" криволинейна, то статистическая зависимость также будет криволинейной. Определение параметров кривой рассматривается ниже.

Опыт показывает, что различие в значениях коэффициентов a, bпри использовании графического метода составляет не более 5–10 % по сравнению с классическимметодом наименьших квадратов. Значения коэффициентовa, bлинейной зависимости (4.1)определяют путем решения системы уравнений

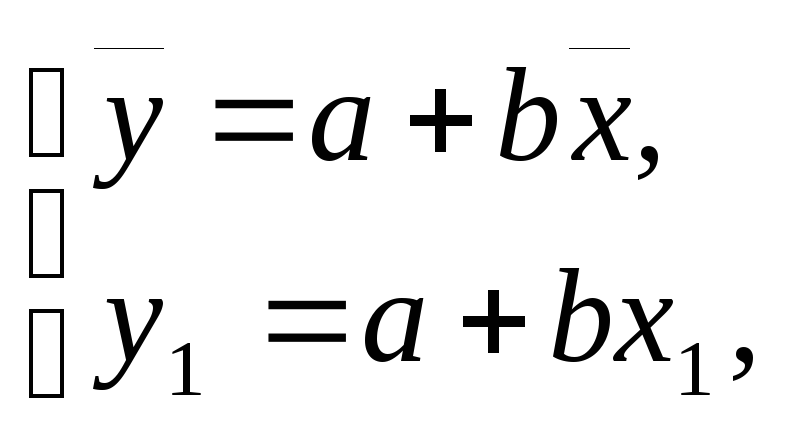(4.2)

где (х₁, у₁) –координаты любой, достаточно удаленной от () точки, лежащей на прямой.

Количественным показателем тесноты статистической связи между переменными x, yдля прямолинейной зависимости являетсякоэффициент парной корреляцииrв случае, если зависимость корреляционная икорреляционное отношение, если зависимость регрессионная. Чем ближе абсолютная величинаrк единице, тем теснее связь, т. е. адекватнее описание статистической зависимости этой формулой.

Если в прямолинейной зависимости коэффициент bположителен, т.е. функция возрастает, тоr >0, еслиbотрицателен, т.е. имеем убывающую функцию, то коэффициент корреляции будет меньше нуля; однако он всегда находится в диапазоне 0£½r½£1. Для большинства статистических задачтеснота связи считается удовлетворительной, когдаr по абсолютной величине превышает 0,80.

Коэффициент корреляции или корреляционное отношение рассчитываются по формуле

= , (4.3)

где s_x,s_y– среднеквадратичные отклонения соответственно для, ; они рассчитываются по формулам

s_x;s_y. (4.4)

Здесь n– число точек, по которым строится зависимость.

Величина () рассчитывается по формуле

.

Это среднее значение произведенийслучайных величин статистической выборки.

Задача 1.В результате измерений получены следующие статистические значения (таблица 4.1).

Таблица 4.1 – Статистические данные к построению

регрессионной зависимости

	1	2	3	4	5	6	7	8
	0,4	0,5	0,6	1,0	1,8	1,6	2,3	3,0

Требуется подобрать коэффициенты a, b прямолинейной регрессионной зависимости, найти корреляционное отношение и построить зависимостьу(х).

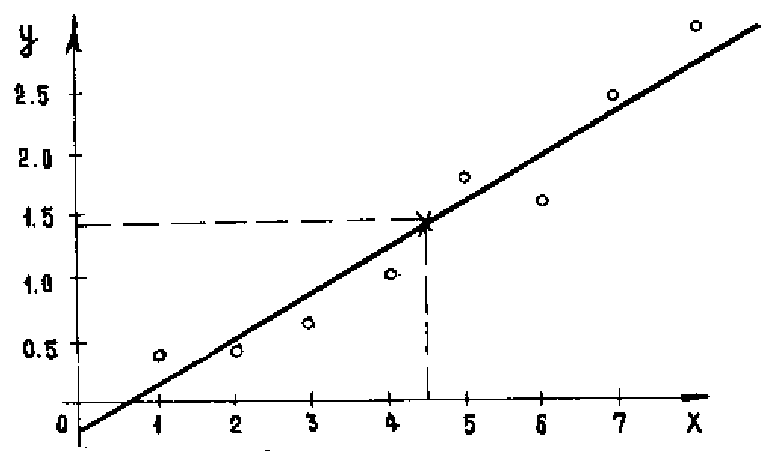
Решение. Воспользуемся упрощенным графическим методом. Для этого вычислим

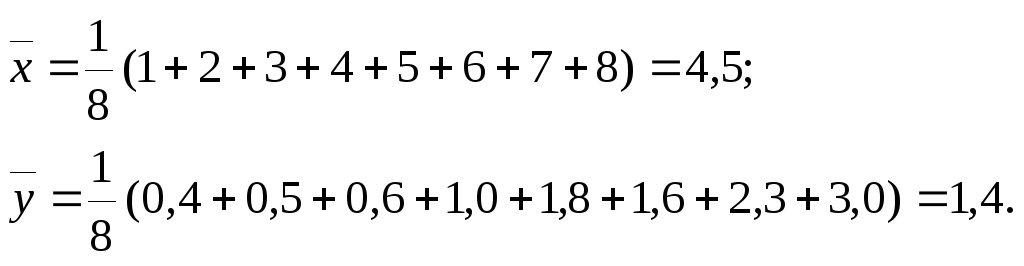
Получаем точку (4,5; 1,4), через которую должна проходить прямая. Проводим эту прямую, используя графический метод построения регрессионных зависимостей. Для этого приближенно построим "облако" и вдоль него расположим прямую, проходящую через точку () – рисунок 4.2.

Рисунок 4.2 – Регрессионная прямая

Коэффициенты a, bуравнения прямой можно получить, решая систему линейных уравнений для средней и любой достаточно удаленных от средней и лежащей в облаке рассеяния точки; например, для точки () и точки с координатами (2;0,5):

Получаем a=-0,22; b=0,36.

Окончательная зависимость принимает вид

Коэффициент корреляции определяем по формуле (4.3). Для этого по формулам (14.4) находим s_xs_y. Далее вычисляем .

Тогда получаем

При использовании метода наименьших квадратов коэффициенты aиbв зависимости (4.1) определяются по формулам

, .

Получаем точные значения

, .

Графический метод удобнее в случаях, когда коэффициент корреляции определять не обязательно (например, наличие статистической связи между переменными x,yявляется визуально очевидным).

Самостоятельная задача 1.Установить статистическую зависимость весаРот ростаhдля выборочной группы из 20 чел. При этом для пары значений (h_i, Р_i) первое значение задается из условийзадачи 1, а второе – из условийсамостоятельной задачи подраздела 3.2. Таким образом, имеем следующую таблицу значений выборочных величин.

Таблица 4.2 – Статистические данные для построения зависимости P(h)

hi, см	165	158	170	180	163	171	168	172	162	177
Рi, кг	60	51	66	74	57	67	62	70	60	76

hi, см	175	166	169	179	164	170	169	167	175	181
Рi, кг	73	63	67	66	59	69	64	63	72	77

Если статистическая (эмпирическая) функция не укладывается в линейный вид, т.е. "облако" является существенно криволинейным, используют так называемый метод выравнивания. Он заключается в замене системы координат, при которой функция принимает вид прямой. Для преобразования некоторой кривой в прямую линию вводят новые переменные

;. (4.6)

В преобразованной системе и на плоскости переменные X и Yдолжны быть связаны линейной зависимостью Значения коэффициентоваиbможно вычислить на основе решения системы уравнений (4.2). Далее, по экспериментальным точкам, координаты которых преобразованы, строят прямую, а затем восстанавливают завимость исходного вида. Наиболее распространенные кривые представлены на рисунке 4.3.

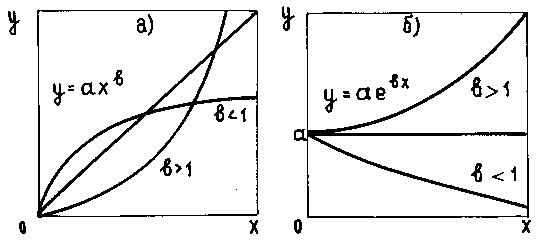
Рисунок 4.3 – Кривые для реализации метода Выравнивания

Приведем некоторые примеры.

Пусть предполагаемая эмпирическая зависимость имеет вид , что определяется графически (рисунок 4.3а). Прологарифмируем обе части этого соотношения. Получимln y =ln ax^b =ln a + b ln x. Тогда в новых координатахX=lnx;Y=lny получаем прямую

, где

Если зависимость имеет вид (рисунок 4.3б), то после логарифмирования находимln y = ln a + b x,и в координатахX=x;Y=ln yполучаем прямую

, где X=x,

Задача 2. Пусть в результате измерений получены следующие значения, (таблица 4.3).

Таблица 4.3 – Исходные статистические данные

Xi	1	2	3	4	5	6	7	8
Yi	0,4	0,5	0,6	1,0	1,8	2,6	2,4	4,6

Требуется подобрать коэффициенты a, bрегрессионной зависимости вида, найти корреляционное отношение и построить график исходной зависимостиу(х).

Решение. Перейдем к новой системе координатX=x, Y=lny. где зависимость у(х) превращается в прямую. Новая таблица значенийХ_i, Y_i будет следующей.

Таблица 4.4 – Выровненные статистические данные

	1	2	3	4	5	6	7	8
	-0,92	-0,69	-0,51	0	0,59	0,96	0,88	1,53

Вычисляем средние значения величин X,Y. Получаем . В системе координат (X0Y) это будет точка (4,5; 0,25), через которую должна проходить прямаяY=c+bX.Проведем эту прямую (рисунок 4.4), используя графический метод. Коэффициентыc, b найдём из системы уравнений

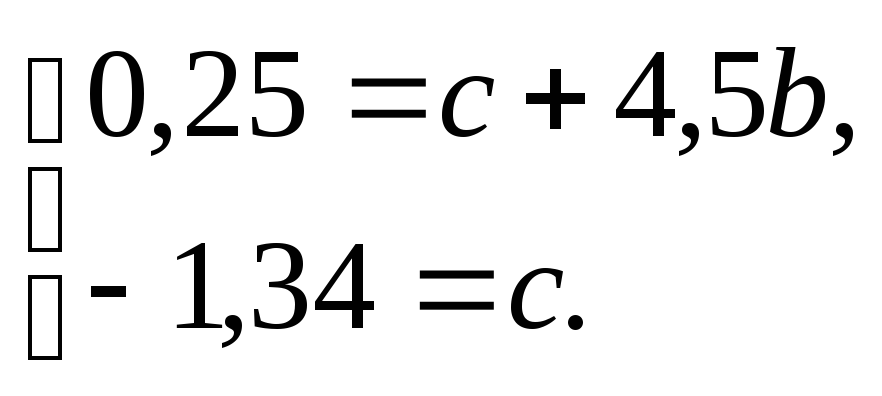
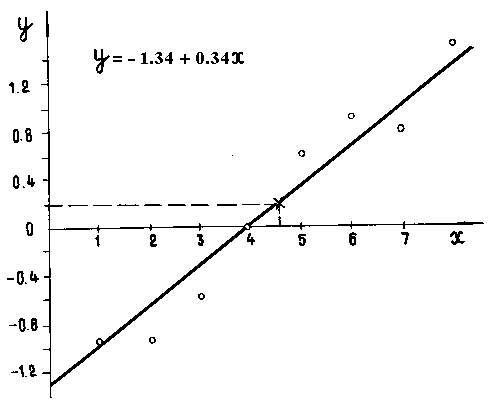
Получаем b=0,35, c =–1,34. Следовательно, график функции описывается приведенной ниже прямой (см. рисунок 4.4).

Рисунок 4.4 – Спрямленная корреляционная зависимость

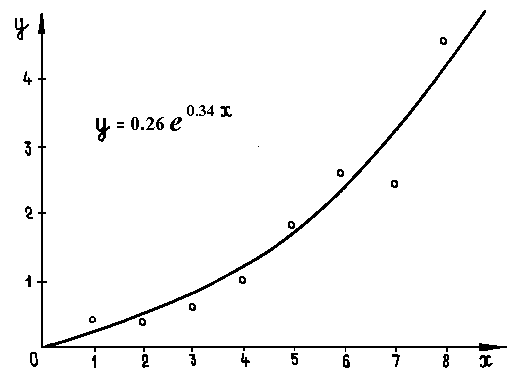
Учитывая, что ln a=–1,34, получаем искомую зависимость. Вид установленной статистической зависимости, учитывающий, что величинас равна –1,34 иe^-1,34 = 0,26, приведен на рисунке4.5.

Для расчета корреляционного отношения rвоспользуемся данными, приведенными в таблице 4.4, и формулой (4.3). Находим,s_xs_y, Тогда получаем

Рисунок 4.5 – Исходная зависимость

Самостоятельная задача 2. Найти статистическую зависимость видаy = ax^b, определить корреляционное отношение и построить график. Выборочные значениях_i, y_i приведены в таблице 4.5.

Таблица 4.5 – Исходные статистические данные

xi	0,2	0,5	1	1,5	2	2,5	3	4	4,5	5
yi	0,5	0,7	1,2	1,5	1,8	2,0	2,2	2,0	2,2	2,5

Самостоятельная задача 3. Найти статистическую зависимость видаy = ae^bx, определить корреляционное отношение и построить график. Выборочные значениях_i, y_i приведены в таблице 14.6.

Таблица 4.6 – Исходные статистические данные

xi	0,2	0,5	1	1,5	2	2,5	3	4	4,5	5
yi	0,5	0,7	0,7	1	1,5	1,7	2	3	5	7