3.2 Выборочный метод

Изучение множества сходных объектов может проводиться как по качественному, так и по количественному признакам. Например, если анализируется возрастной состав работающих на предприятии, то качественным признаком может быть их совершеннолетие или несовершеннолетие, а количественным – возраст работающих. Анализируя их возраст, можно использовать два подхода:

1)определять возраст всех объектов исследования;

2)определять возраст объектов только для отдельной представительной группы и из этого делать выводы, касающиеся всех объектов исследований.

Очевидно, что первый подход нерационален. При втором подходе множество случайным образом отобранных объектов называется выборочной совокупностьюили простовыборкой.Все множество объектов, подлежащих исследованию, называетсягенеральной совокупностью. Число объектов выборочной совокупности называютобъемом выборки. Обычно генеральная совокупность содержит конечное множество объектов. Оно, как правило, велико, поэтому при теоретических выводах объем генеральной совокупности часто предполагается бесконечным.

Вариационный ряд и эмпирическая функция распределения.Пусть для изучения количественного признакаХиз генеральной совокупности отобранопобъектов, характеризуемых статистическими даннымих₁,х₂,…, х_n.Наблюдаемые значениях_iназываютсявариантами. Если их расположить в порядке возрастания, то полученная последовательность образуетвариационный ряд. Вариационные ряды удобны для статистического оценивания функции распределения случайной величины.

Обозначим k – число значений случайной величины, меньших, где–члены вариационного ряда. Зная общее число членов рядап,можно построить функцию

,

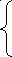
(3.1)

, (

Эта функция называется эмпирической функцией распределенияслучайной величиных.Она и определяет приближенно функцию распределенияF(х). В 1933г. советским математиком В.И. Гливенко доказанаосновная теорема математической статистики,которая доказывает, что при больших значенияхп эмпирической функцией распределения приближается к теоретической:F_n(x)®F(x) при n®¥.

Кроме эмпирической функции распределения для исследований полезно построить гистограмму f_п(х), являющуюсяэмпирической плотностью вероятностей. Для этого задаются интервалы ∆х_i, далее определяются количества значений (частот) – ∆n_i(x), попавших в каждый из интервалов.Затем строится столбчатая функция, высота столбцов которой в отдельных интервалахравна ∆n_i(x)/n∆x=f_n(x).Общая площадь под гистограммой равна 1.

Задача 1.Построить гистограмму и эмпирическую функцию распределения роста выборочной группы изN= 20 чел. для следующей выборки (рост, см):

165, 158, 170, 180, 163, 171, 168, 174, 162, 177,

175, 166, 169, 179, 164, 170, 169, 167, 175, 181.

Решение.Расположим значения выборки в порядке возрастания, т.е. в видевариационного ряда:

158, 162, 163, 164, 165, 166, 167, 168, 169,169,

170, 170, 171, 174, 175, 175, 177, 179, 180, 181.

Изменения роста выборочной группы находится в диапазоне от 158 до 181 см, т.е. х_max– x_min= 181–158 = 23 см.

Количество наблюдений при статистических исследованиях обычно бывает достаточно большим. Теория и практика статистических расчетов показывает, что группировка данных по 8–12 интервалам, в каждый из которых попадает не более 10–15% значений x_i,оказывается достаточной для выявления свойств распределений и надежного вычисления характеристик случайных величин. При малых выборах (n<30) число интервалов гистограммыmследует принимать равным 5–7. При больших выборках (n >30) число интервалов можно рассчитывать по формуле

.

Число интервалов должно быть удобным для построения гистограммы. Для предыдущей задачи, при длине интервалов 4 см., получаем семь интервалов: 156 – 160; 160 – 164; …; 180 – 184 см.

Гистограмма распределения и диаграмма представлены на рисунке 3.1. В диаграмме на оси ординат откладывается число значений, попавших в i-ый интервал, на гистограмме – значения n_i(x)/n∆x=f(x).

В интервал (х_i-1; x_i) помещают значения х, которые меньше x_i:

- т.е. в первом интервале n₁ = 1 (158 см);

- во втором – n₂ = 2 (162, 163);

- в третьем – n₃ = 4 (164, 165, 166, 167) и т.д.,

в седьмом интервале число значений n₇ = 2 (180, 181).

Общая площадь гистограммы распределения, согласно построению, равна 1,0

Таким образом, она является аналогом плотности распределения случайной величины х илиэмпирической плотностью распределения.

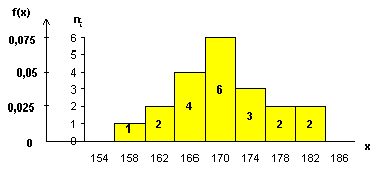
Рисунок 3.1 – Гистограмма и диаграмма распределения

На рисунке 3.2 для этой гистограммы построена эмпирическая функция распределения F_n (x). На этом примере видны основные особенности эмпирической функции распределения. Как и теоретическая, она не убывает и значения ее не выходят из интервала [0; I].

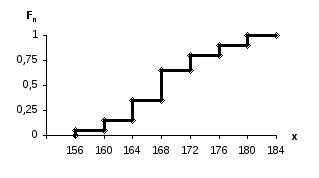
Рисунок 3.2 – Эмпирическая функция распределения

Самостоятельная задача 1.Построить гистограмму и эмпирическую функцию распределения веса выборочной группы изN=20 чел. для следующей выборки (вес, кг):

60, 51, 66, 74, 58, 67, 62, 68, 61, 76,

68, 63, 67, 74, 59, 69, 64, 63, 72, 65. (3.2)