В решение данной задачи мы добавили еще значение вероятностей количества бракованных деталей в диапазоне от 0 до 7 и представили график функции распределения и график многоугольника распределения вероятностей.
Задание для самостоятельной работы
На завод прибыла партия деталей в количестве n шт. Вероятность того, что наудачу выбранная деталь окажется бракованной, равна p. Какова вероятность того, что среди прибывших деталей число бракованных будет в диапазоне от k1 до k2 ? Значения па-
раметров n, p, k1 и k2 заданы в таблице.
№ |
p |
n |
k1 |
k2 |
№ |
p |
n |
k1 |
k2 |
1. |
0,001 |
1000 |
0 |
5 |
16. |
0,001 |
4000 |
3 |
10 |
2. |
0,002 |
2000 |
1 |
5 |
17. |
0,008 |
1000 |
12 |
900 |
3. |
0,003 |
3000 |
8 |
12 |
18. |
0,009 |
2000 |
2 |
800 |
4. |
0,004 |
2000 |
4 |
8 |
19. |
0,001 |
3000 |
0 |
6 |
5. |
0,005 |
1000 |
5 |
9 |
20. |
0,002 |
4000 |
4 |
12 |
6. |
0,006 |
1500 |
7 |
10 |
21. |
0,003 |
1000 |
3 |
6 |
7. |
0,007 |
1100 |
6 |
10 |
22. |
0,004 |
2000 |
8 |
20 |
8. |
0,008 |
900 |
5 |
8 |
23. |
0,005 |
3000 |
15 |
20 |
9. |
0,009 |
1000 |
0 |
12 |
24. |
0,006 |
4000 |
30 |
40 |
10. |
0,001 |
5000 |
2 |
8 |
25. |
0,007 |
1000 |
7 |
20 |
11. |
0,002 |
3000 |
4 |
9 |
26. |
0,008 |
2000 |
2 |
16 |
12. |
0,003 |
1600 |
4 |
20 |
27. |
0,009 |
3000 |
22 |
27 |
13. |
0,004 |
1000 |
3 |
9 |
28. |
0,001 |
4000 |
4 |
40 |
14. |
0,005 |
2000 |
0 |
3 |
29. |
0,002 |
5000 |
0 |
10 |
15. |
0,006 |
1500 |
5 |
15 |
30. |
0,003 |
6000 |
12 |
18 |
6.2. Непрерывная случайная величина
Если возможные значения случайной величины образуют некоторый непрерывный конечный или бесконечный интервал [a;b], то такая случайная величина называется непрерывной слу-
чайной величиной. Непрерывная случайная величина задается
функцией плотности распределения вероятностей ϕ(x) . При
109
этом функция плотности должна быть неотрицательна и удовлетворять условию
∞ |
|
∫ ϕ(x)dx =1. |
(6.13) |
−∞
Таким образом, площадь между осью абсцисс и графиком функции плотности равна 1.
При этом функция распределения задается формулой:
F(x) = ∫x |
ϕ(t)dt . |
(6.14) |
−∞ |
|
|
Для вычисления вероятности того, что случайная величина ξ принимает значение на некотором интервале [x1, x2 ), применяется следующая формула:
x2 |
|
|
P(x1 ≤ξ < x2 ) = ∫ |
ϕ(t)dt. |
(6.15) |
x1 |
|
|
Зная функцию распределения, можно найти функцию плотности по следующей формуле
ϕ(x) = F (x). |
(6.16) |
′ |
|
Математическим ожиданием непрерывной случайной величины ξ с плотностью распределения ϕ(x) называется
+∞ |
|
M (ξ) = ∫ xϕ(x)dx. |
(6.17) |
−∞
Определение дисперсии непрерывной случайной величины определению дисперсии дискретной случайной величины.
D(ξ) = M (ξ − M (ξ))2 . |
(6.18) |
Дисперсию непрерывной случайной величины можно вычислять по формулам:
D(ξ) = +∞∫(x − M (ξ))2 ϕ(x)dx, |
(6.19) |
−∞ |
|
или D(ξ) = +∞∫ x2ϕ(x)dx −(M (ξ))2 = M (ξ2 ) −(M (ξ))2 . |
(6.20) |
−∞ |
|
Пример. Плотность распределения непрерывной случайной величины задана следующим образом:
110
0, |
если |
x < 0; |
|
если |
0 ≤ x ≤ 5; |
ϕ(x) = a (5x − x2 ), |
||
|
если |
x > 5. |
0, |
Определите неизвестную константу a и найдите вероятность того, что случайная величина ξ примет значение, удовлетво-
ряющее неравенствам −1 ≤ξ ≤ 2. Найдите математическое ожи-
дание, дисперсию, среднее квадратическое отклонение и функцию распределения заданной случайной величины. Постройте график функции распределения и функции плотности заданной непрерывной случайной величины.
Начало программы.
Функция плотности
φ(x,a) := |
a (5 x − x2 ) if 0 ≤ x ≤ 5 |
|||
|
|
0 |
otherwise |
|
|
1 |
|
|
|
a := |
|
a = 0.048. |
Вычисление неизвестной величины a. |
|
5 |
|
|||
|
∫φ(x,1)dx |
|
|
|
|
0 |
|
|
|
Проверка правильности задания функции плотности и вычисление искомой вероятности P.
∞ |
β |
∫φ(x,a)dx =1 α := −1 β := 2 |
P := ∫φ(x,a)dx P = 0.352 |
−∞ |
α |
Вычисление числовых характеристик случайной величины ξ .
∞
M := ∫ x φ(x,a)dx M = 2.5.
−∞
∞
D := ∫ (x − M )2 φ(x,a)dx D =1.25 σ := D σ =1.118.
−∞
Задание функции распределения F(x)
x
F(x) := ∫ φ(t,a)dt
−∞
111
Конец программы.
Рассмотрим теперь наиболее распространенные распределения непрерывных случайных величин: равномерное, экспоненциальное и нормальное распределения. Для каждого из этих распределений в Mathcad встроены по две функции для функции плотности (начинается на букву d) и функции распределения (начинается на букву p).
Равномерное распределение. Распределение непрерывной случайной величиныξ называется равномерным на отрезка [a; b],
если плотность распределения ϕ(x) и функция распределения F(x) имеют следующий вид:
0
ϕ(x) = 1
−b a
при x [a;b],
при x [a;b],
0 −
F(x) = x a
b −a1
при x ≤ a,
при x (a;b], (6.21)
при x > b.
В Mathcad значения функции плотности распределения и функции распределения для равномерно распределенной случайной величины на отрезке [a;b] задаются при помощи встроенных
функций dunif(x,a,b) и punif(x,a,b).
Пример. Случайная величина ξ имеет равномерное распределение на отрезке [−1; 4]. Построить графики функции плотно-
сти и функции распределения, а также найти вероятность того, что случайная величина ξ примет значения в диапазоне от 0 до 5.
Решение:
a :=1 b := 4 F(x) = punif (x,a,b) F(5) − F(0) = 0.8.
112
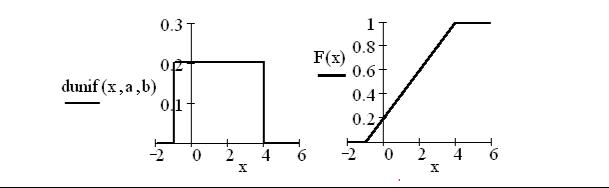
На левом графике изображена функция плотности, а на правом – функция распределения заданной равномерной случайной величины. Значение искомой вероятности равно 0.8.
Экспоненциальное распределение. Распределение непре-
рывной случайной величиныξ называется экспоненциальным (показательным), если плотность распределения имеет вид:
|
|
−λx |
при |
x ≥ 0, |
|
λe |
|
(6.22) |
|||
ϕ(x) = |
0 |
при |
x < 0, |
||
|
|
||||
|
|
|
|
|
|
где параметр распределения λ >0 .
Функция распределения экспоненциального закона имеет вид:
|
|
−e |
−λx |
при x ≥ 0, |
|
|
|
||||
F(x) = 1 |
|
|
|
(6.23) |
|||||||
|
0 |
|
|
при x < 0. |
|
|
|
||||
Как известно из [3], основные числовые характеристики рав- |
|||||||||||
ны: |
1 |
|
|
|
|
1 |
|
1 |
|
|
|
M (ξ) = |
; |
D(ξ) = |
; σ(ξ) = |
. |
(6.24) |
||||||
|
|
|
|||||||||
|
λ |
|
|
|
λ2 |
λ |
|
||||
В Mathcad значения функции плотности и функции распределения для экспоненциального закона c параметром λ вычисляются при помощи встроенных функций dexp(x,λ) и pexp(x,λ).
Пример. Непрерывная случайная величина имеет экспоненциальное распределение с параметром λ = 0,8. Построить функцию плотности и функцию распределения. Найти основные числовые характеристики случайной величины и вероятность того, что случайная величина ξ не превышает 2,4.
Программа на Mathcad выглядит следующим образом:
λ := 0.8 M := ∞∫ x d exp(x,λ)dx M =1.25 |
1 |
=1.25. |
|
λ |
|||
−∞ |
|
||
|
|
113
D := ∞∫(x − M )2 d exp(x,λ)dx |
D =1.562 |
1 |
=1.562. |
2 |
|||
−∞ |
P = 0.853. |
λ |
|
P := p exp(2.4,λ) − p exp(−∞,λ) |
|
|
|
Математическое ожидание и дисперсия вычислена двумя способами: по определению (6.2) и по формуле (6.3). Полученные результаты совпали. Вероятность того, что случайная величина ξ
не превышает значение 2,4, равна 0,853.
Нормальное распределение. Это распределение имеет большое теоретическое и прикладное значение в теории вероятностей и математической статистике. Случайная величина ξ имеет нор-
мальное распределение с параметрами a и σ , если ее плотность распределения имеет вид:
|
1 |
e− |
(x−a)2 |
|
|
ϕ(x) = |
2σ2 . |
(6.25) |
|||
2π σ |
|||||
|
|
|
|
Функция распределения нормального закона имеет вид:
|
1 |
x |
e− |
(t−a)2 |
|
|
F(x) = |
∫ |
2σ2 dt. |
(6.26) |
|||
2π σ |
||||||
|
−∞ |
|
|
|
||
|
|
|
|
|
Основные числовые характеристики нормально распределенной случайной величины (6.25) равны:
M (ξ) = a; D(ξ) =σ2; σ(ξ) =σ.
В Mathcad значения функции плотности распределения и функции распределения для нормального закона распределения вероятностей c параметрами a и σ вычисляются при помощи встроенных функций dnorm(x, a , σ ) и pnorm(x, a , σ ).
114
Пример. Случайная величина ξ подчиняется нормальному закону распределения вероятностей с параметрами a = 2,5;
σ =1,5.
I. Определить вероятности: 1) P(−1 <ξ <1); 2) P(| ξ −1|<σ);
3)P(| ξ −a |< kσ), k =1,2,3,4,5; 4) P(ξ > 3).
II. Нарисовать графики функции плотности и функции распределения заданной случайной величины.
III. Найти максимальное значение функции плотности. Приведем Mathcad-программу, решающую поставленную за-
дачу.
I. Искомые вероятности обозначим идентификаторами P1, P2, P3 и P4. При этом величина P3 является массивом из пяти элементов.
a := 2.5 σ :=1.5 P1 := pnorm( 1,a,σ ) − pnorm( −1,a,σ ) P1 =0.149. P2 := pnorm( 1 +σ,a,σ ) − pnorm( 1 −σ ,a,σ ) P2 =0.477.
Для ответа на третий вопрос используем ранжированный вектор k, принимающий значения 1, 2, 3, 4, 5.
ORIGIN :=1
k :=1..5 P3k := pnorm( a + k σ,a,σ ) − pnorm( a −k σ,a,σ ) P3T = (0.682689 0.9545 0.9973 0.999937 0.999999). P4 := pnorm( ∞,a,σ ) − pnorm( 3,a,σ ) P4 =0.369.
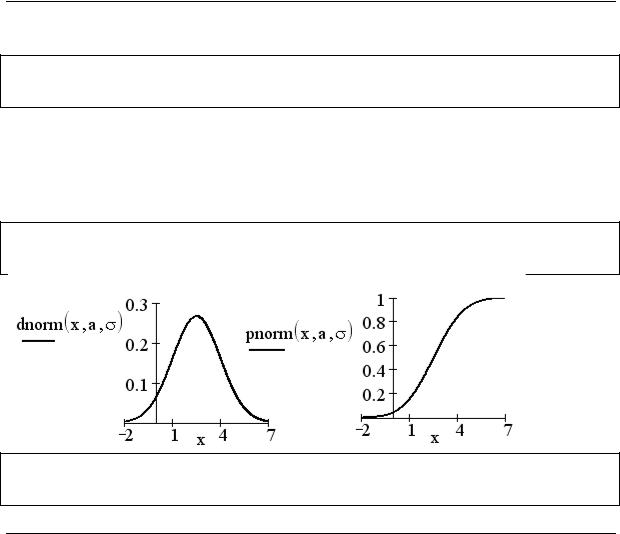
II. Построим теперь графики функции плотности dnorm и функции распределения pnorm.
III. Максимальное значение функции плотности достигается при x = a .
dnorm(a,a,σ) = 0.266.
115
Задание для самостоятельной работы
Случайная величина ξ подчиняется нормальному закону
распределения вероятностей с параметрами a и σ . I. Определить вероятности:
1) P(x1 <ξ < x2 ); 2) P(| ξ − x3 |<ε); 3) P(| ξ −a |< kσ), |
|
|||||||
k =1,2,3,4,5; |
4) P(ξ > x4 ). |
|
|
|
|
|||
II. Нарисовать графики функции плотности и функции рас- |
||||||||
пределения заданной случайной величины. |
|
|
||||||
III. |
Найти максимальное значение функции плотности. Па- |
|||||||
раметры a, σ, x1, x2 , x3 , x4 заданы в таблице. |
|
|
||||||
№ |
a |
|
σ |
x1 |
x2 |
x3 |
ε |
x4 |
1 |
–8 |
|
0,4 |
–8,7 |
–7,3 |
–7 |
0,4 |
–7 |
2 |
–7,5 |
|
0,5 |
–7 |
–6 |
–7,5 |
0,6 |
–8 |
3 |
–7 |
|
0,6 |
–9 |
–8 |
–8 |
0,7 |
–7 |
4 |
–6,5 |
|
0,7 |
–7 |
–5,5 |
–6 |
0,7 |
–6 |
5 |
–6 |
|
0,8 |
–6 |
–4 |
–6,5 |
0,6 |
–7 |
6 |
–5,5 |
|
0,9 |
–6 |
–5 |
–5 |
0,8 |
–6 |
7 |
–5 |
|
1 |
–7 |
–4 |
–5,5 |
1 |
–4 |
8 |
–4,5 |
|
1,1 |
–5 |
–2 |
–4 |
1,5 |
–5 |
9 |
–4 |
|
1,2 |
–4 |
–2 |
–3 |
1,2 |
–4 |
10 |
–3,5 |
|
1,3 |
–3 |
1 |
–4 |
1,5 |
–2 |
11 |
–2 |
|
1,4 |
–3 |
0 |
–3 |
1,5 |
–3 |
12 |
–1,5 |
|
1,5 |
–2 |
2 |
–1,2 |
0,9 |
–1 |
13 |
–1 |
|
1,6 |
–1,5 |
1 |
–2 |
1,5 |
–2 |
14 |
–0,5 |
|
1,7 |
0 |
4 |
–1 |
1,6 |
–1 |
15 |
0,5 |
|
0,4 |
0 |
1 |
0 |
0,5 |
0 |
16 |
1 |
|
0,5 |
1 |
2 |
0,5 |
0,4 |
2 |
17 |
1,5 |
|
0,6 |
2 |
3 |
2 |
0,5 |
2 |
18 |
2 |
|
0,7 |
2 |
3,5 |
2,5 |
0,8 |
1 |
19 |
2,5 |
|
0,8 |
2 |
3 |
2 |
0,9 |
2 |
20 |
3 |
|
0,9 |
2 |
4 |
2,5 |
0,7 |
2 |
21 |
3,5 |
|
1 |
2 |
4 |
4 |
1,2 |
2 |
22 |
4 |
|
1,1 |
3 |
5 |
6 |
1,5 |
3 |
23 |
4,5 |
|
1,2 |
4 |
6 |
3 |
1,2 |
5 |
24 |
5 |
|
1,3 |
4 |
7 |
4 |
1,5 |
6 |
25 |
5,5 |
|
1,4 |
4 |
6 |
5 |
2,5 |
7 |
116
26 |
6 |
1,5 |
7 |
10 |
7 |
2,2 |
4 |
27 |
6,5 |
1,6 |
6 |
9 |
4 |
2,1 |
6 |
28 |
7 |
1,7 |
8 |
12 |
8 |
1,5 |
8 |
29 |
7,5 |
0,4 |
7 |
11 |
7 |
1,8 |
7 |
30 |
8 |
0,5 |
8,5 |
12 |
3 |
3 |
9 |
В работе [3] представлены встроенные в Mathcad функции, применяемые в математической статистике, поэтому данный раздел в практикуме не рассматривается.
117