
- •Математический практикум с применением пакета Mathcad
- •Оглавление
- •1. Введение в Mathcad
- •1.1. Интерфейс Mathcad
- •1.1.1. Главное меню Mathcad
- •1.1.2. Панели инструментов
- •2. Задачи элементарной математики
- •2.2. Построение графиков функций
- •2.3. Решение алгебраических уравнений и систем
- •3. Задачи линейной алгебры
- •3.1. Основные сведения о матричных операциях
- •3.2. Решение типовых задач по линейной алгебре
- •4. Задачи математического анализа
- •4.1. Вычисление пределов числовых последовательностей и функций
- •4.2. Исследование сходимости и вычисление сумм рядов
- •4.3. Дифференцирование функций одной переменной
- •4.4. Интегрирование функции одной переменной
- •4.4.1. Неопределенные интегралы
- •4.4.2. Определенные интегралы
- •5.1. Решение задачи Коши
- •5.1.1. Решение задачи Коши методом Эйлера
- •5.1.2. Решение задачи Коши методом Рунге–Кутта второго порядка
- •5.1.3. Решение задачи Коши методом Рунге–Кутта четвертого порядка
- •5.1.4. Решение задачи Коши при помощи встроенных функций
- •5.2. Решение краевой задачи
- •6. Теории вероятностей и математическая статистика
- •6.1. Дискретные случайные величины
- •6.2. Непрерывная случайная величина
- •7. Программирование в Mathcad
- •Заключение
- •Предметный указатель
- •Список литературы

|
|
|
|
|
y(1) = 2 |
27 |
y′+ y 3 |
x2 |
= y3 cos3 2x +sin x |
[1; 10] |
|
|
|
|
|
|
y(1) = 2 |
28 |
y′+ y 3 |
x2 |
= cos 2x ln x |
[1; 9] |
|
|
|
|
|
|
y(1) = 3 |
29 |
y′+ y 3 |
x2 |
= y2 ln x sin x2 +sin 2x |
[1; 10] |
|
|
|
|
y(0) =1 |
||
30 |
y′+ xy cos 4x2 = e0,1x |
[0; 4] |
|||
5.1.4. Решение задачи Коши при помощи встроенных функций
Решение задачи Коши является стандартной, несложной, с вычислительной точки зрения, задачей. Естественно, что в пакете Mathcad встроены несколько функций, реализующих численное решение задачи Коши.
Наиболее удобным способом решения задачи Коши является вычислительный блок Given … Odesolve.
Этот блок реализует метод Рунге–Кутта четвертого порядка и имеет следующий общий вид:
Given
Уравнения и начальные данные задача Коши. y= odesolve(x,b,[N])
Здесь Given ключевое слово, указывающее на начало блока вычислений. Вместо уравнений и начальных данных необходимо задать в математическом виде дифференциальное уравнение n-го порядка или систему n уравнений первого порядка, представленных в нормальной форме. Вместо начальных данных необходимо задать n уравнений, определяющих значение искомой функции y(x) или ее производных в начальной точке a. b – правая граница области, на которой ищется решение задачи Коши. Необязательный параметр N определяет количество интервалов, на которые разбивается отрезок [a,b] при решении задачи методом Рунге–
Кутта.
Рассмотрим решение задачи (5.2) при помощи рассматриваемого вычислительного блока.
77
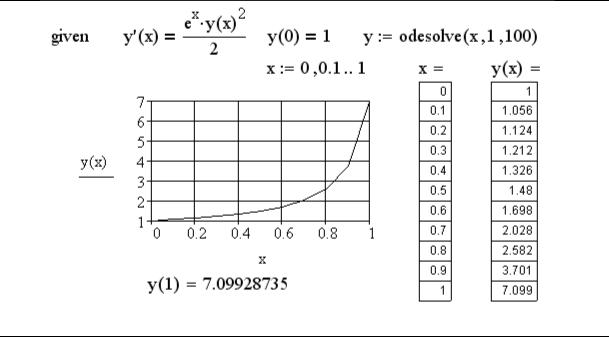
Начало программы.
Конец программы.
В первой строке данной программы получено решение задачи в виде функции y(x). Для ввода символа производной можно использовать комбинацию клавиш «Ctrl+F7». Для задания второй производной необходимо набрать эту комбинацию повторно. Символ = необходимо вводить при помощи комбинации двух клавиш «Ctrl+=». Во второй строке задана таблица переменной x и выведены значения таблиц x и у. Далее построен график полученного решения и выведено значение полученной функции в правой точке. Сравнивая полученное решение y(1) в вычислительном блоке Given/Odesolve с результатом, полученным по методу Рунге–Кутта при N=100, мы видим их полное совпадение. Читателям предлагается провести такое же сравнение для своих вариантов заданий.
Рассмотрим решение задачи о вынужденных колебаниях под воздействием внешней периодической возмущающей силы убывающей со временем амплитуды и сопротивления среды пропорциональной скорости колебания
y′′( t ) + 2by′( t ) +ω2 y( t ) = ae−0,01t sin μt, y( 0 ) = 0, y′( 0 ) = 0,t [ 0; T ].
Напишем программу для решения поставленной задачи.
78

Начало программы.
|
|
|
|
|
||||
ω := 0.1 |
μ := 0.2 |
a :=10 |
b := 2 |
T := 4000 |
||||
Given |
|
|
|
|
|
|
|
|
′′ |
′ |
|
2 |
y(t) = a e |
−0.01 t |
sin(μ t) |
||
y (t) + 2 |
b y (t) +ω |
|
|
|
||||
y(0) = 0 |
′ |
|
|
|
|
|
|
|
y (0) = 0 |
|
|
|
|
|
|
|
|
y := Odesolve(t,T ) |
|
y(T ) = 0.001 |
|
|
||||
Конец программы. |
|
|
|
|
|
|
|
|
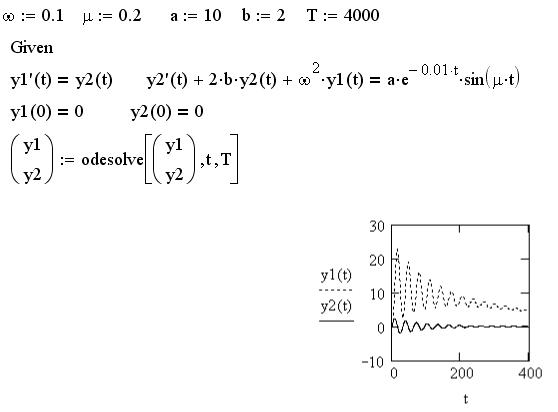
В качестве значений для параметров поставленной задачи ω, μ, a и b выбраны некоторые
произвольные числа. Можно исследовать поведения решения задачи Коши от каждого из этих параметров. Из графика полученной функции y(t) видно, что
вначале происходит затухание колебательных движений, при этом амплитуда колебательных движений со временем уменьшается, а затем при больших значениях t искомой функции стремит-
ся к нулю. y(T)=0,001.
Рассмотрим пример решения нормальной системы обыкновенных дифференциальных уравнений при помощи вычислительного блока Given/Odesolve. Пусть дана нормальная система трех дифференциальных уравнений с начальными условиями
t [t0,T].
dx |
= f (t,x, y,z), |
|||||
|
|
|
||||
1 |
||||||
dt |
|
|||||
|
|
|||||
|
dy |
|
|
= f2(t,x,y,z), |
||
|
|
|||||
dt |
|
|||||
dz |
= f2(t,x, y,z) |
|||||
|
|
|
||||
|
||||||
dt |
|
|||||
x(t0) =x0,
и начальные данные y(t0) =y0, t [t0,T].
z(t0) =x0
Программа для решения данной задачи на Mathcad c использованием вычислительного блока Given/Odesolve выглядит следующим образом:
79
f 1(t):= |
f 2(t):= |
f 3(t):= |
x0:= |
y0:= |
z0:= |
t0:= |
T := |
|
Given |
|
|
f 1(t) =0 |
f 2(t) =0 |
f 3(t) =0 |
x(t0) = x0 y(t0) = y0 z(t0) = z0
x |
x |
|
||
|
|
|
|
|
y |
=Odesolve y |
, t, T |
||
|
|
|
|
|
z |
z |
|
||
Вместо многоточий необходимо поставить конкретные значения правых частей функций или переменных величин. В результате мы получаем решение в виде вектор-функции.
В качестве конкретного примера рассмотрим решение предыдущей задачи о колебаниях в виде системы двух уравнений первого порядка. Для этого введем две функции: y1(t) =y(t) – переме-
щение материальной точки, и y2(t) =y′(t) – скорости этой же точки. В этом случае программа будет иметь следующий вид:
Можно вывести графики для перемещений y1(t) и скоростей
y2(t) точки в зависимости от вре-
мени. График перемещения совпадает с предыдущим решением.
Кроме вычислительного блока
Given/Odesolve, в Mathcad
встроены еще три функции, которые позволяют решать задачу
80
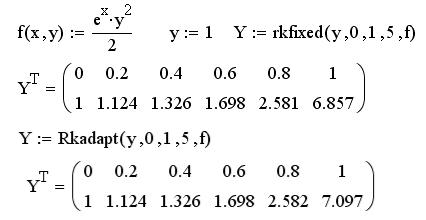
Коши для обыкновенных дифференциальных уравнений численными методами.
Y:=rkfixed(y0, a, b, N, F) – функция, решающая задачу Коши для уравнений первого порядка или систем n уравнений первого порядка, записанных в нормальном виде. Решение осуществляется методом Рунге–Кутта четвертого порядка.
Y:=Rkadapt(y0, a, b, N, F) – такая же функция как и rkfixed,
только решение производится с переменным шагом. Y:=Bulstoer(y0, a, b, N, D) – решение задачи Коши для уравнений первого порядка или систем n уравнений первого порядка, записанных в нормальном виде. Решение осуществляется методом Булирша–Штера.
Аргументы данных функций означают:
y0 – вектор начальных значений искомой функции в точке a.
a– левая граница области.
b– правая граница области.
N – число разбиений отрезка [a, b].
F – векторная функция, задающая правые части нормализованного уравнения или системы уравнений. Количество строк векторной функции совпадает с количеством уравнений.
Y – матрица, в нулевом столбце которой находятся координаты абсцисс, а в последующих столбцах выводится затабулированное решение задачи Коши. Так, для уравнения первого порядка матрица Y содержит два столбца, для системы двух уравнений первого порядка – три столбца, и так далее.
В качестве примера использования функции rkfixed и Rkadapt рассмотрим решение задачи Коши (5.2).
Сравнивая результаты работы функций rkfixed и Rkadapt, мы видим, что вторая функция дает более точные результаты.
81
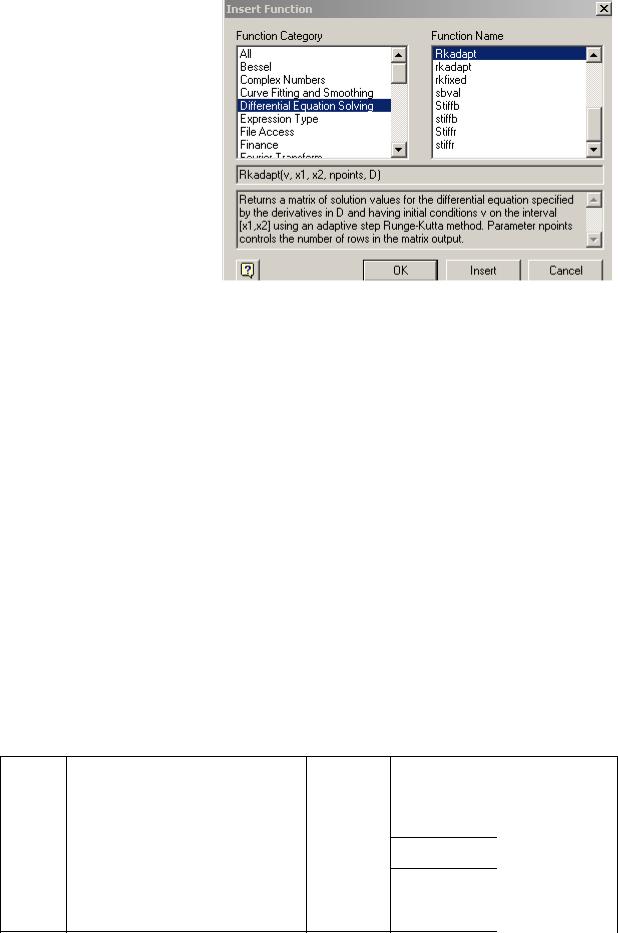
Кроме перечисленных функций, в Mathcad встроено еще более десяти функций, направленных на решение обыкновенных дифференциальных уравнений. Список всех функций с небольшим объемом справочной информации
можно посмотреть, нажав на кнопку  или Insert/Function.
или Insert/Function.
Без подробных комментариев, рассмотрим еще две функции, предназначенные для решения неустойчивых задач Коши или, так называемых «жестких» обыкновенных дифференциальных уравнений.
Y:= stiffb(y0, a, b, N, F, J) – решение жестких систем методом Булирша–Штера.
Y:= stiffr(y0, a, b, N, F, J) – решение жестких систем методом Розенброка.
Последним параметром данных функций является матрица J(t,y), составленная из якобиана (левые столбцы) и вектора производных по x (правый столбец). Примеры решения жестких систем выходят за рамки курса математики для инженерных специальностей.
Задание для самостоятельной работы
Решить задачу Коши, используя вычислительный блок
Given/Odesolve и функции rkfixed или Rkadapt.
№ Дифференциальное [a,b] Начальные условия Вар. уравнение
|
|
|
y/ (0) |
|
|
1 |
y// − y′+ xy2 = 0 |
[0,3] |
=1 |
y(0) =1 |
|
2 |
y// +0.2y/ + xy = 0 |
[0,20] |
y/ (0) |
= 0 |
y(0) =1 |
3 |
y// − x2 y/ = x4 y2 + xy |
[0; 1.5] |
y/ (0) |
=1 |
y/ (0) = 2 |
4 |
y// + 2xy/ − y = 0 |
[0,5] |
y/ (0) |
= 0 |
y(0) =1 |
82
5 |
y// + x3 y = y′ |
|
[0,3] |
||
6 |
y// +0.2y/ + xy = 0.3 |
[0,5] |
|||
7 |
y// + xy2 = y′ |
|
[0; 3] |
||
8 |
y// + x2 y/ |
= x |
|
[0,12] |
|
9 |
y// +3y/ + xy = 0 |
[0,12] |
|||
10 |
y// + y/ − xy = 0 |
[0,5] |
|||
11 |
y// +0.3xy/ |
=1 |
|
[0,5] |
|
12 |
xy// −0.3y/ |
+ x = 0 |
[1,4] |
||
13 |
y// −2xy = x |
|
[1,4] |
||
14 |
y// − xy/ = x2 |
|
[2,3] |
||
15 |
y// − x2 y/ |
= x2 y2 |
[0, 2] |
||
16 |
y// − x2 y/ |
+ 4y = x2 |
[0, 3] |
||
17 |
y/ +0.5x4 y// = x2 |
[1,2] |
|||
18 |
y// −0.1y/ +ex y = 0 |
[–2,4] |
|||
19 |
y// +(x +1) y/ = x |
[–1,3] |
|||
20 |
y// +(x + x2 ) y/ |
= x |
[0,2] |
||
21 |
y// −(x + x2 ) y/ |
= 0 |
[0,1] |
||
22 |
y// − y′+ xy3 = 0 |
[0,4] |
|||
23 |
y// +e3x y = x2 |
|
[0, 2] |
||
24 |
y// +0.2e2 x y = cos(x) |
[0,10] |
|||
25 |
y// + x2 y/ |
= cos(2x) |
[0,7] |
||
26 |
y// +cos(x) y/ = x2 |
[0,4] |
|||
27 |
y// +cos(x) y = x |
[0,4] |
|||
28 |
y// +sin2 (x) y + y/ = 0 |
[0,7] |
|||
29 |
y// −sin3 (x) y = y/ |
[0,3] |
|||
30 |
y// +(2x +3) y/ |
= 3x3 + 2 |
[0,4] |
||
y/ (0) = 0 y/ (0) = 4 y/ (0) =1 y/ (0) = 0 y/ (0) = 0 y/ (0) =1 y/ (0) = 0 y/ (0) =1 y/ (0) =1 y/ (0) = 0 y/ (0) =1 y/ (0) =1 y/ (0) = 0 y/ (0) =1 y/ (0) = 6 y/ (0) = 0 y/ (0) =1 y/ (0) =1 y/ (0) = 0 y/ (0) = 0 y/ (0) =1 y/ (0) =1 y/ (0) = 0 y/ (0) = 0 y/ (0) =1 y/ (0) =1
y(0) =1 y(0) = 2 y(0) =1 y(0) = −1 y(0) = −1 y(0) = 3 y(0) = 3 y(0) = 2 y(0) =1 y(0) = 3 y(0) = 0 y(0) =1 y(0) =1 y(0) = 2 y(0) =1 y(0) = 3 y(0) = 2 y(0) =1 y(0) = −1 y(0) = −1 y(0) = 3 y(0) = 3 y(0) = 3 y(0) = 3 y(0) = 2 y(0) =1
83
